| \(f(x)=\left\{\begin{array}{cl}A&\text{for } |x| \lt a\\0&\text{for} |x| \gt a\end{array}\right.\) |
 |
| \begin{eqnarray*} F(p)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-a}^a Ae^{-ipx}dx=\frac{A}{\sqrt{2\pi}}\frac{1}{-ip}\left[e^{-ipx}\right]_{-a}^a\\ F(p)&=&\frac{A}{\sqrt{2\pi}}\frac{2}{p}\underbrace{\frac{1}{2i}\left(e^{ipa}-e^{-ipa}\right)}_{\mbox{$\sin(pa)$}}=\frac{2aA}{\sqrt{2\pi}}\frac{\sin(pa)}{(pa)}\end{eqnarray*} |  |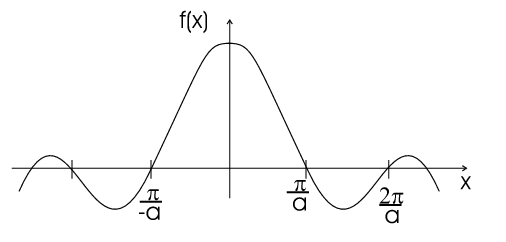
\begin{eqnarray*} f(x)&\stackrel{\alpha\gt0}{=}&e^{-\alpha|x|}\\ \rightarrow F(p)&=&\frac{1}{\sqrt{2\pi}}\left(\int\limits_0^\infty e^{-\alpha x}e^{-ipx}dx+\int\limits_{-\infty}^{0}e^{\alpha x}e^{-ipx}dx\right)\\ &=&\frac{1}{\sqrt{2\pi}}\left\{\left[\frac{1}{-(\alpha+ip)}e^{-(\alpha+ip)x}\right]_0^\infty+\left[\frac{1}{(\alpha-ip)}e^{(\alpha-ip)x}\right]_{-\infty}^0\right\}\\ &=&\frac{1}{\sqrt{2\pi}}\left(\frac{1}{\alpha-ip}+\frac{1}{\alpha+ip}\right)=\frac{1}{\sqrt{2\pi}}\frac{(\alpha+ip)+(\alpha-ip)}{\alpha^2+p^2}\\ \Rightarrow F(p)&=&\sqrt{\frac{2}{\pi}}\alpha\frac{1}{\alpha^2+p^2}\end{eqnarray*}
\begin{eqnarray*} f(x)&=&e^{-\frac{\alpha^2x^2}{2}}\;\rightarrow\,F(k)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}e^{-\frac{\alpha^2 x^2}{2}}e^{-ikx}dx\\ F(k)&=&\frac{1}{\alpha}e^{-\frac{k^2}{2\alpha^2}}\;\;\mbox{FT(Gaussian) is a Gaussian}\end{eqnarray*}
| \[f(t)=\left\{\begin{array}{cl}e^{-\alpha t}&\mbox{for $t\ge 0$}\\0&\mbox{for $t\lt0$}\end{array}\right.\] |
\begin{eqnarray*} F(\omega)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{0}^\infty e^{-\alpha t}e^{-i\omega t}dt=\frac{1}{\sqrt{2\pi}}\frac{1}{-\alpha-i\omega}\left[e^{-\alpha t-i\omega t}\right]_{0}^\infty\\ F(\omega)&=&\frac{1}{\sqrt{2\pi}}\frac{1}{\alpha+i\omega}\end{eqnarray*}
With frame
Fourier-Transformation: Definition