| Periodic functions: | 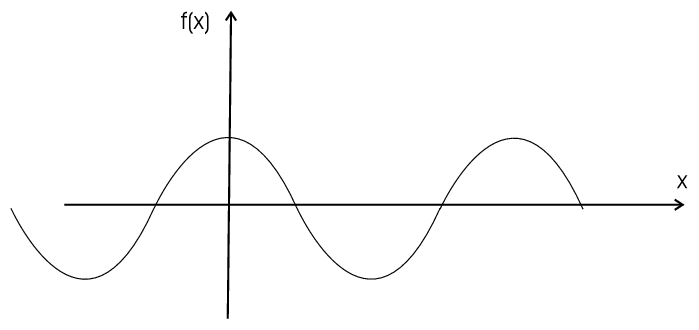
| \(f(x)=\sin x \qquad\) o.k. |
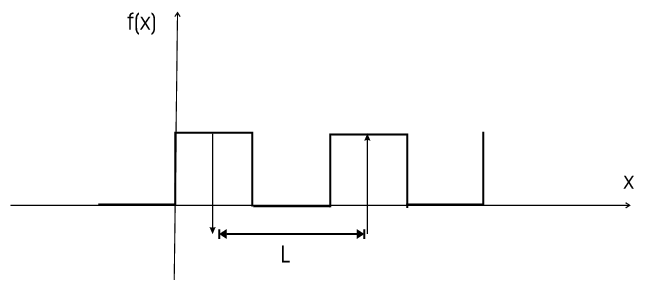 | 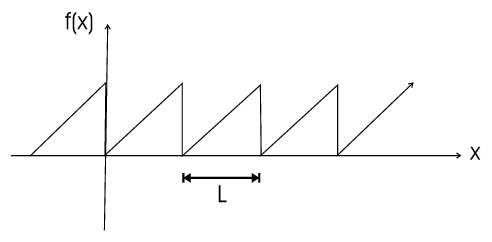 |
Definition 33 A function \(f(x)\) is called periodic if \(L\gt0\) exists with \(f(x)=f(x+L)\) for all \(x\). \(L\) is called the periodic of \(f\).
Example: \begin{eqnarray*}f(x)&=&\sin x\qquad L=2\pi\\ f(x)&=&\sin^2x\qquad L=\pi,\;\;\mbox{also:}\;\;f(x)=f(x+nL),\;n\in\mathbb{Z}\\ f(x)&=&\sin10x\;\rightarrow\quad L=\frac{2\pi}{10}\end{eqnarray*}
\(\Rightarrow\)
now we will see that \(\sin x\) and \(\cos x\) are prototypes of periodic functions.
If \(f\) has period \(L\) than \(F(x)=f(\frac{L}{2\pi}x)\) has the period \(2\pi\)
Example:
| \[ f(x)=\sin(10x)\;\rightarrow\;f(\frac{2\pi}{10 * 2\pi}x) = \sin x\;\;\mbox{period $2\pi$}\] |
| \[\Rightarrow\left|\begin{array}{l}\mbox{It is sufficient to investigate functions with period $2\pi$. Transformation $\frac{2\pi}{L}x$ will}\\ \mbox{give arbitrary period, i.e.\ $f(x)=F(\frac{2\pi}{L}L)$}\end{array}\right.\] |
| \[ \left.\begin{array}{lcl}\frac{1}{\pi}\int\limits_0^{2\pi}\sin(kx)\sin(nx) dx&=&\delta_{kn}\\ \frac{1}{\pi}\int\limits_0^{2\pi}\cos(kx)\cos(nx) dx&=&\delta_{kn}\\ \frac{1}{\pi}\int\limits_0^{2\pi}\cos(0 x)\cos(0 x) dx&=&2\\ \frac{1}{\pi}\int\limits_0^{2\pi}\sin(kx)\cos(nx) dx&=&0\end{array} \right\}k,n\in\mathbb{N}\quad\begin{array}{l}\mbox{important formulas, which show that }\\\mbox{$\sin$ and $\cos$ can be used as a ''base'' in a vector space}\end{array} \] |
\begin{eqnarray*}f(x)&=&\frac{a_0}{2}+\sum_{k=1}^\infty\left(a_k\cos(kx)+b_k\sin(kx)\right)\\ \mbox{with:}\quad a_0&=&\frac{1}{\pi}\int\limits_0^{2\pi}f(x) dx \quad \mbox{(2 $\times$ mean over period)},\\ a_k&=&\frac{1}{\pi}\int\limits_0^{2\pi}f(x)\cos(kx) dx,\\ b_k&=&\frac{1}{\pi}\int\limits_0^{2\pi}f(x)\sin(kx) dx,\end{eqnarray*}
is called the
Fourier-Series of a function \(f(x)\) with period \(2\pi\); \(a_k\) and \(b_k\) are called the Fourier coefficients of \(f(x)\)
Exploiting the symmetries of function one can considerably reduce the mathematical effort
for calculation Fourier coefficients:
since the periodicity length is \(2\pi\) \(f(-\pi +x) =f(\pi +x)\); so the limits in the integrals for the Fourier coefficients can always be changed to a
symmetrical representation, i.e.
| \[\int\limits_0^{2\pi} ... dx = \int\limits_{-\pi}^{\pi} ... dx\] |
Thus:
| \[ \begin{array}{lllcl} f(x) & = & -f(-x)\rightarrow\mbox{anti-symmetric} & \rightarrow & \mbox{cos-coeff. are zero!}\quad \int\limits_{-\pi}^{\pi}f(x)\cos(kx) dx=0\\ & & &\mbox{and}&\quad \int\limits_{-\pi}^{\pi}f(x)\sin(kx) dx = 2 \int\limits_0^{\pi}f(x)\sin(kx) dx\\ f(x)&=&f(-x)\rightarrow\mbox{symmetric}&\rightarrow&\mbox{sin-coeff. are zero!}\quad \int\limits_{-\pi}^{\pi}f(x)\sin(kx) dx=0\\ & & &\mbox{and}&\quad \int\limits_{-\pi}^{\pi}f(x)\cos(kx) dx = 2 \int\limits_0^{\pi}f(x)\cos(kx) dx \end{array} \] |
© J. Carstensen (Math for MS)