Fourier series in complex description

3.12 Fourier series in complex description

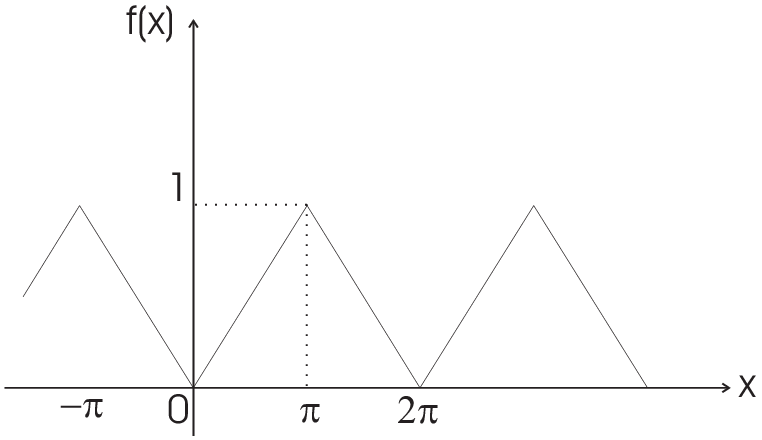\begin{eqnarray*}\cos x&=&\frac{1}{2}\left(e^{ix}+e^{-ix}\right) \qquad \sin x = \frac{1}{2i}\left(e^{ix}-e^{-ix}\right)\\ \mbox{Thus: }\quad f(x)&=&\frac{a_0}{2}+\sum_{k=1}^\infty\left(a_k\cos(kx)+b_k\sin(kx)\right)=\sum_{k=-\infty}^\infty c_ke^{ikx}\\ &&\mbox{please beware of the negative indices}\\ &&\mbox{with:}\;c_0=\frac{a_0}{2}\;\mbox{and }c_k=\frac{1}{2}\left(a_k-ib_k\right);\,c_{-k}=\frac{1}{2}\left(a_k+ib_k\right)\\ &&\mbox{and }c_k=\frac{1}{2\pi}\int\limits_0^{2\pi}f(x)e^{ikx} dx\left(=\frac{1}{2\pi}\int\limits_0^{2\pi}f(x)\cos(kx) dx-\frac{1}{2\pi}i\int\limits_0^{2\pi}f(x)\sin(kx) dx\right)\\ &&\mbox{for $k=0,\pm1,\pm2,\pm3,\ldots$} \end{eqnarray*}

$c_k$ are the complex Fourier coefficients of $f(x)$ $\Rightarrow$ more compact treatment possible. As example:

$f(x)=\left\{\begin{array}{ccl}\frac{x}{\pi}&\mbox{for}&0\le x\lt\pi\\\frac{2\pi-x}{\pi}&\mbox{for}&\pi\le x\lt2\pi\end{array}\right.\;$ periodic continuation

\begin{eqnarray*} c_k&=&\frac{1}{2\pi}\int\limits_0^{2\pi}f(x)e^{-ikx} dx=\frac{1}{2\pi}\left(\int\limits_0^\pi\frac{x}{\pi}e^{-ikx} dx+\int\limits_\pi^{2\pi}\frac{2\pi-x}{\pi}e^{-ikx} dx\right)\\ \mbox{Note:}\;\int xe^{-ikx}dx&=&\frac{1}{k^2}e^{-ikx}\left(ikx+1\right)+C =\frac{1}{2}x^2+C\\ \rightarrow\,c_0&=&\frac{1}{2\pi^2}\left(\frac{1}{2}\pi^2-\frac{1}{2}0^2+2\pi\pi-\left(\frac{1}{2}(2\pi)^2-\frac{1}{2}\pi^2\right)\right) = \frac{1}{2\pi^2}\pi^2=\frac{1}{2}\\ c_k&=&\frac{1}{2\pi^2}\left[\frac{1}{k^2}e^{-ik\pi}\left(ik\pi+1\right)-\frac{1}{k^2}-\frac{1}{k^2}e^{\overbrace{-i2\pi k}^{\mbox{\large 1}}}(ik2\pi+1) +\frac{1}{k^2}e^{-ik\pi}\left(ik\pi+1\right)\right.\\ &&\left.+\frac{2\pi}{-ik}\left(e^{-ik2\pi}-e^{-ik\pi}\right) \right]\\ &=&\frac{1}{2\pi^2k}\left[e^{-ik\pi}\left(i\pi+i\pi-2\pi i\right)+\frac{1}{k}e^{-ik\pi}\left(1+1\right)-\frac{2}{k}+\left(-2\pi i+2\pi i\right)\right]\\ &=&\frac{2}{2\pi^2k^2}\left((-1)^k-1\right)=\left\{\begin{array}{cl}0&\mbox{if $k$ even}\\\frac{2}{\pi^2k^2}&\mbox{if $k$ odd}\end{array}\right.\\ \rightarrow\,f(x)&=&\frac{1}{2}-\frac{2}{\pi^2}\sum_{k=-\infty}^\infty \frac{1}{(2k+1)^2}e^{i(2k+1)x} = \frac{1}{2}-\frac{4}{\pi^2}\left(\cos x+\frac{1}{3^2}\cos3x+\frac{1}{5^2}\cos 5x+\ldots\right)\\ \\ x=0\quad\rightarrow\quad f(0)&=&0=\frac{1}{2}-\frac{4}{\pi^2}\left(1+\frac{1}{3^2}+\frac{1}{5^2}+\ldots\right) \qquad \mbox{Thus:} \qquad\sum_{k=0}^\infty\frac{1}{(2k+1)^2}=\frac{\pi^2}{8} \end{eqnarray*}

$\Rightarrow$ Fourier series be used to calculate series in the above manner!

\[\mbox{Example is}\;\sum_{k=1}^\infty\frac{1}{k^6}=\frac{\pi^6}{945}\;\mbox{(Euler 18th century)}\]

Major application of Fourier series: Arbitrary periodic function$\rightarrow$ $\sin,\cos$!
In general:

\[f(x) = \sum_{n=-\infty}^\infty c_ke^{i\frac{2\pi}{L}nx}\quad\mbox{for period $L$} \quad c_n = \frac{1}{L}\int\limits_0^L f(x)e^{-i\frac{2\pi}{L}nx} dx\]

3.12.1 Example: Fourier-Series with larger periodicity length