| Periodic function \(f(x)=f(x+2l)\) period 2l |  |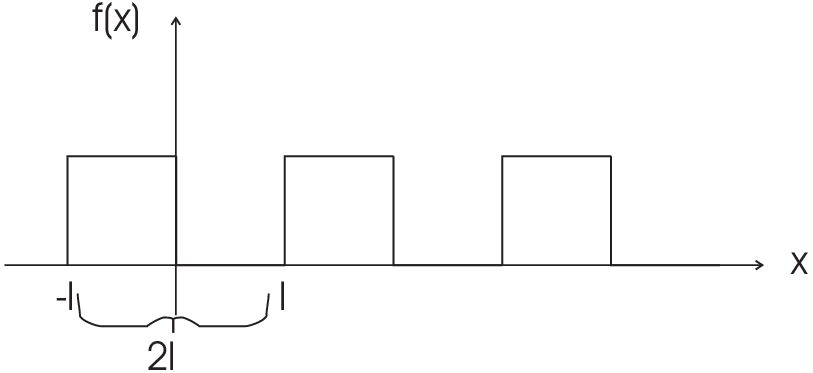
| Periodic function \(f(x)=f(x+2l)\) period 2l | |
| \[f(x) = \sum_{n=-\infty}^\infty F_ne^{ip_nx} \qquad p_n=n\frac{\pi}{l} \qquad F_n=\frac{1}{2l}\int\limits_{-l}^{+l}f(x)e^{-p_nx} dx \] |
 |
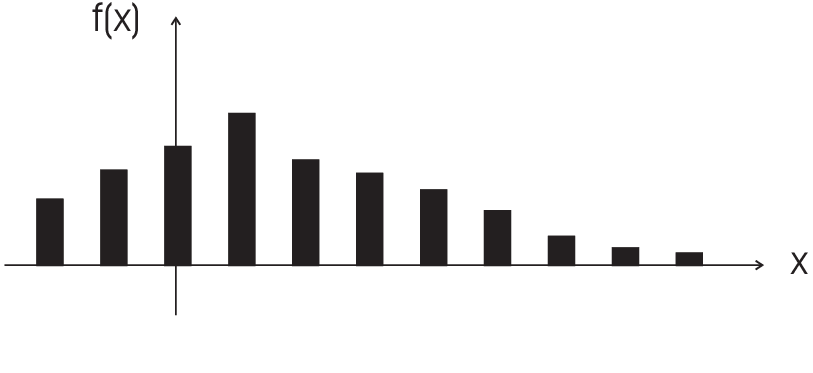\begin{eqnarray*}p_n&\Rightarrow&\text{periodic function} \quad \text{vs.} \quad \text{discrete spectrum}\\ \mbox{e.g.}\quad f(x)&=&\left\{\begin{array}{cl}-a&\mbox{for $-\pi \lt x \lt 0$}\\+a&\mbox{for $0\lt x \lt \pi$}\end{array}\right.l=\pi\\ \rightarrow\,f(x)&=&\frac{4a}{\pi}\left(\sin x+\frac{\sin3x}{3}+\frac{\sin5x}{5}+\ldots\right)\\ f_n&=&\left\{\begin{array}{cl}0&\mbox{ for $n$ even}\\\frac{4a}{\pi}\frac{1}{n}&\text{for } n \text{ odd}\end{array} \right. \end{eqnarray*}
Fourier series in complex description
© J. Carstensen (Math for MS)
With frame