Example: Positive part of sin function

3.11.2 Example: Positive part of sin function

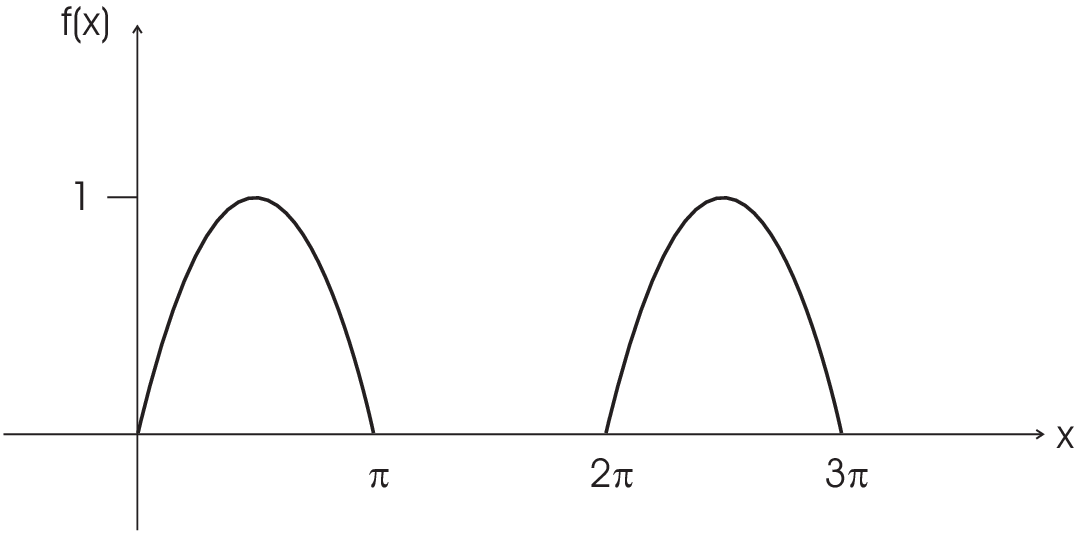$f(x)=\left\{\begin{array}{cl}\sin x&0\le x\lt\pi\\0&\pi\le x\lt2\pi\end{array}\right.\;\;\mbox{and periodic continuation}$

\begin{eqnarray*} \frac{a_0}{2}&=&\frac{1}{2\pi}\int\limits_0^\pi\sin x dx=\frac{1}{2\pi}\left[-\cos x\right]_0^\pi=\frac{1}{\pi}\\ a_k&=&\frac{1}{\pi}\int\limits_0^\pi\sin x\cos kx\;dx=\left\{\begin{array}{lcl}\frac{1}{\pi}\left[\frac{1}{2}\sin^2x\right]_0^\pi&=&0,\;\text{for}\;{k=1}\\ \frac{1}{\pi}\left[-\frac{\cos(1+k)x}{2(1+k)}-\frac{\cos(1-k)x}{2(1-k)}\right]_0^\pi&=&\left\{\begin{array}{cl}0&k\,\mbox{odd}\\\frac{1}{\pi}\frac{2}{1-k^2}&k\,\mbox{even}\end{array}\right.,\text{for}\;{k\gt1} \end{array}\right.\\\\ b_k&=&\frac{1}{\pi}\int\limits_0^\pi\sin x\sin kx\;dx=\left\{ \begin{array}{lclcl}\frac{1}{\pi}\left[\frac{1}{2}x-\frac{1}{4}\sin 2x\right]_0^\pi&=&\frac{1}{2}&\text{for}\;{k=1}\\ \frac{1}{\pi}\left[\frac{\sin(1-k)x}{2(1-k)}-\frac{\sin(1+k)x}{2(1+k)}\right]_0^\pi&=&0&\text{for}\;{k\gt1} \end{array} \right.\\ \\ \mbox{Thus:}\quad f(x)&=&\frac{1}{\pi}+\frac{1}{2}\sin x-\frac{2}{\pi}\sum_{k=1}^\infty\frac{1}{(4k^2-1)}\cos 2kx \quad \Rightarrow \quad \mbox{Due to $1/(4k^2-1)$ fast converging series} \end{eqnarray*}

To solve the above integrals we used relations extracted directly from the addition theorems for sin- and cos- functions:

\[\begin{array}{llll} &\sin(\alpha)\cos(\beta) &=& \frac{1}{2}\left(\sin(\alpha-\beta)+ \sin(\alpha+\beta) \right)\\\\ \Rightarrow & \sin(x)\cos(kx) & = & \frac{1}{2}\left(\sin((1-k)x)+ \sin((1+k)x) \right)\\\\ &\sin(\alpha)\sin(\beta) &=& \frac{1}{2}\left(\cos(\alpha-\beta)+ \cos(\alpha+\beta) \right)\\\\ \Rightarrow& \sin(x)\sin(kx) &=& \frac{1}{2}\left(\cos((1-k)x)+ \cos((1+k)x) \right) \end{array}\]

The following animation shows the Fourier-approximation for $f(x)=|\sin x|\quad$ up to 6.

With frame

Fourier series