Example: Periodic step function

3.11.1 Example: Periodic step function

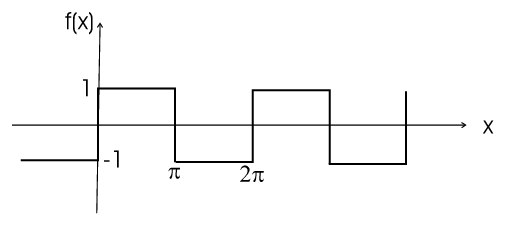$f(x)=\left\{\begin{array}{lcl}1&\mbox{if}&0\le x\le\pi\\-1&\mbox{if}&\pi\le x\le2\pi\end{array}\right.\;\;\mbox{and periodic continuation}$

Important note: \begin{eqnarray*} f(x)&=&-f(-x)\rightarrow\mbox{anti-symmetric}\rightarrow\mbox{cos-trans are zero!}\;\int\limits_0^{2\pi}f(x)\cos(kx) dx=0\\ b_k&=&\frac{1}{\pi}\int\limits_0^{2\pi}f(x)\sin(kx)dx=\frac{1}{\pi}\int\limits_0^{\pi}1\sin(kx)dx+\frac{1}{\pi}\int\limits_{\pi}^{2\pi}(-1)\sin(kx)dx\\ &=&\frac{1}{\pi}\left(\left.\frac{-\cos(kx)}{k}\right|_0^\pi-\left.\frac{-\cos(kx)}{k}\right|_\pi^{2\pi}\right)=\frac{1}{\pi k}\left(1-(-1)^k+1-(-1)^k\right)\\ &=&\frac{2}{\pi k}\left(1-(-1)^k\right)=\left\{\begin{array}{cl}0&\mbox{if $k$ even}\\\frac{4}{\pi k}&\mbox{if $k$ odd, $k=2n+1$}\end{array}\right.\\ \mbox{Thus:}\;f(x)&=&\frac{4}{\pi}\sum_{n=0}^\infty\frac{\sin(2n+1)x}{2n+1} =\frac{4}{\pi}\left(\sin x+\frac{\sin(3x)}{3}+\frac{\sin(5x)}{5}+\ldots\right) \end{eqnarray*}

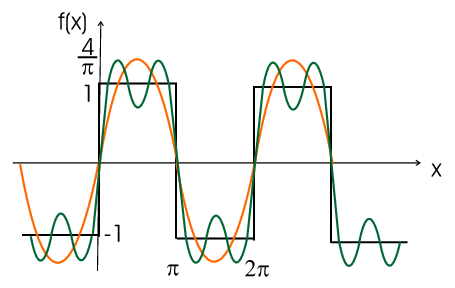$\rightarrow$ approximation by trigonometric functions
due to the factor $1/(2n+1)$ the series is slowly converging
(best with $n\to\infty$)

The following animation shows the Fourier-approximation for $f(x)=\left\{\begin{array}{cl}\sin x&0\le x\lt\pi\\0&\pi\le x\lt2\pi\end{array}\right.\;\;\mbox{and periodic continuation}$ up to 13.

With frame

Fourier series