 |
| geometrical definition of the scalar product |
The formal definition of a scalar product we already stated in definition 14. It holds for vectors with real and complex coefficients
as well as for functions interpreted as vectors (see section 3.8).
For an orthonormal set if base vectors \(\vec{e}_i\) and directly from
the representation of a complex number in the Riemann-plane using the definition 6, we get
| \[ \left\langle \vec{a}\right|\left.\vec{e}_i\right\rangle = a_i = \left|a\right|\; \cos\angle(\vec{a},\vec{e}_i), \] |
i.e. the scalar product between a vector \(\vec{a}\) and an orthonormal base vector \(\vec{e}_i\) calculates the projection of the vector \(\vec{a}\) in the direction of the base vector \(\vec{e}_i\). This is the most important property of the scalar product. Directly from this statement and the linearity of the scalar product we get
| \[\left\langle \vec{a}\right|\left.\vec{a}\right\rangle = \left|a\right|^2.\] |
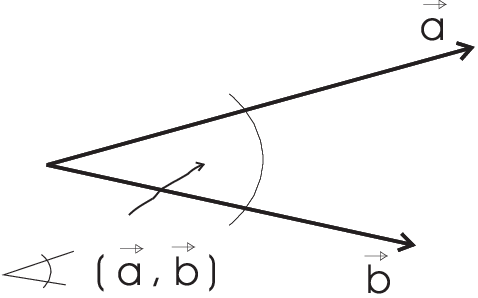
Example in 2D: \(\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2\) but also: \(\vec{a}\cdot\vec{b}=|\vec{a}|\;|\vec{b}|\cos\angle(\vec{a},\vec{b})\)
 |
| geometrical definition of the scalar product |
The scalar product can be interpreted as a special way of matrix multiplication: \begin{eqnarray*} \vec{a}^\top&\hat{=}&1\times N=\left(a_1,\ldots,a_N\right)\\ \vec{b}&\hat{=}&1\times N=\left(b_1,\ldots,b_N\right)^\top=\vec{b}\\ \vec{a}\cdot\vec{b}&=&\vec{a}^\top\vec{b}=\left(a_1,\ldots,a_N\right)\vect{b_1\\\vdots\\b_N}\hat{=}1\times 1 \quad. \end{eqnarray*}
This interpretation is especially useful for the generalization of the scalar product with complex coefficients:
| \[\vec{a}\cdot\vec{b}=\vec{a}^+\cdot\vec{b}=\overline{\vec{a}}^\top\,\vec{b}=\sum_{j=1}^N \bar{a}_jb_j\] |
Example:
| \[\begin{array}{ccc}\vec{a}&=&\vect{1\\i}\\\\\vec{b}&=&\vect{i\\i}\end{array}\rightarrow \quad \left\langle a \right|\left. b \right\rangle = \vec{a}\cdot\vec{b}=(1-i)\vect{i\\i}=+i+1\] |
© J. Carstensen (Math for MS)