 |
The vector product as an operator on two vectors is only defined 3D:
 |
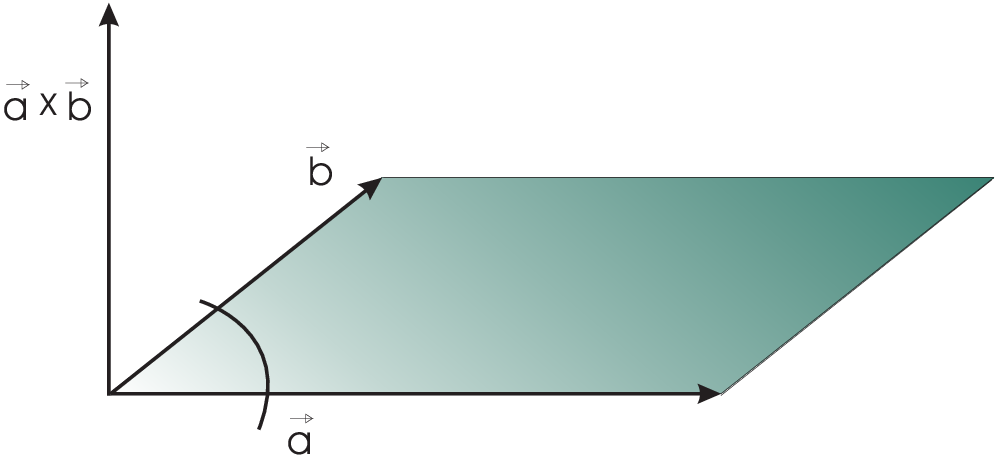
\(\vec{a},\vec{b}\,\in\mathbb{R}^3\,\rightarrow\,\vec{a}\times\vec{b}\)- vector which is
perpendicular to \(\vec{a}\) and \(\vec{b}\)
length is equal to the area of the parallelogram given by \(\vec{a}\) and \(\vec{b}\;\left|\vec{a}\times\vec{b}\right|=|\vec{a}|\,|\vec{b}|\sin\angle(\vec{a},\vec{b})\)
in components this means:
| \[ \vect{a_1\\a_2\\a_3}\times\vect{b_1\\b_2\\b_3}=\vect{a_2 b_3 - a_3 b_2\\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1}=\vec{a}\times\vec{b}\] |
The definition of the vector product using the properties of the determinant will here be discussed only for 3D (however this approach allows to generalize the vector product to all dimensions larger 1D):
| \[ \vec{e}_1=\vect{1\\0\\0}\quad\vec{e}_2=\vect{0\\1\\0}\quad\vec{e}_3=\vect{0\\0\\1}\] |
\begin{eqnarray*} \vec{a}\times\vec{b}&=&\left|\begin{array}{ccc}{\bf\vec{e}_1}&a_1&b_1\\{\bf\vec{e}_2}&a_2&b_2\\{\bf\vec{e}_3}&a_3&b_3\end{array}\right|\mbox{ the first ''{\bf bold}'' column represents the formal determinants}\\ &=&\vec{e}_1\left|\begin{array}{cc}a_2&b_2\\a_3&b_3\end{array}\right|-\vec{e}_2\left|\begin{array}{cc}a_1&b_1\\a_3&b_3\end{array}\right|+\vec{e}_3\left|\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right|\end{eqnarray*}
Note: \begin{eqnarray*}\vec{a}\times\vec{b}&=&-\vec{b}\times\vec{a}\\ \vec{a}\times\vec{a}&=&0\end{eqnarray*}
| \[\vec{a},\vec{b}\neq\vec{0}\quad\vec{a}\times\vec{b}=0\;\Leftrightarrow\;\mbox{$\vec{a},\vec{b}$ are linear dependent}\] |
Example:
| \[\vec{a}=\vect{1\\2\\3}\qquad\vec{b}=\vect{4\\5\\6} \quad \vec{a}\times\vec{b}=\vect{2\cdot6-3\cdot5\\3\cdot4-1\cdot6\\1\cdot5-2\cdot4}=\vect{-3\\6\\-3} \] |
Test:
| \[\begin{array}{lclcl}\vec{a}\cdot\left(\vec{a}\times\vec{b}\right)&=&-3+12-9&=&0\\ \vec{b}\cdot\left(\vec{a}\times\vec{b}\right)&=&-12+30-18&=&0\end{array}\rightarrow\;\begin{array}{lcl}\vec{a}&\bot&\vec{a}\times\vec{b}\\\vec{b}&\bot&\vec{a}\times\vec{b}\end{array}\] |
scalar+vector product: \begin{eqnarray*} \vec{a}\times\left(\vec{b}\times\vec{c}\right)&=&\vec{b}\left(\vec{a}\cdot\vec{c}\right)-\vec{c}\left(\vec{a}\cdot\vec{b}\right)\\ \vec{a}\cdot\left(\vec{b}\times \vec{c}\right)&=&\left|\begin{array}{ccc}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{array}\right|\hat{=}\,\mbox{Volume of }\end{eqnarray*}
So obviously the determinant of the 3 vectors (written as a \(3 \times 3\) matrix) calculates the volume spanned by the 3 vectors.
© J. Carstensen (Math for MS)