Maximum Impact Energy

How do we derive the maximum impact energy? To quote myself from the backbone: "Take the equations for the effective mass and multiply it with the equations for the velocity squared and you have (twice) the kinetic energy at the point x considered". So let's do that.

The effective mass m_eff merited its own science module. We can take the result right from there:

m_eff	=	m · I I + m · x²

The variable is x. In the positive direction we go along the blade, starting at the center of mass (COM). The mass of the sword is m, and I describes the moment of inertia for rotations around the center of mass perpendicular to the blade.
The coordinate system is important, it is shown below.


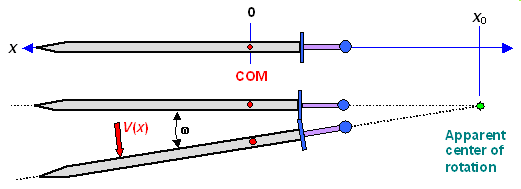Coordinates for calculating the maximum impact and assumed movement

We describe the motion of the sword by a rotation with a circular rotational velocity w around the apparent center of rotation at x₀. A point with coordinate x on the blade then has the velocity v(x) given by

v(x)	=	(x – x₀) · w

We need x minus x₀ because x₀ is a negative number in our coordinate system.
The kinetic energy of the blade at point x thus becomes

E_kin	= ½ ·	m_eff · v(x)²	= ½ ·	m · I I + m · x²	· (x – x₀)² · w²

Almost done. Just takes the derivative dE_kin/dx, set it equal to zero, and solve the resulting equation for x. That will yield x_P, the position of peak energy on the blade.
Try it. I tried and failed. You can easily get caught in lengthy equations if you don't do it the simple way that Jan Martin Wagner, a former coworker, showed me. Here goes:

First move the constants to the left of the equation, obtaining

2 E_kin w² m · I	=	(x – x₀)² I + m · x²	=	g(x) h(x)

We can express the functions as the quotient of two functions g(x) and h(x) which allows us to use the quotient rule for derivatives:

f(x)	=	g(x) h(x)

df(x) / dx	=	f'	=	h · g' – g · f' h'²

I now used the usual shorthand for functions and their derivatives. This will now give us

2 h'² w² m · I	dE_kin dx	=	h · g' – g · f'	= 0

	h · g'	=	g · f'

Now you see why the 2 h'² /w²m · I were moved to the left. They drop out as soon as we put the derivative of the energy to zero.
(For purists I hasten to point out that we need to check that h'² does not happen to be zero for the coordinate of the maximum, x_P, that we will obtain in order to avoid the forbidden division by zero)

It's easy now. We have

g(x)	=	(x – x₀)²		g'(x)	=	2(x – x₀)

h(x)	=	I + m · x²		h'(x)	=	2x

It follows

(I + m · x²) · 2(x – x₀)	=	2x · (x – x₀)²

x=x_P	=	– I / mx₀

	Surprise! The point of maximum impact is identical to the percussion point relative to the apparent center of rotation! It must have a negative sign because x₀ is negative in our coordinate system and the percussion point=point of maximum impact here, must be on the other side of the center of mass, i.e. on the positive part of the x-axis. Is the result a surprise? Hitting something with that percussion point produces no forces and torques at the center of apparent rotation, which means that you do not squander some of the available energy around the pivot point, allowing maximum force / torque / energy at the other end. Now a big question comes up. If we look at the apparent center of rotation given in the picture above, it corresponds to rotating the sword around your elbow or shoulder. The percussion point=point of maximum impact than is not far from the center of mass. Does that mean you should hit things close to the COM? No, it doesn't. For two reasons: In all these calculations we did not consider the weight of your arm. It is, after all, part of the moving masses. That would change all the number to some extent - but not too much. More important: If you hit something at the percussion point relative to a rotation axis going through your shoulder / elbow, you will deliver maximum impact and you won't feel forces and torques at your shoulder / elbow, indeed. But you will feel forces / torques at your wrist and since your wrist is far weaker than your elbow / shoulder, you now have a problem.
		It is far better to compromise and strike around the percussions point relative to a pivot point around your wrist, i.e. on the hilt. You deliver a bit less energy that way, but you will not damage yourself.