Magnetism

Elementary Stuff

Magnetism is not just about those magnets you use to fix the refrigerator art of you kids to the door of your refrigerator. Magnetism belongs to what we call the "electromagnetic" phenomena, and thus is always a part of whatever one associates with words like "electricity", "light" (more generally: "electromagnetic waves"), or "elementary particles".
In turn, words like "electricity" or "electromagnetic phenomena" are just expressions for: "things that electric charges can do" - just as expressions like "gravity", "weight" or "trajectories of cars, planets or satellites" refer to "things that gravitational charges can do". However, since most of us are lazy and traditionally minded, we never use the term "gravitational charge" but the simpler word "mass".

Remember that all things consist of some elementary particles (essentially electrons, protons, neutrons, the atoms they form, and photons). What "things" do depends on some basic properties of those particles. As far as the topic here is concerned, all we need to know about the properties of the everyday particles listed above is:

All particles have some always positive mass or "gravitational charge". That is even true for antiparticles that otherwise have typically properties opposite to those of their particles. Combinations of particles like atoms have the combined mass of their constituents. Masses come in all kinds of values.
Some particles have an electric charge , e.g. the electron and the proton. Charge always comes as either a positive or a negative elementary "monopole" charge of e = ± 1.602 · 10^–16 C. Some particles, e.g. the neutron, have no electric charge, antiparticles (like the positron) carry the opposite charge of the related particle. Combinations of particles like atoms have a total charge that is the sum of all the "inside" charges with the signs considered! A positive and a negative elementary charge thus sum up to zero.
Atoms, containing always the same number of electrons and protons thus are electrically neutral and have no net charge. Ions, i.e. atoms with missing or surplus electrons, have a few positive or negative elementary charges.
There is no such thing as a single magnetic charge or a magnetic monopole that elementary particles could carry around. Why? We don't know. It is not forbidden by the known laws of nature but magnetic monopoles seem not to exist.
There is, however, a property called "spin" that some elementary particles carry around in units of ±½ or ±1, and that is always associated with a magnetic dipole.
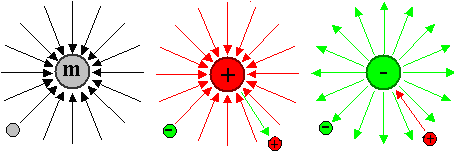
A particle with a mass and a charge produces a gravitational field and an electrical monopole field, that extends to "infinity". This field produces a force that acts on other particles with mass (all) or charge (some) that might be out there. This is illustrated below.


The basic monopoles and their fields.

On the left we have a particle with a mass. That could be any particle that can sit still, i.e. a neutron, an atom, an electron, and so on. The field is schematically represented by field lines that simply indicate the directions of the force that another particle with the proper "charge" - here simply mass - will experience. The force is always attractive in this case.
On the right we have particles with either a positive charge (e.g. a proton) or a negative charge (e.g. an electron). The field produced looks exactly the same as the gravitational field, but the forces can be attractive (between opposite charges) or repulsive (same charge) as shown. The magnitude of electrical forces between particle, however, is far larger (about a factor of 10⁴⁰) than the gravitational forces they experience.

Nothing like this exists for magnetism!

We have the monopoles covered. Now let's look at dipoles.
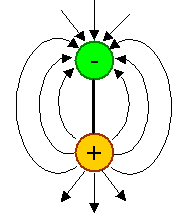
A dipole can be formed if a charge and an exact opposite charge is kept at a fixed distance. Since gravitational charges called "mass" only come with one sign, there can't be mass dipoles. We can easily make electrical dipoles, however:


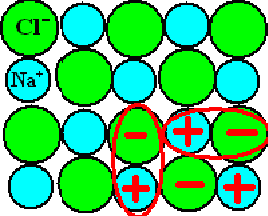
Basic electrical dipole with electrical field.	Electrical dipoles are everywhere, e.g. in ionic crystals like table salt (NaCl).
Electrical Dipoles

We now need to learn two basic truths about dipoles:

Electrical dipoles produce an electrical field that is well defined but quite different from the field of a monopole. The field lines, as always, indicate the force a (positive) "probe" charge would experience, and now it has a kind of direction.
Electric dipole fields are simply made by having "physical" dipoles consisting of two differently charged monopoles at a fixed distance as shown above. In stark contrast, magnetic dipoles can be made without having "physical" dipoles consisting of two different magnetic monopoles at a fixed distance. There are (so far) no magnetic monopoles, after all.

In fact, some elementary particles, while producing an electrical and gravitational monopole field due to their electrical and gravitational monopole charge, produce a magnetic dipole field despite the fact that there are no little magnetic monopoles inside.
Magnetically , an electron or proton looks like this:


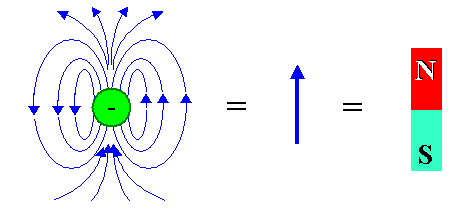Magnetic dipole field of a single electron and graphical abbreviations

A magnetic dipole field as shown is often "abbreviated" by a simple arrow or an elongated little magnet with a "north" and "south" pole. The electron in the figure above has also its usual electrical monopole field (not shown) around it, and its gravitational monopole field. The latter, however, is utterly unimportant and will never be mentioned again.
So let's commit to memory as a basic truth: Some elementary particles are intrinsic magnetic dipoles; it is an unalienable part of their existence.

Now we need to learn another basic truth about magnetic dipole fields:

Electrical charges moving in circles
produce a magnetic dipole field.

An electron moves if it goes from here to there. It may do so because it feels a force from some electrical field that happens to be around, but it may also move for different reasons. We have a special word for moving charges, we call that an electrical current.
If a hell of a lot of electrons move in a large circle, something we call: "a large current flowing through a coil", a big magnetic dipole field is generated that looks exactly like the field of a huge big magnetic dipole. We have made an electromagnet!
Inside an atom electrons also kind of move in a circle, and the very weak magnetic dipole fields produced in this way must be added to the magnetic dipole fields that the electrons carry around directly. Since quantum mechanics kicks in, the many little dipole arrows inside an atom cannot point in any directions but only "up" or "down". We add all these little "arrows" and the effects may exactly cancel: "up" + "down" = zero. The way the electrons arrange themselves inside atoms actually promotes cancellations, and many atoms have no net magnetic dipole field.

The long and short of this is that there are plenty of magnetic dipole moments inside atoms, and that after adding up, single atoms can have a permanent (small) magnetic dipole moment as we are going to call this dipole field from now on. That requires that all the little dipole moments of the electrons add up to something that is not zero. That must happen in all elements with an odd number of electrons because an "up" dipole can be perfectly canceled by a "down" one. For an even number of electrons cancellation is possible and happens for most (but not all) of those atoms and you get nothing.

Atoms thus either have some magnetic dipole field, or they don't. The question is: how can we tell? The answer is: Same as with electrical or gravitational fields. Wherever there is a magnetic field of whatever shape, there is a force on particles with a magnetic dipole moment. The dipole feels a force that tries to move it along the field lines and in addition - and that is new - a momentum that tries to rotate the dipole in such a way that its little magnetic arrow points in the direction of the field line arrow.

By now you are probably about to exclaim: "Much ado about nothing! I know that some piece of material is magnetic if it sticks to a magnet. I use magnets all the time when I put up refrigerator art from the kids".

I don't mind you quoting Shakespeare at me, but now tell me what, exactly, constitutes a magnet? Can you, personally, make one "from scratch" meaning from a bunch of suitable atoms? Very few people - and that includes scientists - could answer this question or pick the right kinds of atoms after just thinking hard for a while.
Let's see why "making" a magnet is a difficult conceptual enterprise:

Typical magnets are solids. Some solids are crystals, and that's what we are going to consider. There are non-crystalline magnets too, but let's keep this simple. Let's keep it as simple as possible. Let's first consider only elemental crystals that are made from one kind of atom.
The atoms of all elements either have
1. a magnetic moment (schematically shown like this: ) or
2. they don't: .
That give us two basic possibilities for making a crystal:
1. the crystal will either be completely unmagnetic or
2. it won't.
In the second case, we have once more two basic possibilities.
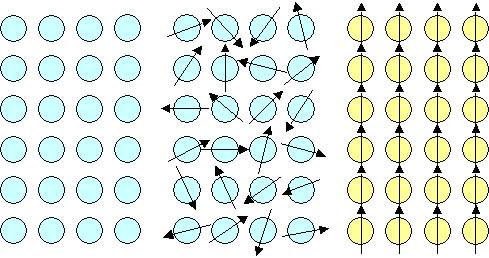
1. The magnetic moments of the atoms are not correlated at all, meaning that they point in random directions, or
2. they are correlated. There is some structure in the arrangement of the little arrows.
In the latter case we have several possibilities, for example:
1. all moments point in the same directions: ÝÝÝÝ... ,
2.: Moments point alternately up and down: ÝßÝß...

Let's illustrate this and find good names for the various phenomena.

Diamagnetic Material	Paramagnetic Material	Ferromagnetic Material

The three types of magnetic materials

Easy and self-explaining. Diamagnetic materials are simply not magnetic at all, meaning they cannot produce any magnetic fields. Paramagnetic materials produce tiny little dipole fields on atomic dimensions but since they are distributed randomly, adding them up gives zero on somewhat larger dimensions. Only in ferromagnetic materials as drawn above will the tiny little dipole fields of the individual atoms add up to a big strong dipole field of the crystal - we would get a magnet with a magnetic north and south pole.
The obvious question now is: Which elements are what? Looking not too closely and at room temperature, there is an easy answer:

About half of all elements are diamagnetic - essentially most (but not all) with an even numbers of electrons.
The remaining half is mostly paramagnetic.
The ferromagnetic minority consists of: iron (Fe), nickel (Ni) and cobalt (Co).

Looking a bit more closely, things get way more complicated. I'll give you a few points:

At lower temperatures more elements become ferromagnetic, e.g. gadolinium (Gd) below 289 K ( 16^oC, 61^oF), dysprosium (Dy) below 85 K (-188^oC, -306^oF ^o, or holmium (Ho) below 20 K (-253^oC, -423^oF). At high enough temperatures, all ferromagnetic elements (and compounds) become paramagnets.
Some elements don't have their magnetic moments arranged at random but in some well defined structure like ÝßÝß as pointed out above and thus appear to be unmagnetic. Chromium (Cr) is an example for what we call anti-ferromagnets, or manganese (Mn) at low temperatures.
Some elements that are paramagnetic as elemental crystal, happily subject their magnetic moments to some order if put in some compound. That's why compounds like chromiumoxide (CrO₂) are ferromagnetic, even so their constituents are not, and why weird stuff like cobalt-samarium (CoSm) or neodymium-iron-boron (Nd₂Fe₁₄B) makes stronger magnets than their ferromagnetic element by itself.

Now that we have fancy Latin names for the three basic magnetic types, and some idea of what's going on magnetically in the periodic table, we feel much better, and are now ready to tackle the tough question:

How come? Why do just a few elements align their magnetic moments when forming a crystal while most do not?
How come that all pieces of iron (or more generally: all ferromagnetic materials) get attracted by a magnet but are not necessarily magnets themselves?
What happens if you put those materials into a magnetic field? For example the magnetic dipole field that a big electromagnet can produce? Or just the magnetic field we find around the poles of a some magnet that we have around?
How does all of that depend on temperature? And why?

Looking into this in some detail would require an advanced lecture course in physics or Materials Science. In what follows I will therefore cover only a few essentials.

	1. How Come?
	Why do iron atoms in a bcc crystals align their magnetic moments in the same directions (Ý ÝÝÝ), producing ferromagnetic order, while quite similar other elements don't care? And why do they refuse to do that when you force them to make a fcc crystal? Why does chromium pick the anti-ferromagnetic order (ÝßÝ ß), and so on? There is a simple and an supremely difficult part to those questions.
		The simple part goes first. Obviously, if the magnetic moments of neighboring atoms align (or anti-align) themselves, they must "feel" each other. There must be an interaction, a force, an energy between those moments that is strong enough to compete with whatever mechanisms try to destroy order. This force obviously depends sensitively on parameters because it - obviously - is rather strong for iron atoms in a bcc lattice and rather weak for iron atoms in a fcc lattice, rather strong for cobalt atoms but rather weak for copper atoms, and so on. Sometimes this interaction wins, but mostly it looses.
		The difficult part is to write down proper equations for this interaction force, and then to solve these equations. We must delve rather deeply into more involved quantum theory to do this. Scientists have been doing this for many years by now, and quite a number of high-powered guys are doing this right now. A lot was achieved - but nobody at present can really make a ferromagnetic material from scratch, meaning calculating all its properties knowing only that it is iron or cobalt.
	When we extend this to compounds, alloys, amorphous materials, nanostuff, and so on, we are talking about one of the larger and flourishing research fields we have right now in physics or Materials Science. And that is all I'm going to say to question No 1.

2. What Makes a Magnet?

Some pieces of iron or of any ferromagnetic materials are strong magnets, some are not. How come?
Let's look at what we mean by the word "magnet" first.

A material-based magnet, or a bit more precisely, a permanent magnet, is a piece of material that always attracts ferromagnetic materials that are not magnets themselves, and attracts or repulses other magnets.

A magnet, in other words, is simply some ferromagnetic material that has a sizeable magnetic dipole field around itself. We can make that field "visible" by having small ferromagnetic particles around (simply iron filings, for example) that we disperse on a glass plate above a magnet. The filings orient themselves in the field of the magnet, and if we do it right, friction will prevent them from moving close to the poles of the magnet. What we get looks like this:


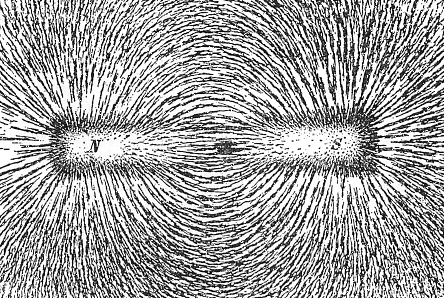The magnetic field around a permanent magnet
Source: Wikipedia commons

And here you have the reason why all ferromagnetic materials do their best not to be a magnet.

If you are a magnet, you fill the space around you with a magnetic dipole field and that field, like all fields, contains energy. Quite a lot, actually. That goes straight against the second law that states in no uncertain terms that you must minimize your free energy. Since magnetic fields are also orderly things, it doesn't help to invoke entropy, The simple truth is

You can't have a big magnetic field
and experience nirvana!

On the other hand, the very fact that we discuss ferromagnets here means that in the quest for nirvana, alignments of magnetic moments at the atomic level is good. It lowers the energy of the interaction between the atoms and low energy is a pre-requisite for nirvana. But alignment of the dipoles for many atoms creates that big external field with lots of energy that is bad for nirvana... Help!

Can you help those ferromagnetic crystals that want to be orderly but have to pay a high prize for it? I doubt it. But they don't need you help, they know what to do: Compromise!
Be orderly - but not in the same way everywhere. Don't do like shown in the left-had side of the figure below, but in a smarter way:


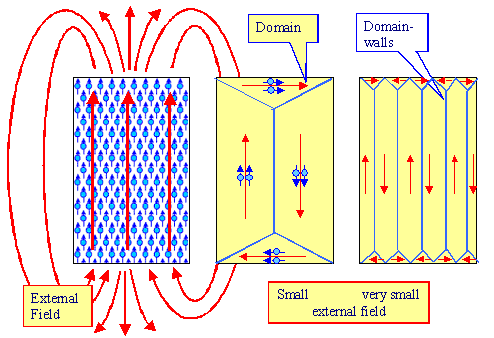Magnetic domains and external fields

Magnetic domains are formed. In well-defined regions of the crystals the magnetic momentums of the atoms are all aligned in the same direction (usually a prominent crystal direction, called an "easy" direction); in other regions they point in some other directions as shown above. If done smartly (right side of the figure above), the rather big magnetic fields of those magnetic domains overlap in such a way that they essentially cancel each other outside the crystal. In other words, summing up the the red arrows above that we will call magnetization vectors of the domains, gives a net magnetization of the crystal close to zero.
Of course, the first law of economics must not be denied either, so there is a price to pay. Between the domains are what's called domain walls, thin regions where the alignment is out of whack, and that costs some energy.

The crystal must do a tricky optimization job. It wants alignments of the magnetic moments, as much as possible, but needs to avoid external fields. That calls for lots of domain (far right in the figure above) - but this costs dearly in terms of domain walls. Moreover, in different crystal grains the "easy" directions are different, and that needs to be accounted for.
There is much more to consider but that is beyond your ken, dear reader. Actually, considering everything and then coming up with the best possible domain structure, is even beyond our ken. Even Materials Scientists cannot calculate the optimum domain structure at present.

Funny enough, our ferromagnetic crystals don't have that problems. They just make the best possible domain structures. Here are some examples of what you observe in reality:


Magnetic domains and external fields

The arrows were drawn in and show the direction of the field.. Otherwise: different shades / colors = different orientations.
Those magnetic materials produce amazing to outright beautiful structures! By the way, if you think that the inability to calculate those structures in details reflects badly on our mathematical prowess, think again. All I'm going to say is that you will encounter functions that mathematicians, for good reasons, call diabolical functions, with various degrees of diabolicity.

Whatever the domain structure looks like in detail, the effect is always that the material has no magnetic field on the outside and thus is not a "permanent magnet"!

So why is it attracted by a magnet?

Ferromagnetic Materials in a Magnetic Field

Let's put a ferromagnetic material that is not a permanent magnet because of its domain structure into a magnetic field. We do that, for example, by putting the material inside a coil. A current running through the coil produces a magnetic field inside the coil, and if we crank up the current, the strength of the magnetic field increases. The crystal responds and what we measure is the magnetization M of the crystal, the total effect of the alignment of the magnetic moments. It is close to zero in the beginning because of its the domain structure.

What we will get as a result looks like that:


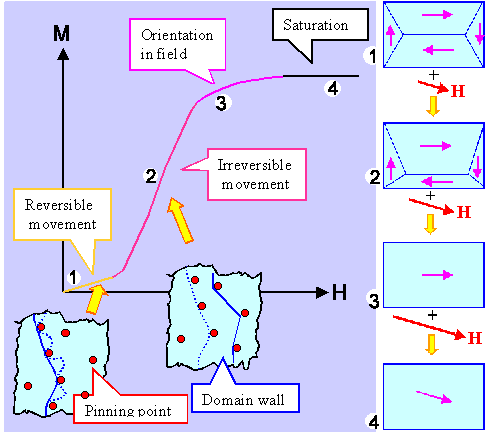Magnetization in external magnetic fields

A rather rich picture. What does it show? Let's look at it like 1, 2, 3, ..

The magnetic field inside some of the domains will happen to be more or less in the direction of the outside field, in other domains it is more or less the opposite. That's too bad because the energy of those unfavorably oriented domains goes up, while the energy of the favorably oriented ones goes down. The crystal, as always, tries to minimize its (free) energy, and the way to do that is obviously to make the favorably oriented domains bigger and the other smaller. That is shown on the right in the figures 1 and 2.
If some domains get bigger and others get smaller, the balance of the field can no longer result in zero but must give some finite magnetization M as shown in the graph of M versus the magnetic field strength H.
If domain sizes change, domain walls need to move. It is exactly like grain growth in crystals: :if grains are to grow bigger or smaller, grain boundaries need to move. In both cases, this is not easy. Magnetic domain walls, in particular might get "pinned" by all kinds of defects and get stuck, For unsticking them, you need to increase the "driving force" i.e. the external magnetic field. That's what the two insets try to show.
Eventually, for some large magnetic fields H, only one domain will be left. Its magnetization will still be in the easy crystallographic directions close but not identical to the direction of the external field. If you increase the field even more, the magnetization inside the domain eventually turns into the direction of the external field.
And that is the end. You cannot increase the magnetization after that any more, you have reached saturation. The value for saturation is tied to a material property called magnetic "permeability".

Here is what it really looks like:


Movement of domains in magnetic fields.
Source. Very old text book stuff. Sorry, forgot details

Saturation, by the way, occurs very roughly at a field strength around 1 Tesla for the best magnetic materials we have. "Tesla" is a weird and stupid unit for the strength of magnets; it replaced the sensible and dignified "Gauss". If you know anything about the guys with these names, you get my point.
Anyway, now you know why it is extremely difficult to go beyond 1 Tesla in technology. Materials can't help anymore. Only brute force, meaning enormous electrical currents, will do the job. If you want to go into high magnetic field research, you better buy yourself a sizeable power plant first.

The fun starts when we run our experiment backwards. After we reached saturation of the material we start to decrease the field by cranking the current down. What we will get looks like this:


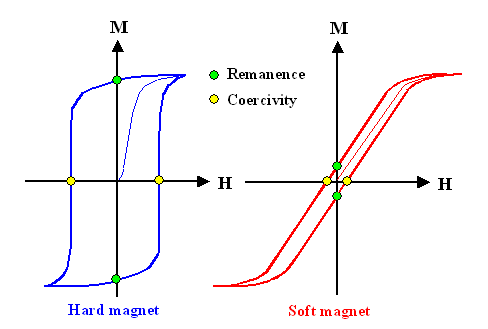Hystereses loops

We do not simply run down the same curve we produced running "up" (the virginal curve, shown in thin lines above) but run "in circles" or in a hystereses loop as it is called. The reason for this is simple:

Running up the magnetic field moved domain walls, but ever so reluctantly. Only because increasing the field increased the force on those walls, did they condescend to move on a bit. Now you decrease the field. The domain walls move back to some extent but then gets stuck. You decrease the field even more - and they will stay stuck!
That describes roughly the behavior of the blue curve that is typical for what we call "hard magnetic materials". When the field is reduced to zero, there is still a lot of magnetization in the material, described as the "remanence" of the material. You need to apply a sizeable magnetic field in the opposite direction to get those domain walls to move back to the original position with a zero magnetization of the material. The strength of this magnetic field we call the coercity of the material.
You realize, of course, that I just gave you the recipe for making a permanent magnet: get a hard magnetic material. Stick it into a coil and run up the current until you get saturation. Switch of the current, take your material out: it's a permanent magnet now - with a strength given by the remanence of the material you picked.

Soft magnetic material have little remanence and coercity an thus are not good for permanent magnets.
Of course, the obvious question now is: what makes magnetic materials "soft" or "hard"? The obvious answer is: in soft magnetic material , domain wall can be moved rather easily, in contrast to hard magnetic materials. The real question thus is: What, exactly, determines how easy or difficult it is to move a domain wall? Or, to put the question another way: how can I magnetically harden or soften my material ?

You guessed it. By optimizing the kind of material you use (don't just take some iron, alloy it with this and that!) and then doing some defect engineering (small / large grains, precipitates dislocations, ...)

The basic principles are rather similar to what we do for hardening iron / steel mechanically . We are simply talking basic Materials Science and Engineering principles here.

Back to magnetic materials. Let's just look ever so cursorily at what one does with magnetic stuff. I'll give you two lists - one for soft, and one for hard magnets

Basic uses of hard magnets:

Permanent magnets. From weak magnets for putting art on the refrigerator, to extremely strong iron-neodymium-boron magnets inside small (your bicycle dynamo) and big (wind mill) generators.
Data storage. From the good old magnetic tapes to the tera byte hard drive on your computer. The thin magnetic layers that store the one's and zero's as "up" or "down" magnetization in some small area need to be made from "hard" magnetic material.

Basic uses of soft magnets:

Transformer cores. You want the magnetization to follow as exactly as possible the alternating current in the first coil, so it can induce the same alternating current in the second coil.
Electromagnet cores. You want to strengthen the field that the current makes with the field coming from the material in the coil, but you also want it to disappear if you turn off the current
Magnetic shielding. Wrap a soft magnetic material around whatever you want to be magnetically shielded. For example magnetic resonance tomography machines.

How About Temperature?

Imagine all the magnetic moments of the atoms in a ferromagnetic material to be nicely aligned at room temperature. The atoms do that because that lowers the energy, or more precisely, the enthalpy of the system by some DH_order. It's good for nirvana.
Now heat up the material to a temperature T.

Perfect alignments means perfect order and therefore zero entropy S. That's fine at low temperature, including possibly room temperature, because the entropic part TS of the free enthalpy G would be small even if there would be disorder.
At higher temperatures, however, it simply doesn't pay anymore to save some energy DH_order, if TS_disorder would be larger, i.e. G = H – TS would be smaller for disorder.

So for exactly the same reason why an ordered arrangement of atoms (called solid crystal) gives way to a disordered arrangement (called liquid ) at some special temperature called "melting point", ferromagnetic ordering of magnetic moments gives way to paramagnetic disorder at a special temperature called Curie temperature.

Loosing magnetic order is a gradual process. The perfection of the alignments and thus the magnitude of the resulting magnetization decreases with increasing temperature. At the Curie temperature the distribution of the atomic magnetic moments is completely random and the magnetization zero. This is shown below


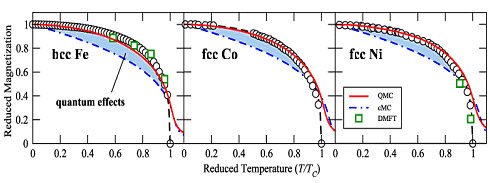Magnetization vs. temperature for the three elemental ferromagnetic materials iron (Fe), nickel (Ni) and cobalt (Co).
Soure: T. Hickel. B. Grabowski, F. Körmann, J. Neugebauer: Advancing density functional theory to finite temperatures: methods and applications in steel design, J. Phys.: Condens. matter 24 (2012) p. 1 - 17

The circles show experimental data. The red curves and the green squares were calculated with the presently best theories: QMC" for "quantum Monte Carlo" and IMFT for "dynamical mean-field theory". cMC stands for the older "classical Monte Carlo" routine.

I like to make two points to these diagrams

1. The saturation magnetization M_sat and the Curie point temperatures T_Curie for the three metals shown above are quite different. But if you plot with "reduced" quantities (M/M_sat and T/T_Curie), they are very similar. This simply shows that the underlying mechanism is the same.

2. All three theories are rather sophisticated and need big computers to produce results. While the "classical" Monte Carlo approach produces a curve that is not too close to the measured ones, the more sophisticated theories are getting there. The difference is simply raw computer power. One thing, however, is obvious: