5.4.2 Dislocation Reactions Involving Partial Dislocations

Splitting of perfect dislocations and some reactions

hierzu: siehe auch englisches Skript!
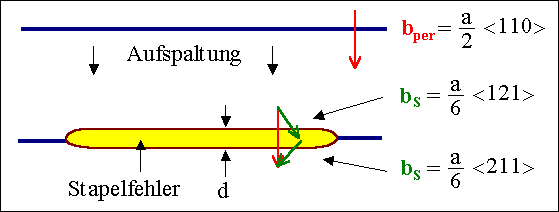
	Eine sog. "perfekte" Versetzung mit b=a/2 <110> kann in zwei Shockley-Partialversetzungen aufspalten und dabei Energie gewinnen. Dabei wird natürlich ein Stapelfehler gebildet. Die beiden Teilversetzungen werden sich soweit voneinander entfernen, bis Gleichgewicht zwischen dem Energiegewinn durch großen Abstand und dem Energieverlust durch Aufspannen eines Stapelfehlers vorliegt.
	Energiebilanz: Energie der Versetzung: Energiegewinn durch Aufspaltung: Vorher: Energie ist proportional zu 2a2/4=a2/2 Nachher: Energie ist proportional zu 2 (6a2/36)=a2/3 Entfernung d:   Zusatzenergie ist proportional zu 1/d Stapelfehler:  Zusatzenergie ist proportional d Konsequenz:  Es existiert ein Gleichgewichtsabstand dGG=dGG(g) mit g=Stapelfehlerenergie (pro cm2)
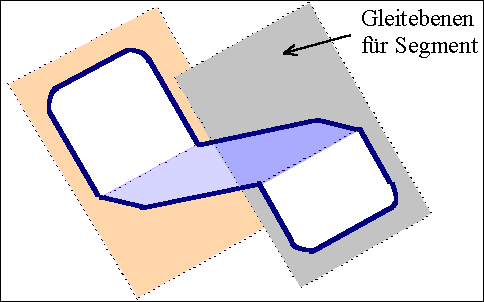
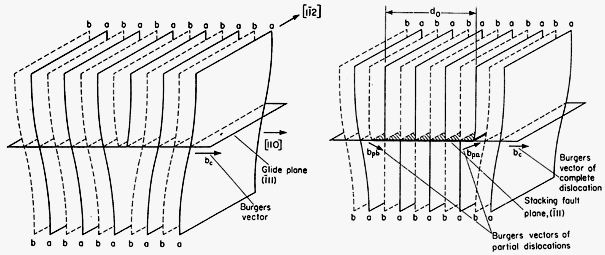
	Abbildung:Perspektivzeichnung einer aufgespaltenen Versetzung
		Es ist unmittelbar klar, daß die aufgespaltene Versetzung mit "Shockley-Partials" nach wie vor gleitfähig ist (der Stapelfehler läuft mit), während Frank Versetzungen nur beschränkt beweglich sind (auf einem Gleitzylinder) und insbesondere ihre Länge nur durch Klettern verändern können.
	Versetzungsreaktionen werden jetzt richtig spannend.
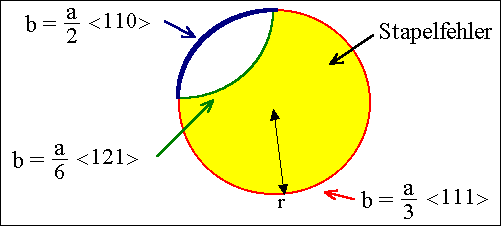
		Zum Beispiel kann aus einem durch Leerstellenagglomeration gebildeten Versetzungsring ("Frank-Ring) mit (Partial)-Burgersvektor a/3 <111> durch Aufspaltung der Frank-Versetzung in eine perfekte Versetzung plus eine Shockley- Versetzung mit anschließendem Durchgang der Schockley-Versetzung durch den Ring, ein Versetzungsring mit perfektem Burgersvektor werden - es besteht dann volle Gleitfähigkeit; der Ring wirkt als Versetzungsquelle. Treibende Kraft ist die mit wachsendem Ringdurchmesser zu groß werdende Stapelfehler-Energie (Wächst mit r2, während die Versetzungsenergie nur mit r wächst). Ist die Shockley-Versetzung ganz durchgelaufen ("gezogen" vom Stapelfehler; wirkt wie ein gespanntes "Gummituch"), liegt ein perfekter Versetzungsring vor. Das Peierls Potential sorgt dafür, daß sich Segmente der Versetzung in <100> Richtungen legen. Alle Segmente sind gleitfähig; liegen Spannungen vor, werden Segmente mit der höchsten Spannungskomponente auf der Gleitebene sich bewegen und lange Versetzungsdipole ausziehen.
	Abbildung: Beispiele für obige Prozesse in Silizium
DerThompson Tetraeder
	Die Geometrien werden selbst im einfachen face-centered cubic - Gitter etwas unübersichtlich. Das wichtigste Hilfsmittel um bei Indizierung und Reaktionen keinen Fehler zu machen, ist der Thompson Tetraeder, d.h. der durchgehend richtig indizierte Tetraeder aus den {111}-Ebenen des face-centered cubic Kristalls.
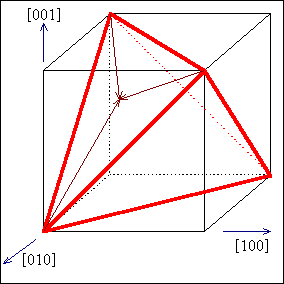		Betrachtet man nur den Tetraeder, kann man folgende Zusammenhänge erkennen: - Die Seiten liegen in <110>- Richtungen, sie repräsentieren die Burgersvektoren der vollständigen Versetzungen und die bevorzugte Linienrichtung in face-centered cubic Kristallen. - Die Flächen sind {111} - Flächen, sie zeigen die Lage der möglichen Stapelfehler. - Die Shockley-Partialversetzungen, die einen Stapelfehler auf einer gegebenen 111 - Ebene beranden, sind die Vektoren, die vom Mittelpunkt eines 111 - Dreiecks zu den Ecken laufen.
		Für eine "Steno"beschreibung benennt man die Ecken mit A,B,C, und D; die Flächenmitten mit a, b, g und d. Die Vektoren werden dann als z.B. AB ode Ag bezeichnet.
		Abbildung: Netz für Thompson Tetraeder