5.4 Partialversetzungen und Stapelfehler

5.4.1 Stapelfehler in dichtesten Kugelpackungen

hierzu: siehe auch englisches Skript!
	Ausgangspunkt ist die dichteste Kugelpackung in der Ebene
		Folie und Tischtennisball-Modell
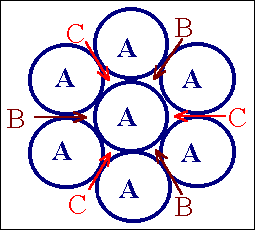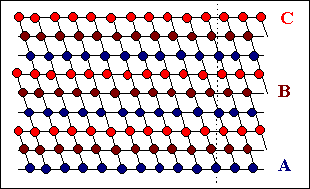
		Die blauen Kreise symbolisieren Atome in der "A - Lage"; die nächste Lage kann entweder eine "B-" oder eine "C - Lage" sein. Wählt man "B", dann wird die dritte Lage entweder wieder "A" oder "C" - wir erhalten das hexagonale oder das flächenzentrierte Gitter.
	Die Stapelfolgen ist daher:
		im fcc- Gitter: ABCABCABCA...
		im hexagonalen Gitter ist: ABABABA...
	In einer Seitenansicht sieht das wie folgt aus:
		Die Ebenen mit der gleichen Bezeichnung liegen senkrecht übereinander. Wir entfernen jetzt - z.B. durch Agglomeration von Leerstellen - eine Ebene teilweise, z.B. die mittlerer B- Ebene Die jetzt benachbarten A- und C- Ebenen relaxieren in die gezeigte Konfiguration. Entstanden ist ein Stapelfehler, da die Stapelsequenz ABCABCA.. nicht mehr stimmt; sie lautet jetzt ABCACABCA...Die Leerstellenscheibe ist offensichtlich von einer (Stufen)versetzung berandet. Was ist ihr Burgersvektor? Wenn wir statt Leerstellen Eigen-Zwischengitteratome kondensieren lassen; also partiell eine Ebene einführen, erhält man das folgende Bild: Die Stapelfolge ABCABCA... ist jetzt fehlerhaft mit der Sequenz ABCABACABCA... . Dies ist offenbar ein anderer Stapelfehler als der oben gezeigte. Aus historischen Gründen heißt der obige (Leerstellentyp) intrinsischer Stapelfehler, der hier gezeigte extrinsische Stapelfehler. Auch dieser Stapelfehler ist von einer Versetzung berandet. Um Burgersumläufe vornehmen zu können, müssen wir die Elementarzelle in die verwendete Projektion einzeichnen
	Aus der Voltaterra Definition (oder aus einem Umlauf) folgt sofort:
		Die Burgersvektoren der beiden Stapelfehler sind    b=± a/3 <111>    d.h. kein Translationsvektor des Gitters.
		Burgersvektoren von diesem Typ heißen auch Franksche Partialversetzungen
	Definition: Versetzungen mit Burgersvektoren die kein Translationsvektor des Gitters sind, heißen Partialversetzungen. Sie beranden notwendigerweise flächenhafte Defekte; hier Stapelfehler.
	Kleine "Stapelfehlerringe" sind die Primärdefekte, die durch Agglomeration von atomaren Fehlstellen entsthen.
	Stapelfehler können jedoch auch ohne Mitwirkung von atomaren Fehlstellen entstehen - Rezept nach Voltaterra:
		Mache fiktiven Schnitt zwischen z.B. der A- und B- Ebene
		Verschiebe die B- Ebene so, daß sie auf die C- Lage fällt. (Tennisballmodell).
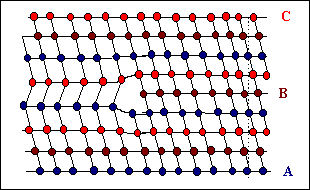
		Man erhält statt der Stapelfolge ABCABCA... jetzt ABCACABCA... , d.h. einen intrinsischen Stapelfehler
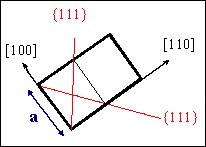
		Der Verschiebungsvektor=Burgersvektor der Partialversetzung ergibt sich, indem auf die {111} Ebenen die Elementarzelle projeziert wird
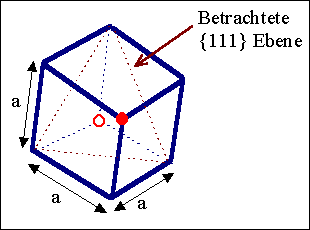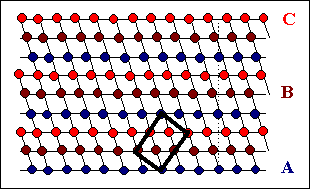
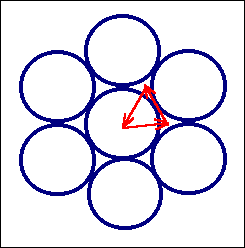
		Wenn die beiden roten Eckpunkte genau aufeinanderfallen, hat man die Projektion der linken Zeichnung.   Die rot eingezeichneten Vektoren verschieben jeweils eine {111} Ebene von einer A in eine B-Lage
		Die relevanten Verschiebungsvektoren sind vom Typ    b=a/6 <112> , sie heißen Shockleysche Partialversetzungen
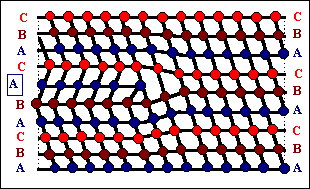
		Abbildung: Vergleich von Frank- und Shockley - Partialversetzungen in fcc-Kristallen in <110> Projektion.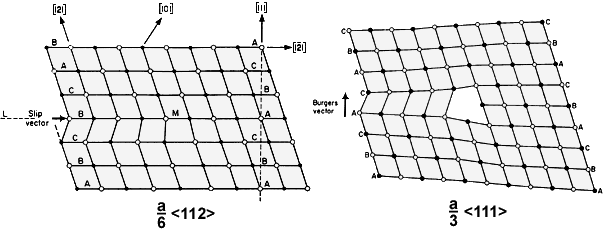
	Partialversetzungen sind nicht eine Erfindung gelangweilter Professoren, sondern: Es gibt in der Natur (zumindest in face-centered cubic Kristallen) in der Regel nur Partialversetzungen!