|
Die Herstellung und damit verbunden die plastische Verformung
von Metallen (also Kristallen) markiert den Beginn der Neuzeit; die
"Hütten- und Schmiedekunst" war lange der
"High-Tech" Bereich unserer Vorfahren. Nur durch "Versuch und
Irrtum" (trial and error) wurde im Lauf der Jahrtausende die
Metallherstellung und Verarbeitung immer mehr ausgeweitet und verfeinert - die
oft erstaunlich komplexen Produkte sind in Museen zu besichtigen. Im
Landesmuseum in Scheswig kann man z.B. sog. Damaszener-Schwerter der Wikinger
bestaunen. |
 |
Warum Metalle (im Gegensatz zu den meisten anderen Materialien)
sich plastisch verformen lassen, welche Vorgänge im atomaren Maßstab
dabei ablaufen, und warum die Verformungseigenschaften bei weitgehend gleicher
chemischer Zusammensetzung von vielen Faktoren sehr stark beeinflußt
werden können, wurde jedoch erst 1934 im Grundsatz geklärt - durch
die "Entdeckung" der Versetzung als fundamentalem
Kristallgitterdefekt durch Orowan, Taylor und Polyani (Vorher "Verhakungen" von
U. Dehlinger, Stuttgart 1929) |
|
 |
Abbildung:
Meilensteine der Versetzungsgeschichte.
|
 |
Versetzungen kann man sowohl anschaulich/
atomistisch, als auch kontinuumsmechanisch definieren und visualisieren (siehe
3-dim Darstellung einer
Versetzung, oder der Zugversuch im Seifenblasenmodell (Video1 (1,6 MByte),
Video2 (1
MByte)). |
|
 |
Die atomistische Beschreibung ist leicht verständlich, jedoch begrenzt
auf Versetzungen mit großen (unmittelbar "sichtbaren"
Auswirkungen) im Kristallgitter
Siehe hierzu auch: "Verformung eines Einkristalls" im
Video3 (1,3 MByte)
und Video4 (2
MByte), sowie elektronenmikroskopische Versetzungsbewegungen unter
mechanischer Spannung im Video5
(1,35 MByte)
Da die Autoren dieser wissenschaftlichen Filme
nicht mehr zu ermitteln sind, werden die evtl. Inhaber der Rechte gebeten, sich
an Prof. Dr. H. Föllzu
wenden! |
|
 |
Die kontinuumsmechanische Beschreibung ist allgemeiner, aber
abstrakter. |
 |
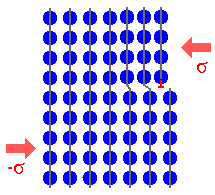
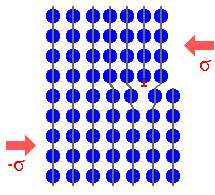
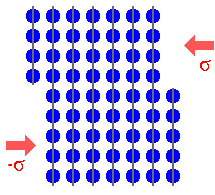
Atomistische Darstellung der plastischen
Verformung durch eine Stufenversetzung |
|
|
Hierzu gibt es auch eine
GIF-Animation. |
 |
Bereits dieses einfache Beispiel reicht aus, um
einige Eigenschaften von Versetzungen abzuleiten, die sehr allgemein gelten
müssen: |
|
 |
Die Versetzung ist ein eindimensionaler Defekt; nur
entlang der Versetzungslinie ist das Kristallgitter gestört, d.h.
(abgesehen von kleinen elastischen Dehnungen) von einem Idealgitter
verschieden. Die Versetzungslinie kann durch einen Linienvektor t
beschrieben werden. |
|
 |
Im Versetzungskern sind Bindungslängen und Bindungswinkel
nicht im Gleichgewicht - die Versetzung "besitzt" Energie (und
Entropie) pro Längeneinheit. |
|
 |
Versetzungen können sich bei Vorhandensein
äußerer Kräfte (bzw. dadurch erzeugter innerer Spannungen)
bewegen, die dadurch definierte Gleitebene enthält immer die
Versetzungslinie. |
|
 |
Durch die Versetzungsbewegung verschiebt sich der ganze
Kristall auf einer Seite der Gleitebene relativ zum ganzen Kristall auf der
anderen Seite. |
|
 |
Stufenversetzungen können im Prinzip durch
Agglomeration atomarer Fehlstellen entstehen.
|
 |
Die fundamentale Größe, die eine beliebige
Versetzung charakterisiert, ist ihr Burgers vektor b. Die atomistische
Definition ergibt sich aus dem Burgers-Umlauf im relevanten Kristallgitter.
Dabei wird ein beliebiger geschlossener Umlauf um eine Versetzungslinie als
Vektorkette der Basisvektoren des Gitters durchgeführt und mit einem exakt
korrespondierenden Umlauf im ungestörten Ideal- oder Referenzgitter
verglichen. |
|
|
 |
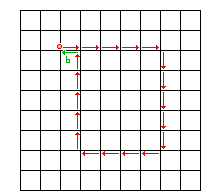 |
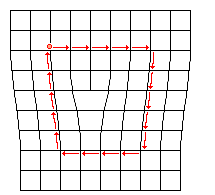
Ein Burgersumlauf um eine Stufenversetzung. |
|
|
 |
Der Schließungsfehler im Referenzkristall ist der
Burgersvektor der Versetzung. |
|
 |
Der Burgersvektor einer perfektenVersetzung ist damit
immer ein Gittervektor. |
 |
Achtung! Wie immer bei
Konventionen, ist die Vorzeichenwahl beliebig. In der hier vorgestellten
(gebräuchlichen) Version ist der geschlossene Umlauf um die Versetzung,
der Burgersvektor zeigt im Referenzkristall vom Ende des Umlaufs zum Start.
Möglich ist auch, einen geschlossenen Umlauf im Referenzkristall
durchzuführen, der b-Vektor ist dann im gestörten Kristall definiert,
er muß bei gleichem Vorzeichen dann aber vom Start- zum Endpunkt zeigen.
Für eine eindeutige Festlegung muß auch noch der Umlaufsinn
festgelegt werden (kommt später). Das richtige (d.h. konsistente)
Vorzeichen ist oft sehr wichtig! |
 |
Etwas unanschaulicher als die Stufenversetzung,
aber atomistisch noch darstellbar, ist die Schraubenversetzung. |
 |
Zur Veranschaulichung
dienen die folgenden Animationen eines Burgersumlauf um eine
Schraubenversetzung. |
|
 |
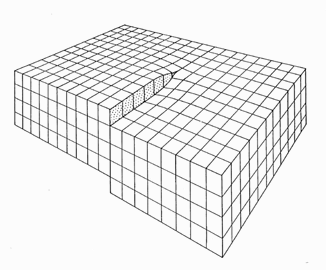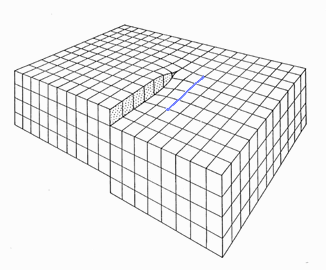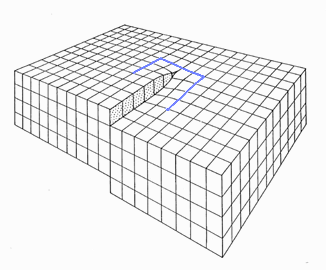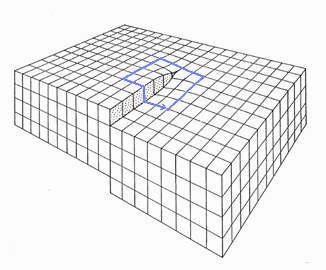
1. Weg, Umlauf um die Versetzung |
|
|
 |
|
|
Die atomistische Definition des Burgersvektors ergibt
sich aus dem Burgers-Umlauf im relevanten Kristallgitter. Dabei wird ein
beliebiger geschlossener Umlauf um eine Versetzungslinie als Vektorkette
der Basisvektoren des Gitters durchgeführt. Der Umlauf wird dann mit einem
exakt korrespondierenden Umlauf im ungestörten Ideal- oder Referenzgitter
verglichen. |
|
 |
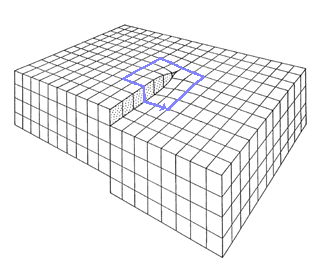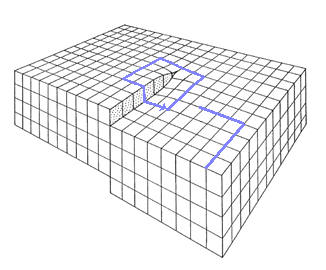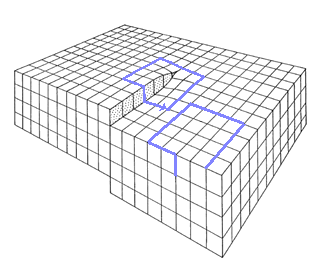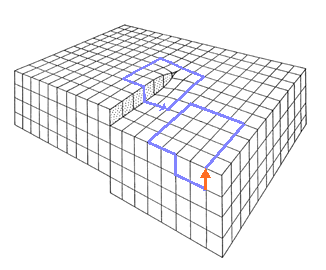
1. Weg, Vergleich mit dem ungestörten Kristall |
|
|
 |
|
 |
Bei dem Vergleich mit einem exakt korrespondierenden
Umlauf im ungestörten Ideal- oder Referenzgitter zeigt sich ein
Schließungsfehler.
|
|
 |
Dieser Schließungsfehler im Referenzkristall ist der
Burgersvektor der Versetzung. |
|
 |
Der Burgersvektor einer perfekten Versetzung ist
damitimmer ein Gittervektor. |
 |
Man kann den Burgersvektor auch
auf einem zweiten Weg erhalten... |