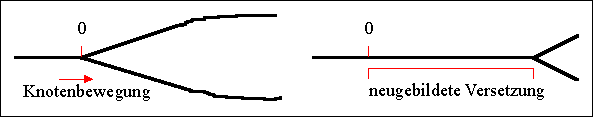 |
Da Versetzungslinien beliebig gekrümmt sein
können, und darüberhinaus auch Burgersvektoren vorkommen werden, die
viel "kleiner" sind als Translationsvektoren des Gitters (z.B.
b=a/6[112]), ist eine allgemeinere Definition der Versetzung sinnvoll und
notwendig. |
|
 |
Voltaterra hat schon 1907 eine kontinuumsmechanische
Definition gegeben, deren Übertragung auf ein (damals noch unbekanntes)
Kristallgitter sofort zum allg. Begriff der Versetzung führt. |
|
Abbildung:
Voltaterras 6
Grundverformungen - 3 davon entsprechen der Stufen bzw. Schraubenversetzung
|
|
Allgemeine Definition einer Versetzung nach
Voltaterra |
|
|
|
|
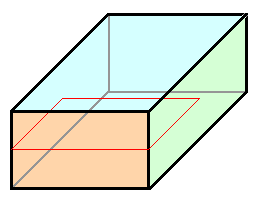
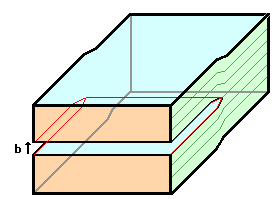
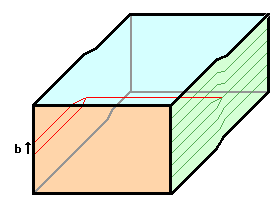
1. (Fiktiver) Schnitt in den Kristall; Die Schnittlinie
entspricht dem Linienvektor t der zu bildenden Versetzung |
|
|
 |
|
|
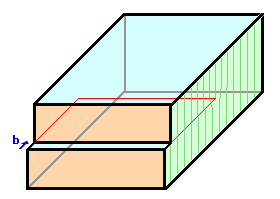
2. Verschieben der beiden Schnittebenen um einen
Translationsvektor des Gitters=± Burgersvektor b (Vorzeichen je
nach Konvention) |
|
|
  |
|
|
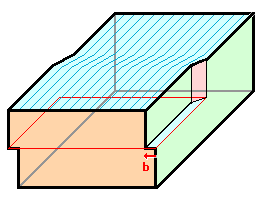
3. Falls nötig, Material entnehmen oder einfüllen
|
|
|
 |
|
|
4. Kristall wieder herstellen durch
"Verschweißen" der Schnittflächen |
|
Da der Verschiebungsvektor ein Translationsvektor des Gitters
war, passen die Schnittflächen überall außer entlang der
Schnittlinie perfekt zusammen. Es ist ein eindimensionaler Defekt
entstanden - die Versetzung mit Linienvektor=Schnittlinie;
Burgersvektor=Verschiebungsvektor.
Aus der Voltaterra-Definition werden weitere Eigenschaften von Versetzungen
unmittelbar klar. Die nachfolgende Liste ergänzt, ersetzt oder
präzisiert die bereits festgestellten Eigenschaften 1. - 4. |
|
|
5. Der Burgersvektor ist für eine gegeben
Versetzung überall gleich (dies gilt nicht für den
Linienvektor), da es nur eine Verschiebung der Schnittflächen
relativ zueinander gibt. |
|
|
6. Stufen- und Schraubenversetzung (mit einem
Winkel(t, b)=90° bzw. 0° zwischen dem Linienvektor
t und Burgersvektor b der Versetzung) sind Grenzfälle der
allgemeinen gemischten Vesetzung, mit Winkel(t, b)=beliebig. |
|
|
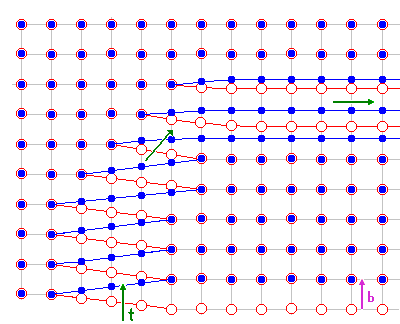
7. Abbildung: Atomistische Darstellung einer gemischten
Versetzung |
|
|
 |
|
|
Die rote Kreise symbolisieren Atome unterhalb der Gleitebene,
die blauen Kreise Atome oberhalb der Gleitebene. Im oberen Teil des Bildes
liegt eine Stufenversetzung vor (Linienvektor
t ist senkrecht zum Burgersvektor
b), im unteren Teil eine Schraubenversetzung (t ist
paralell zu b) . Dazwischen gibt es einen kontinuierlichen Übergang
vom Stufen- zum Schraubencharakter der Versetzung.
In der Animation ist die Versetzungsbewegung dieser Versetzung zu
sehen. Sie läuft aus dem Kristall heraus, d.h. die vorhandene Gleitstufe
wird verschwinden. |
|
|
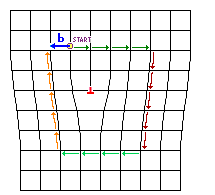
8. Der Burgersvektor muß unabhängig vom genauen
Verlauf des Burgersumlaufs sein. |
|
|
 |
 |
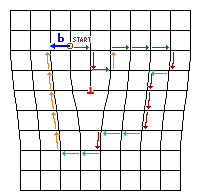Zwei beliebige Burgersumläufe um eine Stufenversetzung. Die farbliche
Markierung soll das "Abzählen" der Schritte Hoch und Runter
(Orange und Rot) sowie Rechts und Links (Dunkelgrün und Hellgrün)
unterstützen. |
|
|
|
9. Eine Versetzung kann nicht im Inneren eines perfekten Kristalls
enden, sonden nur
- an der Oberfläche,
- an einer inneren Grenzfläche (Korn- oder Phasengrenze), oder
- an einem Versetzungsknoten.
|
|
|
10. Verformung erfolgt durch Bewegung der Versetzung in der
Schnittebene=Gleiten in der Gleitebene, da ein
"Weiterschneiden" gleichbedeutend mit einer Bewegung der Versetzung
ist. |
|
|
11. Die Gleitebene wird damit aufgespanntdurch
Burgers- und Linienvektor. |
|
|
12. Der Betrag von b, (b) ist ein Maß für
die "Stärke", d.h. die elastischen Verzerrungen um eine
Versetzung.
|
|
Die letzte sehr wichtige Konsequenz aus der
Definition der Versetzung ist: |
|
|
13. An einem Versetzungsknoten ist die Summe der
Burgersvektoren=0, vorausgesetzt, alle t-Vektoren zeigen zum Knoten oder
vom Knoten weg. |
|
Die Begründung (der "Beweis")
für 13.kann auf zwei Arten gegeben werden: mit Burgers- Umlauf und mit der
Voltaterra-Definition - womit auch die Äquivalenz beider Beschreibungen
demonstriert wird. |
|
|
Sbi= 0 an einem Versetzungsknoten aus
Burgers-Umlauf: |
|
|
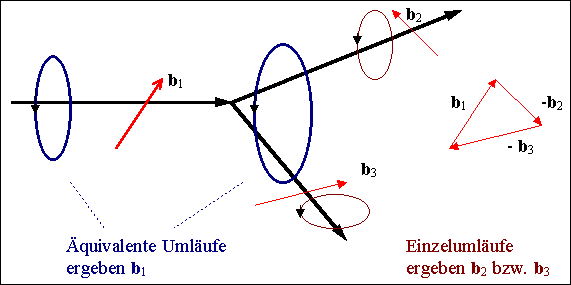Hieraus folgt die Konsequenz: b1=b2 +
b3, oder, bei Umnormierung auf: "Alle t-Vektoren
zeigen auf Knoten." Sbi= 0 im Knoten.
|
|
|
Gilt Sbi= 0 an einem Versetzungsknoten aus der
Voltaterra-Definition |
|
|
|
|
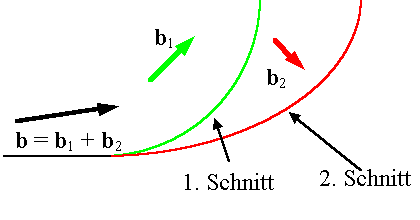
Einige Folgerungen aus den zuvor genannten
Punkten: |
|
|
|
|
Gleitebene eines Stufenversetzungsringes=Gleitzylinder |
|
|
 |
|
|
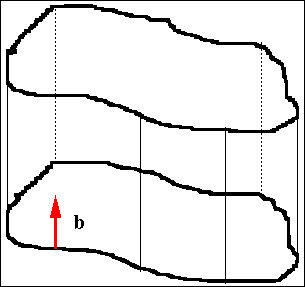Reine Schraubenversetzungen sind auf allen Ebenen
gleitfähig |
|
|
Für eindeutige Vorzeichenfestlegung fehlt noch eine
Konvention für das Vorzeichen des Linienvektors t sowie die
Festlegung des Umlaufsinns des Burgersumlaufs relativ zur Richtung des
Linienvektors. Einfache Regeln, die zu einer konsistenten Vorzeichengebung
führen sind: |
|
|
Wahl der Vorzeichen der Linienvektoren so, daß was in irgendeinen
Referenzknoten hineinfließt auch wieder herausfließt:
t1=t2 + t3.
Bei allen anderen Knoten ist dann diese Bedingung automatisch erfüllt,
aber Sb ist ungleich Null. |
|
|
 |
|
|
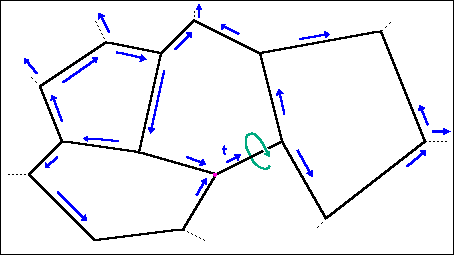Burgersumlauf nach Festlegung der Linienrichtung nach
"rechter Hand Regel". |
|
|
Burgersumlauf ist geschlossen um Versetzung;
Schließungsfehler im Referenzkristall "Finish to Start" ist
Burgersvektor b. |
|
|
|
Es bleiben aber einige Fragen offen; dies
läßt sich aus dem obigen Bild begründen: |
|
|
Gibt es auch 4er, 5er, ... -Knoten? |
|
|
Sind die Winkel in einem Knoten beliebig? |
|
|
Was bestimmt mögliche Versetzungsreaktionen, z.B. die
Bildung einer neuen Versetzung durch "Wandern" eines Knotens? |
|
|
|
|
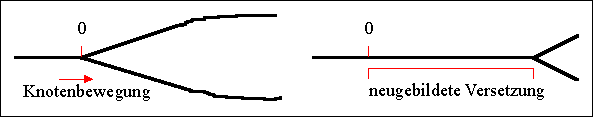
Zur Klärung müssen wir die
Energie einer Versetzung und die Wechselwirkung zwischen
Versetzungen wissen. |
|
Nochmal zu den Vorzeichen: Es ist sehr
tückisch, man muß aufpassen und besonders immer auf die
Linienrichtung achten.
Regel: Vorzeichenwechsel beit
heißt Vorzeichenwechsel bei b |
|
|
Beispiel: Versetzungsring |
|
|
|
|
|
Burgersvektoren an den herausgegriffenen Punkten
offensichtlich entgegengesetzt; aber b überall gleich nach
Voltaterra!??
Lösung: Vorzeichenwechsel bei t an den herausgegriffenen Punkten!
|
