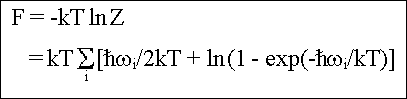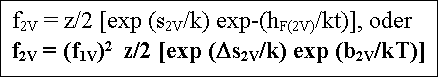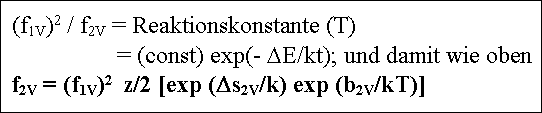| |
|
|
zu |
|
|
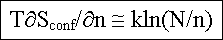 |
|
genähert.
Mit n/N=f=Konzentration der Leerstellen erhalten wir die altbekannte
Formel |
|
|
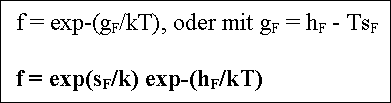
|
|
|
|
|
|
|
|
|
 |
Der Vorfaktor mit der Bildungsentropie ist dabei
neu gegenüber der alten Version. |
 |
Wie immer, können alle Voraussetzungen und
Näherungen hinterfragt werden.
Kurzbeispiele dazu: |
|
 |
Die Referenzenergie G0 des perfekten
Kristalls kann von der chemischen Umgebung abhängen. Sauerstoffleerstellen
eines Kristalls im Gleichgewicht mit einer Sauerstoffatmosphäre oder mit
Vakuum können dann stark betroffen sein (darauf basiert zum Teil die
Sensorik). |
|
 |
Die reine Gleichgewichtsbetrachtung sagt nichts
darüber aus, wie die Leerstelle erzeugt wurde, und wo das
überschüssige Atom jetzt ist. Die Anlagerung des
überflüssigen Atoms an reale Oberflächen oder andere Defekte
kann eigene Energieterme einbringen. |
|
 |
Es mag für eine Leerstelle (bei Zwischengitteratomen ist
dies unmittelbar einsichtig) mehr als eine Möglichkeit geben, sich auf
einen Atomplatz zu setzen (zusätzliche interne Freiheitsgrade; Entartung).
Dann muß ein weiterer (Entropie)Term zur freien Energie kommen, mit dem
Endergebnis:

Die Zdbzw. Z0 sind die Zustandsummen im Defekt- bzw. im
Referenzzustand. |
 |
Beispiele dazu: |
|
 |
Entartung wg. Spin (neutrale Leerstelle in
Ionenkristallen): Zd/Z0=2 |
|
 |
(Doppel)Leerstelle in body-centered cubic
Kristallen mit Vorzugsorientierung entlang [111]: Zd/Z0=4
|
|
|
| Berechnung und Bedeutung
der Bildungsentropie: |
 |
Herkunft aus geändertem Schwingungsspektrum
(Hinweis auf Entropie aus Schwingung zur Stabilität body-centered cubic;
Haasen S. 113) |
 |
Berechnung nach Seeger (Kurzdarstellung): |
|
 |
Harmonische Näherung; Kristall=Summe harm.
Oszillatoren |
|
 |
Energie eines Oszillators in
Quantenmechanik 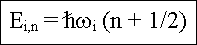 |
|
 |
Zustandssumme harm. Oszillator ist dann
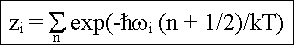 |
|
 |
Die Zustandssumme des Kristalls wird
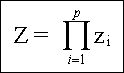 ,
wobei das Produkt über den ganzen Oszillatorsatz zu nehmen ist. (p=3N ;
N=Zahl Atome) ,
wobei das Produkt über den ganzen Oszillatorsatz zu nehmen ist. (p=3N ;
N=Zahl Atome) |
|
 |
Die freie Energie des Oszillatorsatzes ist
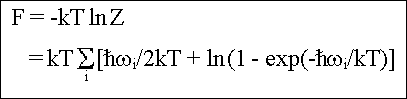 |
|
 |
Für die Entropie gilt
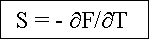 bei
konstantem Volumen bei
konstantem Volumen |
|
 |
Mit Einsetzen folgt
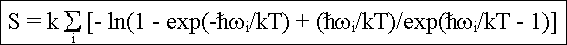
für die Entropie des Idealkristalls. |
|
|
Jetzt wird ein Kristall mit
einer Leerstelle betrachtet. Alle Eigenfrequenzen ändern sich von
wi nach w´i ; die Schwingungsentropie ist jetzt
S´. |
 |
Die Bildungsentropie
der einen Leerstelle ist damit
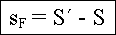
|
|
 |
Oberhalb der Debye Temperatur gilt immer
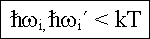 ;
damit ist eine Reihenentwicklung nach hquer omegai /kT
möglich und sinnvoll. ;
damit ist eine Reihenentwicklung nach hquer omegai /kT
möglich und sinnvoll. |
|
 |
Man erhält in erster Näherung
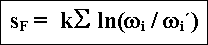 wobei über sämtliche Eigenfrequenzen des Kristalls summiert wird.
wobei über sämtliche Eigenfrequenzen des Kristalls summiert wird.
|
 |
Die Berechnung erfolgt in analytischer
Näherung nur für nächste Nachbarn der Leerstelle, mit
entsprechend geänderten Federkonstanten aus den Bindungspotentialen. Man
erhält: |
|
 |
sF(1 Leerstelle)=ca. 0.5
kBT (Cu) bis 1.3 kBT (Au) |
|
 |
sF (Doppelstelle)=ca. 1.8
kBT (Cu) bis 2.2 kBT (Au) |
|
Diese Werte passen zu den gemessen Werten (zur experimentellen
Bestimmung siehe Kapitel 4). Im
Umkehrschluß folgt daraus: |
 |
Die Bildungsentropie macht eine Aussage über die
räumliche Ausdehnung der atomaren Fehlstellen. Je größer
sF ist, desto mehr Atome um die atomare Fehlstelle herum sind
betroffen, d.h. haben ihre Eigenfrequenzen stark geändert. Es gelten
folgende Faustregeln: |
|
 |
sF » 1k entspricht
atomarem Defekt; 10k entspräche "Ausdehnung" auf 5 - 10
Atome |
|
 |
Atomare Fehlstellen in Elementkristallen liegen
bei sF » 1k; d.h. sind "atomar" oder
"Punktfehler". Die große Ausnahme ist |
|
 |
Silizium, mit sF » 6k -
15k, (aus Diffusionsmessungen); dies war der Anstoß zur Theorie
der "extended interstitials", denn für Eigenzwischengitteratome
gelten natürlich dieselben Beziehungen. |
Mehrfachleerstellen
(Zwischengitteratome - mit Modifikationen - analog)
|
 |
Bisher wurden alle atomaren Fehlstellen ohne
Wechselwirkung angenommen. Wechselwirkungen sind aber möglich, bei
Leerstellen sind sie in der Regel anziehend. Dies kann durch einfache
Überlegungen gefolgert werden: |
 |
Metalle |
|
 |
Das durch die Leerstelle entstehende
"Störpotential" im sonst periodischen Potential wird durch das
freie Elektronengas abgeschirmt (Rearrangement der Elektronen in der
Leerstelle). Die Bildungsenergie der Leerstelle ist im wesentlichen die Energie
zum Umverteilen des Elektronengases, die Relaxation der Nachbaratome trägt
nur wenig bei. |
|
 |
Entfernt man (gedanklich) neben einer bereits
vorhandene Leerstelle ein zweites Metallion, ist die jetzt aufzubringende
Arbeit kleiner, da ein Teil der notwendigen Abschirmungsarbeit bereits
geleistet wurde. |
|
 |
Anders ausgedrückt: Die Doppelleerstelle
besitzt eine gewisse Bindungsenergie (Größenordnung 0,1 - 0,2 eV).
|
 |
Valenzkristalle |
|
 |
Die Bildungsenergie einer Leerstelle wird im
wesentlichen durch das Aufbrechen von Bindungen bestimmt. Bei der Bildung einer
benachbarten Leerstelle müssen weniger Bindungen aufgebrochen werden;
wiederum kommt es zu einer Bindungsenergie. |
 |
Ionenkristalle |
|
 |
Die Leerstellen sind geladen. Dadurch kommt es zu
Coulomb-Wechselwirkungen, die im Falle benachbarter Leerstellen des Kationen
bzw. Anionenuntergitters anziehend sind. Im Unterschied zu den obigen
Fällen ist die Anziehung hier weitreichend. |
 |
Der wesentliche neue Parameter ist also die
Bindungsenergie b2V. Sie ist z.B. definiert
über die Reaktionsgleichung |
|
|
1V + 1V
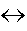 2V
+ b2V (Vorzeichen positiv bei Anziehung). 2V
+ b2V (Vorzeichen positiv bei Anziehung).
V ist das Formelzeichen für eine Leerstelle (Vacancy)) |
|
|
|
 |
Berechnung der Gleichgewichts-Konzentration von
Doppelleerstellen
|
 |
Weg 1: |
|
 |
Variation der gesamten freien Enthalpie (wie
gehabt) |
|
 |
Mit gF(2V)=hF(2V) - TsF(2V);
hF(2V)=2hF(1V) - b2V;
sF(2V)=2sF(1V) + D
s2V
(D s2V heißt Assoziationsentropie;
Größenordnung 1k - 2k in Metallen) erhält man
analog der Rechung für Einfachleerstellen |
|
|
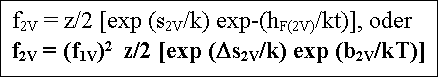 |
|
|
Der Faktor z/2 berücksichtigt dabei die verschiedenen
Anordungsmöglichkeiten einer Doppelleerstelle. z ist dabei einfach die
Koordinationszahl (Anzahl nächster (gleichartiger) Nachbarn) im Gitter
(flächenzentriert (fcc) ist z=12, im raumzentrierten (bcc) ist z=8 und im
Diamantgitter ist z=4) |
|
 |
Die Konzentration der Doppelleerstellen ist damit
immer sehr viel kleiner als die der Einfachleerstellen im thermischen
Gleichgewicht. |
|
 |
Typische Werte für Metalle am Schmelzpunkt:
f1V=10-4 - 10-3
f2V=10-6 - 10-5
|
 |
Weg 2: Berechung über Massenwirkungsgesetz
(MWG) |
|
 |
Zugrunde liegt die reversible Reaktion
1V + 1V
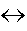 2V
2V |
|
 |
Damit folgt aus dem MWG sofort:
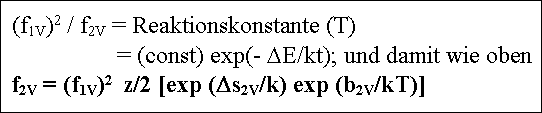
mit DE=freie Energie für Vorwärtsreaktion
(Die diversen Vorzeichenkonventionen ,damit alles stimmt, sind einerseits
sorgfältigst zu beachten wenn man wirklich rechnet, andererseits trivial,
und werden deshalb hier nicht näher ausgeführt). |
 |
Wichtig: Die MWG-Betrachung gilt allgemeiner,
nämlich nicht nur für das globale thermische Gleichgewicht, sondern
auch für Defektreaktionen außerhalb des Gleichgewichts, z.B. beim
Abkühlen des Kristalls, wenn die Leerstellen in zu hoher Konzentration
vorhanden sind (lokales Gleichgewicht; siehe Kap
2.2.3) |
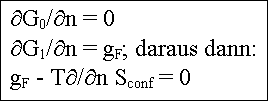
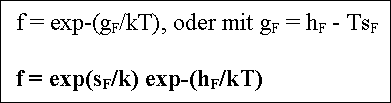
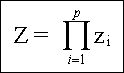 ,
wobei das Produkt über den ganzen Oszillatorsatz zu nehmen ist. (p=3N ;
N=Zahl Atome)
,
wobei das Produkt über den ganzen Oszillatorsatz zu nehmen ist. (p=3N ;
N=Zahl Atome)