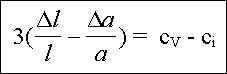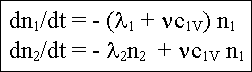4. Experimenteller Zugang zu (intrinsischen) atomaren Fehlstellen

4.1 Atomare Fehlstellen im Gleichgewicht

Dl/l - Da/a Methode

	Wie kann man direkt die Art und dieKonzentration messen, bzw. die Bildungsenthalpie und -entropie einer Defektsorte bestimmen?
		Einzige direkte Methode: Gleichzeitige Messung des Gitterparameters und der Dimensionsänderung der Probe, die
		(nach Simmons und Balluffi)
		Dabei ist die Grundidee, daß Dl/l - Da/a (l=Länge der Probe=l(T, Defekte) wegen thermischer Ausdehnung und Zusatzvolumen durch Defekte; a =Gitterkonstante=a(T) wegen thermischer Ausdehnung) für den idealen kristall ohne Defekte=0 ist, da beide Größen nur die thermische Ausdehnung beschreiben. Werden jetzt jedoch Leerstellen eingeführt und die fehlenden Atome auf die Oberfläche der Probe gebracht, ist Dl > Da; die Differenz entspricht gerade der Leerstellenkonzentration.
		Für einen kubischen Kristall mit vernachlässigbarer Relaxation der Atome um eine Leestelle (d.h. für jede Leerstelle erhöht sich das Kristallvolumen genau um ein Atomvolumen) gilt:
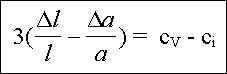
		d.h. die Differenz ist gleich der Differenz aus Leerstellen- und Zwischengitteratom-Konzentration.
		Experimentell werden hohe Anforderungen an die Meßgenauigkeit gestellt (Präzision im 10-5 Bereich), jedoch sind für die meisten Elementkristalle (=Metalle) solche Messungen erfolgreich durchgeführt worden. Außerdem müssen die Beiträge von Doppelleerstellen evtl. berücksichtigt werden.
	Beispiel einer Dl/l-Da/a Messung an Ag + 4% Sb (9 K)
	Einige gemessene Werte für die Einfachleerstelle für Elementkristalle (im wesentliche aus Dl/l - Da/a Messungen, aber auch aus anderen Methoden) zeigt die nachfolgende Tabelle (nach Seeger):
		Element cV bei Tm hF [eV] sF [k] Cu 2 x 10-4 1,04 0,3 Ag 1,7 x 10-4 0,99 0,5 Au 7,2 x 10-4 0,92 0,9 Al 9 x 10-4 0,65 0,8 Pb 1,7 x 10-4 0,5 0,7 Na 7 x 10-4     Li 4 x 10-4     Cd 6,2 x 10-4     Kr 3 x 10-3     Si keine Werte, Dl/l - Da/a=0 auch bei hoher Präzision
Postitronenvernichtung
	Eine weitere, allerdings aufwendige Methode, die Leerstellen im thermischen Gleichgewicht erfassen kann, ist die Postitronenvernichtung
	zu diesem Thema siehe auch: englisches Skript
		Dabei werden Positronen in die Probe geschossen, die dann mit Elektronen zerstrahlen unter Aussendung von (leicht) meßbarer) g - Strahlung. Die Zeit vom Eintritt in die Probe bis zur Zerstrahlung mit einem Elektron heißt (mittlere) Lebensdauer t; sie liegt im bereich 10-10 Sekunden. Die Lebensdauer ist eine Funktion der Elektronendichte.
		Leerstellen wirken nun auf Elektronen abstoßend und damit anziehend auf Positronen. Hält sich ein Positron bevorzugt in Leerstellen auf, wird seine Lebensdauer etwas verlängert, da es im Mittel eine kleinere Elektronendichte "sieht" als ein Positron das sich in Kristallgitter bewegt. Die gemessene Lebensdauer als Funktion der Temperatur enthält damit Information über die Leerstellenkonzentration.
	Einfache Theorie der Positronenvernichtung mit Leerstellen
		Es seien n0 Positronen (thermalisiert) im Gitter vorhanden, darunter n1 freie und n2 an Leerstellen gebundene, mit n0=n1 + n2. Die freien Positronen zerstrahlen entweder mit der Zerfallskonstanten l1=1/t1 oder werden mit einer Wahrscheinlichkeit n von Leerstellen eingefangen. Die an Leerstellen gebundenen Positronen zerstrahlen mit der Zerfallskonstanten l2 . Die zeitlichen Änderungen der Teilkonzentrationen ist dann
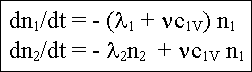	Dieses System von gekoppelten Differentialgleichungen mit der Anfangsbedingung n1(t=o)=n0 und n2(t=o)=0, läßt sich leicht lösen. Die gemittelte Lebensdauer t, die man im Experiment mißt, und die sich gewichtet aus den beiden Zerfallspfaden zusammensetzt, ergibt sich zu
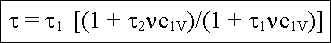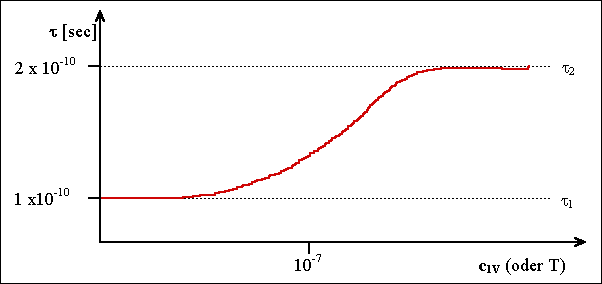
	Die Einfangwahrscheinlichkeit n läßt sich leicht abschätzen, man erhält für t den folgenden Verlauf in den richtigen Größenordnungen (allerdings kein Effekt bei Silizium):
	Der Vorteil bei der Positronenvernichtung liegt darin, daß ihre maximale Empfindlichkeit bei relativ niedrigen Temperaturen liegt (bei Konzentrationen der Leerstellen von 10-6 - 10-7); der Nachteil, daß für die quantitative Auswertung noch die Einfangwahrscheinlichkeit benötigt wird, außerdem sind die Experimente teuer; aber:
	Positronenvernichtung wird in der   gemacht (bei Herrn Faupel).
	Beispiele für Positronenlebensdauer in Ag(14K) und Positronenlebensdauer in Si und Ge (27K)
	Paper zur Positronenvernichtung: Untersuchung von Kristalldefekten mit Hilfe der Positronenannihilation (146kB)
Weitere direkte Methoden für Gleichgewicht:
Dieser Abschnitt ist im englischen Skript etwas ausführlicher!
	Weitere direkte Methoden für Gleichgewicht:
		Widerstand, spezifische Wärme als f(T) (experimentell schwierig)
		elektr. Rauschen (neu)
	Beispiel für Erholung mit Rauschen (32K)