|
How can we measure directly the type and concentration
of point defects and, if we do it as function of temperature, extract the formation energies
and formation entropies? |
|
 |
Simple question - but there is essentially only one direct
method: Measure the change of the lattice constant a, i.e. Da, and
the change in the specimen dimension, Dl, (one dimension is sufficient) simultaneously
as a function of temperature. |
|
 |
What you have then is the differential thermal expansion method also called the Dl/l
– Da/a method. |
|
 |
This method was invented by Simmons
and Balluffi around 1960. |
 |
The basic idea is that Dl/l –
Da/a (with l = length of the specimen = l(T, defects))
contains the regular thermal expansion and the dimensional change from point defects, especially vacancies.
|
|
 |
This is so because for every vacancy in the crystal an atom must be added at the surface;
the total volume of the vacancies must be compensated by an approximately equal additional volume and therefore an additional
Dl. |
|
 |
If we subtract the regular thermal expansion, which is simply given by the change in lattice
parameter, whatever is left can only be caused by point defects. The difference then
gives directly the vacancy concentration. |
|
 |
For a cubic crystal with negligible relaxation of the atoms into the vacancy (so the total volume of the vacancy provides added volume of the crystal), we have |
| |
| 3 | æ
ç
è
| Dl
l |
– |
Da
a |
ö
÷
ø | = |
cV – ci |
|
|
|
 |
With cV = vacancy concentration, ci = interstitial
concentration. |
|
 |
We have to take the difference of the concentration because
interstitial atoms (coming from a vacancy) do not add volume. |
 |
This is quite ingenious and straightforward, but not so easy to measure in practice. |
|
 |
The measurements of both parameters have to be very precise (in the 10– 5
range); you also may have to consider the double vacancies. |
|
 |
But successful measurements have been made for most simple crystals including all important
metals, and it is this method that supplied the formation energies and entropies for most important materials. |
 |
The link shows a successful measurement
of Dl/l – Da/a for Ag
+ 4% Sb. |
 |
Some values mostly obtained with that method are shown in the following table
(after Seeger): |
| |
| Element |
cV at Tm |
HF [eV] |
SF [k] |
| Cu | 2 x 10–4 |
1,04 | 0,3 |
| Ag | 1,7 x 10–4 |
0,99 | 0,5 |
| Au | 7,2 x 10–4 |
0,92 | 0,9 |
| Al | 9 x 10–4 |
0,65 | 0,8 |
| Pb | 1,7 x 10-4 |
0,5 | 0,7 |
| Na | 7 x 10–4 |
|
|
| Li | 4 x 10–4 |
|
|
| Cd | 6,2 x 10–4 |
|
|
| Kr | 3 x 10–3 |
|
|
| Si |
no values, Dl/l – Da/a
= 0 even at ultra-high precision |
|
 |
A somewhat exotic, but still rather direct method is measuring the time constant
for positron annihilation
as a function of temperature to obtain information about vacancies in thermal equilibrium. |
|
 |
What you do is to shoot positrons into your
sample and measure how long it takes for them to disappear by annihilation with an electron in a burst of g
- rays. The time from entering the sample to the end of the positron is its (mean) life time t.
|
|
 |
It is rather short (about 10–10 seconds), but long enough to be measured, and it varies with the concentration of vacancies in the sample. Since electrons are needed for
annihilation and a certain overlap of the wave functions has to occur, the life time t
is directly related to the average electron concentration available for annihilation. |
|
 |
A nice feature of these technique is that the positron is usually generated by some radioactive decay event,
and then announces its birth by some specific radiation emitted simultaneously. Its death is also marked by specific g rays, so all you have to do is to measure the time between two special bursts of radiation. |
 |
Vacancies are areas with low electron densities. Moreover, they are kind of attractive to a
positron because they form a potential well for a positron - once it falls in there, it will be trapped for some time. |
|
 |
Since an average life time of 10–10 s is large enough for the positron, even after
it has been thermalized, to cover rather large distances on an atomic scale, some positrons will be trapped inside vacancies
and their percentage will depend on the vacancy concentration. |
|
 |
Inside a vacancy the electron density is smaller than in the lattice, the trapped positrons will enjoy
a somewhat longer life span. The average life time of all positrons will thus go up with an increasing number of vacancies,
i.e. with increasing temperature. |
 |
This can be easily quantified in a good approximation as follows. |
|  |
Lets assume that on the average we have n0 (thermalized) positrons in the lattice,
split into n1 "free" positrons, and n2 positrons trapped in
vacancies; i.e. |
| |
|
|
 |
The free positrons will either decay with a fixed rate l given by l1 = 1/t1, (with t1
= (average) lifetime), or are trapped with a probability n by vacancies being present
in a concentration cV. |
|
 |
The trapped positrons then decays with a rate l2
which will be somewhat smaller then l1 because it lives a little longer; its
average lifetime is now t2. |
|
 |
The change in the partial concentration then becomes |
|
|
dn1
dt |
= |
– (l1 + n
· cV) · n1 | | |
| |
dn2
dt |
= |
– l2 · n2 + n
· cV · n1 |
|
|
 |
This system of coupled differential equation is easily solved (we will do that as an exercise), the starting conditions are |
|
|
| n1(t = 0) | = |
n0 | | |
| |
| n2(t = 0) | = |
0 |
|
|
|
 |
The average lifetime t, which is the weighted average of the decay paths
and what the experiment provides, will be |
| |
| t |
= t1 · |
æ
ç
è |
1 + t2 · n ·
cV
1 + t1 · n ·
cV | ö
÷
ø |
|
|
 |
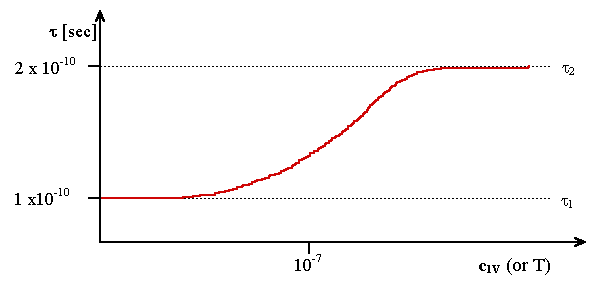
The probability n for a positron to get trapped by a vacancy
can be estimated with relative ease, the following principal "S"
- curve is expected. By now, it comes as no surprise that no effect was found for Si. |
| |
|
 |
The advantage of positron annihilation experiments is its relatively high sensitivity for low
vacancy concentrations (10–6 - 10–7 is a good value), the obvious disadvantage
that a quantitative evaluation of the data needs the trapping probability, or cross section for positron capture. |
 |
Some examples of real measurements and further information are given in the links:
Life time of positrons in Ag
Life time of positrons in Si and Ge.
Paper (in German): Untersuchung von Kristalldefekten mit Hilfe der Positronenannihilation
|
|
 |
A large table containing values for HF
as determined by positron annihilition (and compared to values obtained otherwise) can be found in the link |
| | |
| |
|
| | |
|
More Direct Methods for Measuring Point Defect
Properties |
| |
|
 |
There isn't much. Some occasionally used methods are |
|
 |
Measurements of the resistivity. Very suitable to ionic
crystals if the mechanism of conduction is ionic transport via point defects. But you never know for sure if you are measuring
intrinsic equilibrium because "doping" by impurities
may have occurred. |
|
 |
Specific heat as a function of T. While there should
be some dependence on the concentration of point defects, it is experimentally very difficult to handle with the required
accuracy. |
|
 |
Measuring electronic noise. This is a relatively new method which relies
on very sophisticated noise measurements. It is more suited for measuring diffusion properties, but might be used for equilibrium
conditions, too. The illustration in the link shows a noise measurement
obtained upon annealing frozen-in point defects. |
 |
However, the view presented above (and in the chapters before) is not totally unchallenged.
There are serious scientists out there who claim that things are quite different, especially with respect to equilibrium
concentrations of vacancies in refractory metals, because the formation entropy is much higher than assumed. |
|
 |
The method of choice to look at this is calorimetry at high temperature,
i.e. the measurement of the specific heat. A champion of this viewpoint is Y. Kraftmakher, who just published a book to this point. |
© H. Föll (Defects - Script)