HTML-Faksimile des Fachartikels:
Im Jahre 1928 sagte DIRAC auf Grund der relativistischen Gleichung des Elektrons (Dirac-Gleichung) die Existenz von Positronen voraus, die die Eigenschaften des Elektrons, aber eine positive Ladung besitzen sollten [1]. 1932 wurden von ANDERSON in der kosmischen Strahlung Teilchen entdeckt, die später als Positronen identifiziert wurden [2, 3].
Die Wechselwirkung von Positronen mit Festkörpern wurde mit der sich verbessernden Meßtechnik Ende der sechziger Jahre intensiver untersucht. Dabei wurde erkannt, daß sich mit Positronen Impulsdichten der Elektronen darstellen lassen. Informationen aus dem k-Raum werden deshaIb direkt gewonnen, weil die Erhaltungssätze von Energie und Impuls des Elektron-Positron-Paares vor und nach der Annihilation gelten und daher Informationen über den Elektronenimpuls in der Annihilationstrahlung enthalten sein müssen. Dies kann ausgenutzt werden, um die Impulsdichte der Elektronen im Festkörper zu messen und die Fermi-Fläche zu rekonstruieren.
Weiterhin können Positronen, die durch das Kristallgitter diffundieren, durch das lokal negative Potential eines Defektes bis zur Annihilation gebunden werden. Bei der Annihilation ändern sich dann die Eigenschaften der Annihilationsstrahlung charakteristisch. Damit konnte das Positron als Sonde zur Untersuchung von Defekten eingesetzt werden. Als Positronenfallen kommen u. a. Leerstellen, Leerstellenagglomerate, Versetzungen und Ausscheidungen in Frage.
Die Methode etablierte sich unter der Bezeichnung Positronenannihilation und wurde in den siebziger Jahren methodisch so weit entwickelt, daß bestimmte Anwendungsgebiete, wie die Untersuchung von Leerstellen in Metallen und Legierungen, als Standardanwendung gelten können. Eine Übersicht über diese Phase der Entwicklung wurde durch HAUTOJÄRVI in [4] gegeben. Seit dieser Zeit finden auch dreijährig internationale Positronenkonferenzen statt, die die neuesten Entwicklungen dokumentieren (zuletzt: 9. ICPA, August 1991 in Szombathely/Ungarn). Hier ist abzulesen, daß heute die Methode im wesentlichen für die Defektuntersuchung in Festkörpern ein wird. Neue Tendenzen sind in den letzten Jahren vor allem in der Hinwendung auf weitere Anwendungsgebiete, wie Halbleiter und Hochtemperatursupraleiter, zu sehen.
Die entscheidende methodische Weiterentwicklung der letzten Jahre ist die Entwicklung der Positronenstrahltechnik (auch Technik der "langsamen Positronen") zur Untersuchung von Defektprofilen in der Nähe von Ober- und Grenzflächen. Diese Entwicklung trägt der Forderung moderner Technologien Rechnung, bei denen Defekte in dünnen Schichten untersucht werden sollen (Oberflächenvergütung, Halbleiterepitaxie) [5]. Die Grundlagen dieser Untersuchungs-methode werden im zweiten Teil dieser Publikation vorgestellt [6].
Als Quellen werden im Labor in der Regel Isotope verwendet, die mit einem ß+-Zerfall Positronen durch geeignet gewählte geometrische Anordnung direkt in die Probe emittieren. Am häufigsten wird hierbei 22Na verwendet, da dieses Isotop eine relativ große Halbwertszeit (2,6 Jahre), eine hohe ß+-Ausbeute (90,69%) und einen geringen Preis (ca. 10-11 DM/e+) besitzt. Außerdem wird mit jedem Positron ein g-Quant von 1,28 MeV Energie emittiert, so daß Positronenlebensdauermessungen durch die Bestimmung der Zeitdifferenz zwischen dem Auftreten dieses Quants und den Annihilationsquanten (0,511 MeV) möglich werden. Die entstehenden Positronen haben durch die Natur des ß+- Zerfalls eine breite Energieverteilung zwischen 0 und 0,54 MeV.
Es werden Quellen unterschiedlicher Aktivitäten benötigt: etwa 5 x 105 Bq für Messungen der Positronenlebensdauer und des Doppler-Effektes (vgl. Kap. 4.1 und 4.3) und Aktivitäten von etwa 0,5 - 5 109 Bq für die Winkelkorrelation und die Strahltechniken (Kap. 4.2 und Teil 2 [6]). Die schwächeren Quellen werden durch Verdampfen von 22NaCl auf dünnen Metall- oder Plastikfolien erhalten und dann mit demselben Material abgedeckt. Die Quelle wird zur Messung mit zwei identischen Probenhälften umgeben ("Sandwich-Anordnung"). Die stärkeren Quellen entstehen durch Verdampfen des Isotops in einer Metallkapsel, die durch ein dünnes Metallfenster geschlossen wird. Die Positronen werden dann in der Apparatur mit magnetischen oder elektrischen Feldern im Vakuum bis zur Probe geführt.
Wenn Positronen in Festkörper eindringen, verlieren sie durch unelastische Streuung und bei geringeren Energien durch Phononenanregung bald ihre hohe Anfangsenergie und sind schon nach wenigen Pikosekunden im thermischen Gleichgewicht mit dem Festkörper (Thermalisation). Das Eindringen der Positronen in den Festkörper folgt einem exponentiellen Gesetz. Die mittlere Eindringtiefe hängt vor allem von der Kernladungszahl des Festkörpers ab und beträgt einige 10 bis 100 µm.

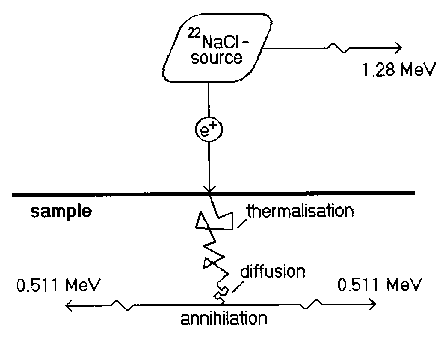
Abb. 1 Schematische Darstellung des Positronenexperimentes. Die in den Festkörper eindringenden Positronen werden in kurzer Zeit thermalisiert und diffundieren dann bis zu ihrer Annihilation durch das Material.
Nach der Thermalisation beginnt das Positron im Festkörper zu diffundieren und wird dann nach seiner mittleren Lebensdauer mit einem Kristallelektron annihilieren. Die Annihilationsstrahlung besteht in der Regel aus zwei nahezu kollinearen g-Quanten mit einer Energie von jeweils 511 keV (Masse-Energie-Umwandlung). Die mittlere Lebensdauer wird durch die Elektronendichte des Festkörper bestimmt Die Zerfallsrate l (reziproke Lebensdauer) ergibt sich aus
![]() (1)
(1)
Dabei stellt g einen Steigerungsfaktor dar, der die Erhöhung der Elektronendichte am Ort des Positrons durch die Positron-Elektron-Wechselwirkung beschreibt. l0 ist die Sommerfeldsche Annihilationsrate, die sich aus dem klassischen Elektronenradius r0, der Lichtgeschwindigkeit c und der Elektronendichte ne, ergibt. Typische Lebensdauerwerte in Festkörpern liegen zwischen 100 und 300 ps (Kap. 4.1).
Die Gesamtenergie der bei der Annihilation entstehenden g-Quanten entspricht der Energie des Elektron-Positron- Paares einschließlich der Ruhemasse und beträgt bei der hauptsächlich auftretenden 2 g-Annihilation jeweils etwa 511 keV. Der Impuls des Elektron-Positron-Paares ist wegen des geringen Impulses des Positrons nach der Thermalisation im wesentlichen gleich dem Elektronenimpuls. Eine Impulskomponente senkrecht zur Ausbreitungsrichtung der g- Quanten führt zur Abweichung von der Kollinearität der Annihilationsstrahlung um einen geringen Winkelbetrag
![]()
Die Impulskomponente in Ausbreitungsrichtung führt dagegen zur Doppler-Verbreiterung der Annihilationslinie. Diese beiden Effekte werden durch die Techniken der Winkelkorrelation (Kap. 4.2) und der Doppler-Messung (Kap. 4.3) nachgewiesen und können zur direkten Bestimmung der Impulsdichteverteilung der Elektronen im k-Raum benutzt werden.
Abb. 2 schematische Darstellung des auf Positronen wirkenden Potentials in der Nähe einer Leerstelle. E+ ist die Nullpunktsenergie des Positrons im Bloch-Zustand, EB die Bindungsenergie des Positrons an eine Leerstelle. Unten: einfaches Potentialtopfmodell für geladene (V+ und V-) bzw. neutrale Leerstellen (V0)
Im defektfreien Kristallgitter bewegt sich das Positron nach der Thermalisation als Bloch-Teilchen vorwiegend in den Zwischengitterbereichen, und die Annihilation erfolgt bevorzugt mit den Valenzelektronen. Wenn sich das Positron auf seinem Diffusionsweg durch das Material befindet (mittlere Diffusionsweglänge 100 nm), kann es durch Haftstellen mit einem negativen Potential bis zu seiner Annihilation gebunden werden. Dafür kommen Kristalldefekte mit offenem Volumen in Frage, wie z. B. Leerstellen, Leerstellenagglomerate und Versetzungen.
Bei der Diffusion im Kristallpotential werden die Positronen von den positiven Atomrümpfen abgestoßen. Liegt eine neutrale Leerstelle auf dem Diffusionsweg, kann das verminderte Potential zur Lokalisation des Positrons bis zur Annihilation führen. Diese Verminderung ergibt sich aus Veränderungen der Positron-Ion-Wechselwirkung, des Coulombpotentials und der Positron-Elektron-Korrelationsenergie und kann bis zu einigen eV betragen.
Eine Ladung der Leerstelle wird in Metallen durch das freie Elektronengas abgeschirmt, führt jedoch in Halbleitern und Isolatoren zu einem zusätzlich überlagerten langreichweitigen Coulomb-Potential. Für eine negative Ladung V- wird der Positroneneinfang wahrscheinlicher. Für eine zusätzliche positive Ladung ergibt sich eine Potentialschwelle, die thermalisierte Positronen normalerweise nicht überschreiten können. Die Positronen werden nicht an einer Haftstelle lokalisiert und annihilieren in ungestörten Kristallbereichen.
Neben Leerstellen können Positronen auch in anderen Defekten lokalisiert werden. Dazu gehören u. a. Versetzungen, Leerstellenagglomerate und Ausscheidungen, wie im Kap. 6 an verschiedenen Beispielen gezeigt wird. Kein Einfang wird an Zwischengitteratomen, Fremdatomen und Stapelfehlern beobachtet.
Bei der Annihilation aus dem gebundenen Zustand eines Defektes verändern sich die Annihilationsparameter (vgl. Kap. 5). Die Lebensdauer erhöht sich infolge der verringerten Elektronendichte in der Leerstelle. außerdem annihilieren die Positronen hier vermehrt mit Elektronen geringerer Impulse, wodurch die Verteilung der 2 g-Winkelkorrelation der Annihilationsquanten und das Verhalten der Doppler-Verbreiterung der Annihilationslinie signifikant geändert wird. Dies kann ausgenutzt werden, um Defekte nachzuweisen. Die Empfindlichkeit der Methode ist durch die Diffusionslänge der Positronen gegeben. Ist die Defektdichte hoch, wird jedes Positron auf seinem Diffusionsweg eingefangen und es ergeben sich die defekttypischen Annihilationsparameter. Bei Defektabständen, die sehr viel größer als die Diffusionsweglänge sind, werden kaum noch Positronen lokalisiert, es werden die Volumenwerte für die Annihilationsparameter erhalten.
Für die Messung der Lebensdauer eines Positrons, das von einer 22Na-Quelle emittiert wird, wird die Zeit zwischen dem Auftreten des Geburtsquants und den Annihilationsquanten durch eine elektronische Start-Stopp-Messung mit Hilfe eines Zeit-Impulshöhen-Konverters (ZIK) bestimmt (Abb. 3).
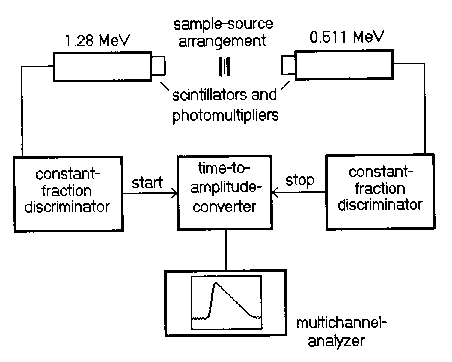
Abb. 3 Das Blockschaltbild des Lebensdauermeßplatzes
Die Quanten erzeugen in Szintillatoren mit gutem dynamischen Verhalten (BaF2- oder Plastikszintillatoren) Photonen im infraroten oder sichtbaren Bereich, die durch Kurzzeit-Sekundärelektronenvervielfacher in elektrische Impulse umgewandelt werden. Diese Impulse werden durch Fensterdiskriminatoren verarbeitet, die durch das "Constant-Fraction-Prinzip" einen hohen dynamischen Bereich für die Eingangsimpulse garantieren. Die Einstellung der Spannungen für die Energiefenster der differentiellen Diskriminatoren entspricht 1,28 MeV auf der Start-Seite und 0,511 MeV auf der Stopp-Seite des ZIK. Der ZIK wandelt durch Konstantstromladung eines Kondensators, die durch die Eingangsimpulse gestartet und gestoppt wird, die Zeitdifferenz in einen Ausgangsimpuls mit entsprechender Amplitude um, der durch einen Vielkanalanalysator registriert wird. Um Fehlmessungen durch die Vermischung von Quanten unterschiedlicher Annihilationsereignisse zu vermeiden, muß durch entsprechend geringe Quellaktivitäten (ca. 0,5 MBq) garantiert werden, daß sich in der Regel nur ein Positron in der Probe befindet. In 1 bis 3 Stunden wird auf diese Weise ein Lebensdauerspektrum mit ca. 2 Mill. Ereignissen akkumuliert.
Das Spektrum besteht aus einer Summe von Exponentialfunktionen (vgl. Kap. 5.1), deren Parameter (Zerfallskonstanten bzw. Lebensdauerwerte und deren Intensitäten) durch nichtlineare Regression aus den Spektren gewonnen werden. Die apparative Auflösungsfunktion (Zeitauflösung) ist eine Gaußkurve, die durch Überfalten der anzupassenden Modellfunktion berücksichtigt wird. Der Datenanalyse sind durch die relativ schlechte Zeitauflösung (ca. 180-250 ps) Grenzen gesetzt. So lassen sich zwei, höchstens drei Lebensdauerkomponenten separieren, deren physikalische Bedeutung in Kap. 5 näher erläutert wird.
Wenn die Impulskomponente des Elektron-Positron-Paares senkrecht zur Ausbreitungsrichtung der Quanten im Moment der Annihilation von Null verschieden ist, bilden die Quanten aus Gründen der Impulserhaltung einen von 180º leicht abweichenden Winkel (Abb. 4).
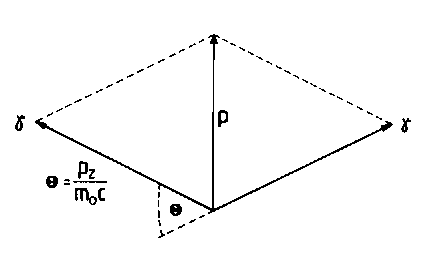
Abb. 4 Infolge der Impulserhaltung spannen die beiden Annihilationsquanten einen Winkel auf, der aus dem Impuls des Elektron-Positron-Paares vor der Annihilation resultiert.
Diese Winkelabweichung, die kleiner als 2º ist, läßt sich durch ein Koinzidenzverfahren bestimmen. Zu diesem Zweck werden zwei Matrizen von Detektoren mit der Probe in einer Linie angeordnet (Probe in der Mitte). Eine Koinzidenzschaltung ermittelt die zu einem Annihilationsereignis gehörenden Quanten und deren Abweichung von der Kollinearität, die in zwei Dimensionen durch einen Prozeßrechner berechnet und registriert wird.
Auf diese Weise wird die zweidimensionale Verteilung der Elektronen im Impulsraum gemessen. Über die dritte Richtung im k-Raum (Ausbreitungsrichtung der Quanten) wird integriert, da die Impulskomponente hier zur Doppler-Verschiebung der Annihilationslinie führt und diese geringe Energieveränderung von den ortsempfindlichen Detektoren nicht aufgelöst werden kann. Durch Verwendung von Einkristallen und durch die Auswertung mehrerer Orientierungen der Probe kann aber doch die Fermi-Fläche rekonstruiert werden. Dies ist allerdings nur dann möglich, wenn die Positronen vollständig aus der Matrix annihilieren und nicht durch Defekte eingefangen werden. Sollten sie dagegen vollständig durch Defekte eines Typs lokalisiert werden, so kann die Elektronenstruktur dieses Defektes untersucht werden.
Wie oben erwähnt, führt eine Impulskomponente des Elektron-Positron-Paares in Ausbreitungsrichtung der Quanten px zur Doppler-Verschiebung der Annihilationslinie, wobei die Energieverschiebung dE = px c /2 beträgt. Werden viele Ereignisse registriert, so tritt diese Impulskomponente mit positivem und negativem Vorzeichen auf. Damit kommt es zur Doppler-Verbreiterung der Linie, die mit einem hochauflösenden energiedispersiven Spektrometer registriert werden kann. Die Probe-Quelle-Anordnung ist hier wie bei der Lebensdauertechnik ein "Sandwich" aus zwei identischen Probenhälften und der durch sie eingeschlossenen schwachen Positronenquelle. Innerhalb einer Stunde wird ein Spektrum mit etwa 2 Mill. Ereignissen registriert. Die Energieauflösung der verfügbaren Detektoren liegt in der Größenordnung von ca. 1 keV und ist damit wesentlich schlechter als die vergleichbare Winkelauflösung der Winkelkorrelationstechnik. Damit kommen Untersuchungen der Elektronenstruktur mit Hilfe der Doppler-Technik nicht in Frage. Jedoch läßt sich diese Methode sinnvoll für Realstrukturuntersuchungen einsetzen, da die g-Linienformmessung mit hoher Statistik, schwachen Quellen und geringerem Aufwand zu ähnlichen Resultaten führt, wie man sie mit der Winkelkorrelationstechnik gewinnt.
Wie im Kap. 3 beschrieben, können Positronen während ihrer Diffusion durch das Potential von Kristalldefekten bis zu ihrer Annihilation lokalisiert werden. Sie ändern dort ihre Annihilationsparameter, die mittlere Positronenlebensdauer wird größer, die Winkelkorrelations- und Doppler-Kurven schmaler. Dies kann zur Bestimmung der Defektkonzentration und zur Untersuchung der Defektkinetik benutzt werden. Quantitativ wird der Positroneneinfang durch das sogenannte "Trapping-Modell" beschrieben, wobei hier nicht der quantenmechani-sche Prozeß des Einganges an sich, sondern die zeitliche Verteilung der Positronen auf die verschiedenen Defektzustände im Mittelpunkt steht.
Eine generalisierte Form des Trappingmodells wurde von SEEGER im Jahre 1974 angegeben [7]. Hier werden beliebig viele Defektarten zugelassen und auch die Möglichkeit des thermisch angeregten Entweichens aus dem Defekt berücksichtigt. Dieses Modell soll hier am einfachen Fall eines Defektes ohne Entweichen (z. B. Leerstellen in Metallen bei Raumtemperatur) erläutert werden.
Das Positron, das sich zur Zeit t = 0 (die Thermalisation kann im Vergleich zur Lebensdauer vernachlässigt werden) im Kristallvolumen (bulk, Index b) aufhält, kann von dort mit der Zerfallsrate lb annihilieren, wenn es nicht durch eine Leerstelle eingefangen wird. Im letzten Fall wird es mit der Einfangrate c lokalisiert und wird dann aus den Leerstellen mit der Annihilationsrate lv, (v für Leerstelle) annihilieren. Die Einfangrate ist eine Funktion der Leerstellenkonzentration und wird um so größer, je geringer der mittlere Abstand zwischen zwei Leerstellen ist. Die Annihilationsraten entsprechen den reziproken Lebensdauern, li = 1 / ti. Die zeitliche Änderung läßt sich mit einem System gekoppelter Differentialgleichungen beschreiben:
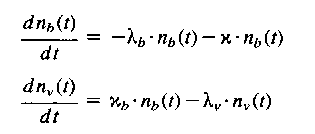 (2)
(2)
Es gelten die Anfangsbedingungen nb(0) = 1 und nv(0) =0. Die Lösung dieses Gleichungssystems liefert die relative Gesamtzahl der Positronen in der Probe zur Zeit t:
![]() (3)
(3)
Es ergibt sich eine Summe von Exponentialfunktionen. l1, l2 und l2 stehen in Gleichung (3) als Abkürzungen für:
![]() (4)
(4)
Die Zerfallsraten wurden hier wieder in der Form von Lebensdauern angegeben. Diese Lebensdauern und Intensitäten können aus den experimentellen Spektren durch die im Kap. 4.1 beschriebene Anpassung ermittelt werden. Man erkennt, daß die Lebensdauer t2 nicht von c, also nicht von der Defektkonzentration abhängt. Sie ist damit charakteristisch für den jeweiligen Defekttyp. Die mittlere Positronenlebensdauer tm ergibt sich aus
![]() (5)
(5)
h ist dabei der in Defekten annihilierende Teil der Positronen:
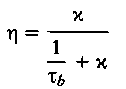 (6)
(6)
Die Einfangrate kann aus den Gleichungen (4) berechnet werden. Die Gleichungen sind überbestimmt und man kann die Formel für t1 dazu benutzen, den experimentell ermittelten Wert mit dem modellmäßig berechneten zu vergleichen. Ergeben sich Abweichungen, ist das Modell (eine Defektart nicht wechselwirkender Defekte; kein Entweichen aus den Defekten) falsch gewählt und die Analyse ist mit einem realistischeren Modell zu wiederholen. Wenn man auf diesen Vorteil verzichtet, kann man die Einfangrate auch aus der mittleren Lebensdauer tm bestimmen:
![]() (7)
(7)
Das hat den Vorteil, daß auf die Zweikomponentenzerlegung mit ihren numerischen Unsicherheiten verzichtet werden kann. Die Lebensdauern tb und tv müssen dann aus früheren Experimenten bekannt sein.
Auch aus den Spektren der Winkelkorrelation bzw. der Doppler-Verbreiterung läßt sich die Positroneneinfangrate bestimmen. Wie oben bereits erläutert, wird die Kurve schmaler, wenn Positronen durch Defekte eingefangen werden. Dies resultiert aus dem höheren Anteil an Annihilationen mit Valenzelektronen (kleinere Winkel bzw. geringere Doppler-Verschiebung). Diese Änderung der Kurvenform läßt sich durch den sogenannten S-Parameter ausdrücken. Dieser Parameter berechnet sich als das Flächenverhältnis einer in ihrer Begrenzung fixierten Zentralfläche und der Gesamtfläche. Sind nun die S-Parameterwerte für den defektfreien Zustand (Sb) und den Zustand der Probe bekannt, bei dem sich kompletter Positroneneinfang ergibt (Sv), so kann der Anteil der eingefangenen Positronen h und daraus die Positroneneinfangrate c berechnet werden:
![]() (8)
(8)
Allerdings hängt die Größe des gemessenen S-Parameters sowohl vom Defekttyp als auch von dessen Konzentration ab. Zur Ermittlung von h aus Winkelkorrelations- bzw. Doppler-Spektren sind daher weitgehende Modellannahmen nötig. Außerdem werden zur Ermittlung der Referenzwerte Sb und Sv in der Regel korrespondierende Lebensdauermessungen benötigt, so daß diese Techniken in der Regel ergänzend eingesetzt werden. Das ist insbesondere deshalb von Vorteil, da diese Impulsmethoden gegenüber der Lebensdauertechnik empfindlicher auf ihre chemische Umgebung reagieren (vgl. Kap. 6.5). Die Kombination aus der Lebensdauertechnik und den Impulstechniken bietet daher den optimalen Informationsgewinn.
Im Beispiel wurde das Trappingmodell für den Einfang an Leerstellen dargestellt. Dieses Modell gilt analog aber auch für andere Defekte, wie z. B. Versetzungen oder Leerstellenagglomerate.
Der Zusammenhang zwischen der auf die beschriebene Weise ermittelten Positroneneinfangrate c und der Defektkonzentration Cd hängt von der Art der Begrenzung des Einfanges in den Defekt ab. Für Leerstellen, Versetzungen und kleine Leerstellenagglomerate (n < 5) ist der Einfang übergangsratenbegrenzt, d. h. nicht die Diffusion zum Defekt, sondern die notwendige Energieabgabe beim Übergang des Positrons in den gebundenen Zustand ist der begrenzende Faktor für den Prozeß der Lokalisation. Hier gilt die einfache Beziehung:
![]() (9)
(9)
wobei µ, die spezifische Positroneneinfangrate ist, die für einen bestimmten Defekt eine Konstante darstellt, aber temperaturabhängig sein kann. Für ausgedehntere Defekte, wie große Leerstellenagglomerate und Ausscheidungen, ist der einfangbegrenzende Faktor die Diffusion zum Defekt. Für kugelförmige Defekte gilt dann:
![]() (10)
(10)
Dabei ist D+ die Diffusionskonstante der Positronen, r der Radius des Defektes und N seine Dichte. Mit diesen Beziehungen ist es nun möglich, die experimentell bestimmte Einfangrate c mit der Defektkonzentration zu verbinden, wenn zuvor die spezifische Einfangrate einmal durch ein unabhängiges Experiment bestimmt wurde. Bei einfachen Metallen ist diese Referenzmessung durch unterschiedliche Methoden leicht zu realisieren, wohingegen die Ermittlung der Leerstellenkonzentration in Verbindungshalbleitern mit alternativen Methoden oft nur als Größenordnungsabschätzung möglich ist.
Typische Werte für die spezifische Einfangrate sind µ1v=5 * 1014 s-1 für Leerstellen und µdisl = 1 cm2 s-1 für Versetzungen. Die Ermittlung dieser Werte ist mitunter kompliziert, da in vielen Fällen keine Methode zur Verfügung steht, mit der die Leerstellenkonzentration zu Vergleichszwecken bestimmbar ist. Allerdings sind gerade auf dem Gebiet der Verbindungshalbleiter in der letzten Zeit einige Fortschritte erreicht worden, so daß die Konzentrationen nun mit absoluten Fehlern von weniger als einer halben Größenordnung bestimmbar sind. Für kleine Leerstellenagglomerate (n<5) ergibt sich die spezifische Einfangrate aus der Rate für die entsprechenden Einfachleerstellen:
![]() (11)
(11)
n ist die Anzahl der fehlenden Atome im Leerstellenagglomerat. Mit den angegebenen spezifischen Einfangraten ergibt sich ein Empfindlichkeitsbereich der Methode für den Defektnachweis von etwa 10-6 bis 10-3 Leerstellen pro Atom und 109 bis 1012cm Linienlänge pro cm-3 für Versetzungen (Abb. 5).
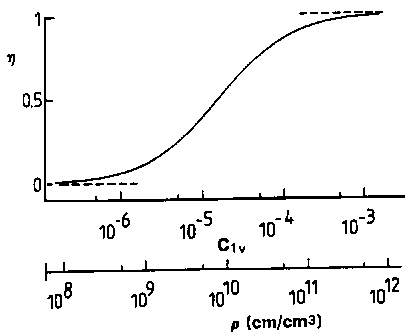
Abb. 5 Der Anteil der durch Defekte eingefangenen Positronen h in Abhängigkeit von der Konzentration von Einfachleerstellen (C1V) bzw. Versetzungen (r).
In Halbleitern ergeben sich gegenüber diesem einfachen Bild einige Besonderheiten. So können Leerstellen eine positive oder negative Ladung tragen, die ein langreichweitiges Coulomb-Potential bewirkt, das zur Abstoßung von Positronen (positive Ladung) oder zu deren zusätzlicher Anziehung (negative Ladung) führt (vgl. Abb. 2). Die spezifischen Einfangraten sind daher wie folgt zu erwarten: µ+ << µº < µ- . Damit muß die Gleichung (9) modifiziert werden:
![]() (12)
(12)
Dabei ist f der Anteil der Leerstellen, der negativ geladen ist, 1 - f der Anteil der neutralen Leerstellen. Positiv geladene Leerstellen wurden nicht berücksichtigt, da sie keine Positronen lokalisieren können (vgl. Kap. 3). Beim Auftreten von mehrfach geladenen Leerstellen ist Gl. (12) entsprechend zu modifizieren. Der Anteil f ergibt sich aus der Fermi-Dirac-Statistik:
![]() (13)
(13)
Dabei ist Ed - Ef der Abstand des Fermi-Niveaus vom Defektniveau, d. h. dem energetischen Niveau der Störstelle für den Übergang von der Neutralität zur negativen Ladung in der Bandlücke. g ist der Entartungsfaktor und kT das Produkt aus Boltzmann-Konstante und Temperatur.
Eine weitere Besonderheit stellt die Tatsache dar, daß die üblichen Versetzungsdichten in Halbleitern mit 0 <= r < 105 cm-2 deutlich unter der Empfindlichkeitsschwelle der Positronenannihilation liegen. Die Methode ist daher wegen ihrer Unempfindlichkeit gegen andere Defekte wie Fremdatome, Zwischengitteratome und Antistrukturbesetzungen speziell geeignet, leerstellenartige Defekte zu identifizieren.
Aus dem breiten Spektrum von Anwendungen der Methode sollen hier im wesentlichen einige Ergebnisse vorgestellt werden, die im Positronenlabor des Fachbereiches Physik der MLU erarbeitet wurden.
Leerstellen liegen im Festkörper im thermodynamischen Gleichgewicht mit einer bestimmten Konzentration vor [8]:
![]() (14)
(14)
SvB und EvB sind die Bildungsentropie und die Bildungsenergie der Leerstelle. Die Konzentration steigt mit wachsender Temperatur. Abb. 6 zeigt das Ergebnis eines Aufheizexperimentes einer polykristallinen Al-Scheibe. Bei niedrigen Temperaturen steigt der S-Parameter der Winkelkorrelationskurven zunächst linear an. Bei Temperaturen von 250 ºC hebt sich die Kurve s-förmig von dieser Geraden ab.
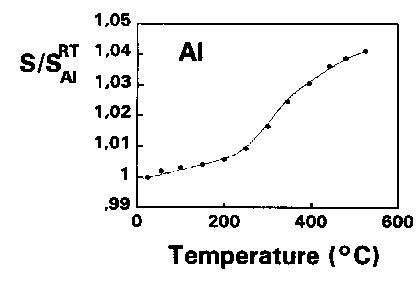
Abb. 6 Die auf den Raumtemperaturwert normierten S-Parameterwerte der Winkelkorrelationskurven einer polykristallinen Al-Probe in Abhängigkeit von der Temperatur [9].
Ursache für den linearen Anstieg ist die thermische Gitterausdehnung der Al-Probe. Bei höheren Temperaturen steigt die Konzentration der Leerstellen im thermischen Gleichgewicht nach Gl. (14) an. Es werden zunehmend Positronen in Leerstellen lokalisiert. Die Annihilation aus Leerstellen erfolgt mit einem größeren Anteil an Valenzelektronen, als es aus den ungestörten Kristallbereichen der Fall ist. Diese haben im Mittel einen geringeren Impuls, so daß kleine Winkel der Abweichung aus der Kollinearität bevorzugt werden. Damit steigt der S-Parameter über den linearen Anstieg der Gitterausdehnung an. Aus dem Anstieg kann die Positroneneinfangrate c bestimmt werden, und aus Arrhenius-Auftragungen läßt sich die Leerstellenbildungsenergie bestimmen. Dies wurde für eine große Zahl von Metallen und Legierungen durchgeführt und stellt eine Standardanwendung der Methode dar.
Bei Experimenten nahe dem Schmelzpunkt wurde eine Abweichung der Kurve vom einfachen Trappingmodell (Kap. 5) beobachtet, die als Auftreten von Doppelleerstellen im thermischen Gleichgewicht gedeutet und in quantitative Übereinstimmung mit theoretischen Modellen gebracht werden konnte.
Neben dem Studium von Gleichgewichtsdefekten spielt vor allem die Untersuchung von induzierten Defekten, ihrer Struktur und Konzentration sowie ihrer Ausheilkinetik eine große Rolle. In Metallen hat die plastische Deformation eine besondere Bedeutung. Auch hier eignet sich die Positronenannihilation zur Untersuchung dieser Defekte.
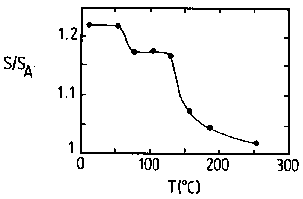
Abb. 7 Ergebnisse eines isochronen Ausheilexperimentes von deformiertem polykristallinen Al.
Abb. 7 zeigt das Ergebnis eines isochronen Ausheilexperimentes (0,2 K/min) von deformiertem Al [9]. Die Probe wurde bei Raumtemperatur (RT) durch Walzen 90% dickenreduziert, bei der angegebenen Temperatur wärmebehandelt und bei RT gemessen.
Nach der Deformation ist der auf den Al-Wert (defektfrei bei RT) normierte S-Parameter durch Positroneneinfang an den eingebrachten Defekten deutlich angestiegen. Die ersten Ausheiltemperungen vermindern bei etwa 100 ºC den S-Parameter auf ein zweites Plateau, das bei etwa 150 ºC endet. Der S-Parameter fällt dann schnell zu kleineren Werten und erreicht den Wert für defektfreies Al bei Temperaturen von etwa 300 ºC.
Die erste kleinere Ausheilstufe unter 100 ºC ist auf das Ausheilen von Leerstellen zurückzuführen, die bei der Versetzungsentstehung und Bewegung im Material verbleiben. Dies ist insofern überraschend, da bekannt ist, daß eingebrachte Überschußleerstellen in Al bereits unterhalb RT ausheilen. Aus dem Ergebnis kann man daher schlußfolgern, daß die Leerstellen an Verunreinigungsatome gebunden sind und dadurch bis zu höheren Temperaturen stabil sind. Diese Vermutung wurde durch Untersuchungen an verschiedenen schwach legierten Al-Legierungen bestätigt [18]. Insbesondere erweisen sich die relativ großen Mg-Atome als sehr effektive "Leerstellenfänger", da die freie Energie des Gitters durch die Verminderung der Deformationsenergie verringert wird. Durch isotherme Ausheilexperimente bei unterschiedlichen Temperaturen kann die Leerstellenbindungsenergie an die Fremdatome bestimmt werden.
Die Hauptausheilstufe stellt die Rekristallisation des stark gestörten Al-Gitters dar, in deren Verlauf die eingebrachten Versetzungen bis unter die Empfindlichkeitsschwelle der Positronenannihilation ausheilen. Es wird dann der S-Parameter für das defektfreie Al gemessen. Eventuell noch verbliebene Defekte werden durch die Positronen nicht nachgewiesen, weil ihre mittleren Abstände zu groß sind, wie z. B. neue Korngrenzen, oder weil Positronen generell nicht für sie empfindlich sind, wie Zwischengitteratome.
Wie im vorangegangenen Kapitel erläutert wurde, entstehen bei der plastischen Deformation von Metallen neben Versetzungen auch Punktdefekte, die bei Beginn der Ausheilung noch durch Fremdatome gebunden sein können. In Ni-Legierungen wurde das Ausheilverhalten näher untersucht und eine Besonderheit gefunden. Abhängig vom Typ des Legierungspartners wurde bei isochronen Aufheizexperimenten die Bildung von Leerstellenagglomeraten beobachtet [10, 11]. Dieser Effekt war bei Ni-Sb-Legierungen besonders ausgeprägt. In Abb. 8 wurden die Ergebnisse für Legierungen mit unterschiedlichem Sb-Gehalt dargestellt [11].
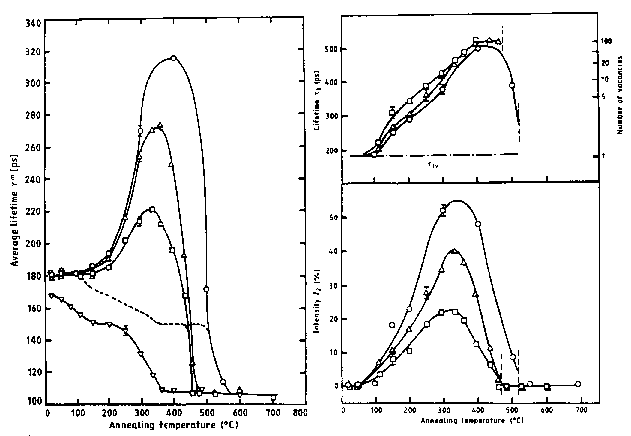
Abb. 8 Positronenlebensdauerresultate einer isochronen Ausheilbehandlung von 90% kaltgewalzten Ni-Sb-Legierungen mit unterschiedlichem Sb Gehalt (Dreiecke auf der Spitze: reines Ni, Vierecke: 0.03 at.%Sb und Kreise: 1 at.%Sb). Dreiecke: 0.1 at.%Sb)
Der Vergleich der mittleren Lebensdauern für reines Ni (5 N) und für die Ni-Sb (0,03 at.%)-Legierung zeigt bereits ein völlig unterschiedliches Verhalten. Die Kurve des reinen Metalls verläuft analog zur S-Parameterkurve für deformiertes Al (vgl. Kap. 6.2.). Zunächst heilen in den ersten Temperschritten bis etwa 150 ºC Leerstellen aus, bevor bei etwa 300 ºC die Rekristallisation des Materials einsetzt. Im Gegensatz dazu erhöht sich die mittlere Lebensdauer tm für die Legierung, erreicht Werte um 220 ps und fällt dann bei etwa 450 ºC steil ab. Die Ursache steht offensichtlich mit dem Gehalt an Sb in Verbindung, denn der Effekt verstärkt sich mit wachsender Sb-Konzentration. Das Maximum wird stärker ausgeprägt und erreicht Werte von 320 ps. Damit ist schon die mittlere Lebensdauer erheblich größer als der Wert für Versetzungen oder Leerstellen (tdisl = 170 ps, tv = 180 ps).
Die Ergebnisse der Zerlegung der Spektren in zwei Komponenten lassen die Ursachen erkennen (rechter Teil der Abb.). Die Lebensdauer t2 tritt nach Temperungen bei 100 ºC erstmalig auf (I2 wird größer Null) und erreicht Werte von 500 ps. Solche hohen Lebensdauerwerte treten in Metallen nur in Leerstellenagglomeraten auf. Modellrechnungen haben ergeben, daß sich die Lebensdauer im Bereich kleiner Agglomerate (n < 10) besonders stark ändert [12] (rechte obere Achse). Aus der Größe dieser Komponente läßt sich folglich auf die Größe des Leerstellenclusters schließen. Die drei Kurven für die verschiedenen Sb-Konzentrationen unterscheiden sich kaum, obwohl die Konzentration sich um eine Größenordnung ändert. die Größe der Cluster ändert sich daher für alle drei Legierungen analog und erreicht am Ende Werte von n > 50. Die Positronen annihilieren an den gebildeten "inneren Oberflächen". Die Lebensdauer ist für eine weitere Vergrößerung des Clusters nicht mehr empfindlich. Die Zahl dieser Cluster ist eine Funktion des Sb-Gehaltes der Legierung, wie die Unterschiede der Intensität I2 belegen. Eine weitere interessante Einzelheit ist die Tatsache, daß die Rekristallisation in der Legierung verzögert abläuft. Es ist eine Verschiebung dieser Temperatur um bis zu 200 K zu beobachten.
Ähnliche Effekte wurden für binäre Ni-Legierungen mit den relativ großen Atomen As, Pb und In gefunden. Schwächer war der Effekt für Zn und Ge, während kein Clustereffekt für die kleinen Ti-, Al- und W-Atome gefunden wurde. Diese Tendenz korreliert sehr gut mit den Werten der Fremdatom -Leerstellen -Bindungsenergie, wie sie sich aus dem Leerstellenmodell für das Schmelzen von Metallen ergeben (vgl. Diskussion in [11]).
Das Sintern ist durch die Schwindung des Volumens vom Sinterpulver zum Sinterkörper charakterisiert. Diese Schwindung wird in zwei Etappen realisiert. Zunächst werden größere Hohlräume durch kleinere Pulverteilchen aufgefüllt, wobei sich deren Form im wesentlichen nicht ändert. In der zweiten, für die angestrebten Materialeigenschaften wichtigeren Phase wird Material in den Pulverteilchen bewegt und füllt die verbliebenen kleinen Hohlräume des Sinterkörpers. Es wurde beobachtet, daß der Prozeß der Volumenschwindung bereits während der Aufheizphase trotz hoher Aufheizraten im wesentlichen abgelaufen ist. Der Materialtransport erfolgt daher nicht durch einfache Volumendiffusion (Nabarro -Herring -Mechanismus), da die beobachteten Diffusionskoeffizienten deutlich größer sind als die aus Tracer-Experimenten bekannten Volumendiffusionskoeffizienten. Offensichtlich verläuft die Diffusion defektunterstützt. Hierfür kommen beispielsweise Versetzungen in Frage, die sich in Oberflächennähe der abgleitenden Teilchen bilden. Ein solcher Bildungsmechanismus wurde an einkristallinen Kugel-Platte-Modellen nachgewiesen [13].
Die mögliche Rolle von Punktdefekten bei diesem Prozeß sollte durch Positronenexperimente untersucht werden. In Tablettenform hergestellte Preßlinge aus Ni- und Cu-Pulver wurden jeweils bis zu einer bestimmten Temperatur aufgeheizt, dann abgekühlt und anschließend wurde die Positronenlebensdauer bestimmt. Die Ergebnisse dieser Experimente ergaben sich analog für alle untersuchten Materialien und sollen stellvertretend am Beispiel der Sinterung von Ni-Pulver erläutert werden [14].
Die Schwindungsgeschwindigkeit epsilon zeigt zwei Maxima, die den oben erwähnten Prozessen der Teilchenbewegung und des Materialtransportes in den Teilchen entsprechen. Wenn nach dem Aufheizen die isotherme Sinterung beginnt (senkrechte Trennlinie), sind diese Prozesse weitgehend abgeschlossen. Die mittlere Positronenlebensdauer tm ist zu Beginn des Sinterprozesses mit etwa 170 ps deutlich gegenüber dem Volumenwert erhöht, was auf eine hohe Leerstellen- und Versetzungskonzentration des Preßlings schließen läßt. Dieser Wert erhöht sich bereits beim Beginn der Probenaufheizung. Während die zweite Komponente des Preßlings noch eine Lebensdauer von t2 = 190 ps aufwies (typischer Wert für Leerstellen 180 ps), erhöht sich dieser Wert schnell auf etwa 300 ps. Das weist auf Positroneneinfang durch Leerstellencluster (etwa 5 bis 10 Lehrstellen pro Cluster) hin. Diese Leerstellencluster, die sich beim Sintern gebildet haben, treten mit einer maximalen Konzentration von bis zu 1017 cm-3 auf. Interessant ist nun die Tatsache, daß sich diese Leerstellencluster gerade immer bei der Temperatur auflösen, bei der das zweite Schwindungsmaximum durch defektunterstützte Diffusion auftritt (im Beispiel zwischen 1000 und 1100 ºC).
Um eine zufällige Koinzidenz auszuschließen, wurde dieses Experiment mit unterschiedlichen Teilchengrößen, Aufheizraten und Pulvermaterialien wiederholt, wobei sich die Temperatur des zweiten Schwindungsmaximums um einige 100 K verschob. In jedem Fall korrelierte dieses Maximum mit der Auflösung der stets auftretenden Leerstellencluster. Die sich auflösenden Cluster hinterlassen eine große Zahl von Leerstellen. Diese sind nicht im thermischen Gleichgewicht und werden deshalb mit hoher Beweglichkeit ausheilen. Dieser Vorgang kann für die erhöhte Diffusion verantwortlich sein, da bekannt ist, daß sie über Leerstellen erheblich gesteigert wird. Auch kann die Möglichkeit in Betracht gezogen werden, daß diese Leerstellen über sich temporär bildende Leerstellenringe Versetzungen erzeugen, die dann ihrerseits zur erhöhten Diffusion beitragen.
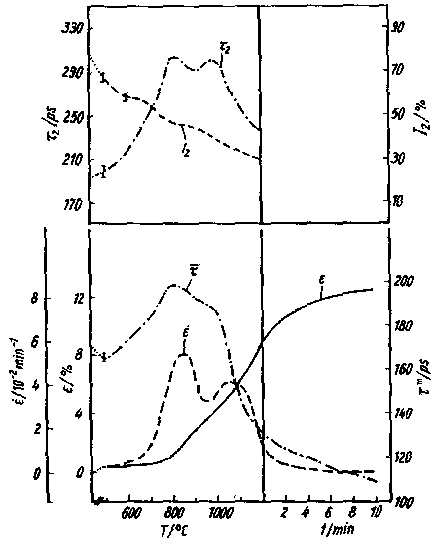
Abb. 9 Der Verlauf der Schwindung epsilon, der Schwindungsgeschwindigkeit epsilon', der mittleren Positronenlebensdauer tm und der Zweikomponentenzerlegung der Lebensdauerspektren (t2 und t2) beim Sinterversuch von Ni-Pulver (60% Anfangsdichte, Aufheizgeschwindigkeit 200 K/min und mittlere Teilchengröße 80 µm)
Aluminium ist nach Stahl der zweitwichtigste technische Werkstoff. Während reines Aluminium ein sehr duktiles Material ist, kann durch unterschiedliche Härtungsmechanismen eine Härte erreicht werden, die der von Stahl nahekommt. Besonders wichtig ist die Ausscheidungshärtung. Hierbei werden die sich durch das Material bewegenden Versetzungen durch viele kleine Ausscheidungen behindert [15].
Al-Zn ist eine intensiv untersuchte Modellegierung. Sie ist besonders interessant, weil hier viele metastabile Ausscheidungsstufen bis hin zur stabilen hexagonalen Zinkphase durchlaufen werden. Nach dem Abschrecken aus dem Löslichkeitsgebiet bilden sich zunächst zum Al-Wirtsgitter völlig kohärente Guinier-Preston-Zonen (GPZ), die bei höheren Temperaturen zur teilkohärenten rhomboedrischen a'R-Phase übergehen, bevor dann nach weiteren Umwandlungen die stabile h-Phase gebildet wird.
Für eine Al-Zn(10 at.%)-Legierung nach dem Homogenisieren bei 450 ºC und Abschrecken zu Raumtemperatur (RT) ist der Wert des Linienformparameters S/SAl deutlich kleiner (etwa 0,92) als der Parameter des ungestörten Wirtsmaterials (1,0), obwohl sich der Parameter beim Auftreten von Defekten mit offenem Volumen (z.B. Leerstellen) nur erhöhen kann. Der auf Al bezogene Raumtemperaturwert des Linienformparameters für Zn beträgt 0,905. Die Positronenlebensdauer bei RT liegt mit 155 ps ebenfalls deutlich unter dem Wert von defektfreiem Al (164 ps), aber nahe beim Wert für reines, defektfreies Zn. Die Erklärung für dieses ungewöhnliche Verhalten kann nur durch die Annahme des Positroneneinfangs durch die defektfreien, aber zinkreichen GPZ gegeben werden. Dies konnte in umfangreichen Untersuchungen an diesem Material und analog auch an der Legierung Al-Ag nachgewiesen werden [9]. Die Positronen werden nach ihrer Thermalisation bei der Diffusion durch das Kristallgitter durch GPZ eingefangen". Verantwortlich dafür ist die höhere Affinität der Positronen zu den Zn-Atomen, wodurch eine Potentialmulde entsteht, die zwar flach ist (in der Größenordnung von 1 eV oder kleiner), aber durch ihre erhebliche Ausdehnung (r etwa 1 bis 5 nm) gebundene Zustände für Positronen enthält. Diese werden dann in den GPZ lokalisiert, d.h., ihre Wellenfunktion ist auf das GPZ-Gebiet beschränkt. Die Annihilationsparameter spiegeln dann die chemische Zusammensetzung der Ausscheidung wider. So enthält die GPZ bei RT etwa 70 at.% Zn. Denselben Wert kann man aus den RT-Annihilationswerten von Al, Zn und Al-Zn(10 at.%) gewinnen, wenn man eine (geringe) Korrektur wegen der erhöhten Affinität zu den Zn-Atomen berücksichtigt.
Diese einmalige Fähigkeit der Methode, in den Ausscheidungen Leerstellen oder Versetzungen nachweisen zu können, wurde in einem Experiment zum Nachweis des Überganges von den vollkommen kohärenten GPZ zur teilkohärenten a'R-Phase einer Al-Zn(15 at.%)-Legierung ausgenutzt [16]. Dieser Übergang wird dann vollzogen, wenn beim Wachstum der GPZ eine kritische Größe erreicht wird, bei der die Spannungen durch die Gitterfehlanpassung zum Einschieben einer zusätzlichen Gitterebene in die Ausscheidung führt. Diese Ebene ist dann durch eine Anpaßversetzung umgeben, die eine sehr attraktive Positronenfalle darstellt.
Abb. 10 zeigt das Ergebnis einer isothermen Auslagerung dieses Materials bei 100ºC. Die Mikrohärte weist bei einer Auslagerungszeit von > 104 s einen drastischen Abfall auf, der auf den sich vollziehenden Übergang von den GPZ zur a'R-Phase hinweist. Ursache ist der Abbau des weitreichenden Spannungsfeldes um die gitterfehlangepaßten GPZ beim Einbau der Zusatzebene. Dadurch wird die Behinderung der Versetzungsbewegung verringert, die Härte sinkt. Bei demselben Auslagerungszustand beginnen die Teilchen schneller zu wachsen, wobei durch den zunehmenden Übergang zu einer ellipsoidalen Form der Ausscheidungen zwei Guinier-Radien auftreten (unterer Bildteil).
Die Annihilationsparameter weisen zu Beginn der Auslagerung Werte auf, wie sie für die defektfreien GPZ beobachtet wurden, t = 155 ps und S/SAl = 0,91. Wie oben erläutert, reflektieren diese Parameter die chemische Zusammensetzung der Ausscheidung. Beim Übergang der GPZ zu den a'R-Teilchen werden die erwähnten Versetzungen in der Peripherie der Ausscheidungen gebildet. Die Positronen werden nun mit großer Wahrscheinlichkeit in diesen Versetzungen bis zu ihrer Annihilation festgehalten. Dadurch sollten dann die Lebensdauer und der S-Parameter ansteigen, was experimentell auch gefunden wird (oberer Bildteil von Abb. 10). Die Zerlegung der Spektren in zwei Komponenten ergibt eine Lebensdauer im Defekt von etwa 240 ps, wie sie für Leerstellen oder Versetzungen in Al gefunden wurde, und bestätigt damit die Interpretation.
Die Ausscheidungsbildung in Al-Zn-Mg-Legierungen wurden ausführlich studiert. Im Gegensatz zu den Al-Zn- Legierungen wurden in den zinkreichen GPZ Leerstellen nachgewiesen [9, 17], die an ein Mg-Atom gebunden sein müssen und dort die mechanischen Spannungen verringern. Durch Alterungsexperimente von einigen Stunden bis zu 2 Jahren konnte nachgewiesen werden, daß diese Leerstellen auch noch bei Raumtemperatur in die GPZ eingebaut werden.
In Al-Si- und Al-Ge-Legierungen bilden sich ausschließlich, schon bei den Ausscheidungskeimen beginnend, inkohärente Teilchen. Dadurch wird die Grenzfläche zwischen Al-Matrix und Ausscheidung defektreich. Diese Defekte bilden Positronenhaftstellen. Die Keimbildungs- und Wachstumsprozesse konnten auf diese Weise mit Positronen ausführlich studiert werden [9, 19, 20].
Abb. 10 Die Annihilationsparameter tm, S/SAl, die Vickers-Mikrohärte und der Guinier-Radius der Ausscheidung ermittelt durch Röntgenkleinwinkelstreuung für die isotherme Auslagerung einer Al-Zn (15 at.%) Legierung nach dem Abschrecken von 450ºC zu RT.
Die eingangs erläuterten Techniken und Möglichkeiten der Methode der Positronenannihilation bewähren sich auch beim Studium von Kristalldefekten in Halbleitern. Jedoch ergeben sich einige Besonderheiten. So ist beispielsweise die Versetzungsdichte in Halbleitern mit bis zu 105 cm-2 zu gering, um einen merklichen Anteil der Positronen zu lokalisieren. Die Positronen können auch nicht durch Zwischengitteratome, Antistrukturdefekte, Dotierungsatome und andere auftretende Defekte gebunden werden (eine Ausnahme sind negativ geladene Defekte bei sehr tiefen Temperaturen [21]). Auch treten gewöhnlich Ausscheidungen nicht mit genügend hohen Dichten auf, so daß die Positronenannihilation in Halbleitern spezifisch empfindlich für Leerstellen ist. Diese Einschränkung stellt jedoch keinen Nachteil dar, da nun eine Methode gegeben ist, mit der ein wichtiger Defekttyp identifiziert werden kann. Dies ist um so bedeutender, da insbesondere in Verbindungshalbleitern kaum geeignete Methoden zur mikroskopischen Identifizierung von Punktdefekten existieren.
Eine weitere Besonderheit ist die bereits im Kap. 5.2. diskutierte Tatsache, daß in Halbleitern Leerstellen geladen sein können. Die spezifische Positroneneinfangrate µ, hängt aber wegen der positiven Ladung des Positrons vom Ladungszustand der Leerstellen ab. Damit ist eine direkte Möglichkeit des Studiums der Ladungsübergänge der Leerstellen und der Bestimmung der Defektniveaus in der Bandlücke gegeben [22].
In den Verbindungshalbleitern GaP und GaAs liegen nach der Züchtung offenbar stets P- bzw. As-Leerstellen vor, die mit Positronen untersuchbar sind, während keine Ga-Leerstellen nachzuweisen sind (vgl. Argumentation in [22]). Diese Phosphor- bzw. Arsen-Leerstellen haben ihre Umladungsniveaus in der oberen Hälfte der Bandlücke.
Nach Berechnungen werden jeweils drei Umladungsniveaus erwartet, die von einer positiven bis zu einer zweifach negativ geladenen Leerstelle führen sollen [23]. Um diese Umladungen auszuführen, muß das Fermi-Niveau des Halbleiters durch die obere Bandhälfte geschoben werden. Zur Demonstration wurden zwei unterschiedliche Wege beschritten.
Die Lage des Fermi-Niveaus ist temperaturabhängig. Eine Temperaturerhöhung führt bei einer n-leitenden Probe zur Absenkung des Fermi-Niveaus von der oberen Bandkante in Richtung Bandmitte. Die Ergebnisse eines entsprechenden Experimentes sind in Abb. 11 (obere Kurve) dargestellt [24].
Abb. 11 Die mittlere Positronenlebensdauer in Abhängigkeit von der Lage des Fermi-Niveaus für P-Leerstellen in GaP.
Der Positroneneinfang nimmt mit zunehmendem Abstand des Fermi-Niveaus von der oberen Bandkante ab. Dieser Prozeß verläuft reversibel. Ursache ist die Umladung der Phosphorleerstellen zu einem positiveren Ladungszustand, was durch eine Verringerung der spezifischen Positroneneinfangrate zur Absenkung der Positronenlebensdauer führt. Eine numerische Auswertung der Daten ergibt eine energetische Lage des Defektniveaus von Ec - Ed = 270 meV.
Eine zweite Möglichkeit, das Fermi-Niveau zu verschieben, besteht in der Erzeugung tiefer Zentren, die die verfügbaren Elektronen aufnehmen. Solche Zentren entstehen als Eigendefekte beim Wachstum, beim Dotieren und können aber auch durch Defekte eingebracht werden. So ist bekannt, daß durch Elektronenbestrahlung n-leitende Proben in den halbisolierenden Zustand überführt werden können. Dabei bewegt sich das Fermi-Niveau von der Leitungsbandkante bis in die Bandmitte. Dieser Effekt wurde für die untere Kurve in Abb. 11 ausgenutzt. Wieder wird deutlich, daß sich mit absinkendem Fermi-Niveau der Positroneneinfang verringert. Die Daten können mit dem gleichen energetischen Niveau für die Defektumladung erklärt werden, wie es sich auch aus der Temperaturabhängigkeit ergab. Parallel durchgeführte Hall-Messungen erlauben die Bestimmung der Lage des Fermi- Niveaus. Aus temperaturabhängigen Hall-Messungen konnte weiterhin auf die in der oberen Bandhälfte vorhandenen elektrisch aktiven (umladbaren) Defekte geschlossen werden. Es wurden nur Niveaus bei 73 und 230 meV mit Konzentrationen von etwa 1016 cm-3 gefunden. Während das Niveau bei 73 meV eindeutig der Si-Dotierung zugeordnet werden kann, handelt es sich bei dem Niveau bei 230 meV um einen nicht näher bestimmten Eigendefekt. Der Vergleich mit den Positronenergebnissen legt nun den Schluß nahe, daß es sich hierbei um die P-Leerstellen handelt. Ein weiterer Beleg für die Richtigkeit dieser Annahme ist das analoge Ausheilverhalten dieser beiden Defekte. Das Positronensignal der Leerstelle verschwindet bei einer Temperung bei etwa 700 ºC in Übereinstimmung mit der Verringerung der Defektkonzentration, die aus den Hall-Messungen bestimmt wurde.
Abb. 12 Die Infrarot-Absorption und die Annihilationsparameter für halbisolierende GaAs-Kristalle in Abhängigkeit der Temperatur. Die Proben wurden vor dem Experiment bei der tiefsten Temperatur mit Protonen von hv = 1.2 eV bestrahlt.
Neben vergleichbaren temperaturabhängigen Messungen an GaAs-Einkristallen, die zur Schlußfolgerung eines Umladungsniveaus bei 120 meV führten [25], interessierte bei diesem Material vor allem der sogenannte EL2-Defekt. Dieser Eigendefekt stellt ein tiefes Zentrum dar und führt zur technologisch sehr bedeutenden Selbstkompensation des Materials. Obwohl bereits umfangreiche experimentelle und theoretische Untersuchungen zur mikroskopischen Struktur dieses Defektes vorgenommen wurden, ist diese Struktur noch nicht völlig geklärt [26]. Es scheint sicher, daß ein AsGa-Antistrukturdefekt Bestandteil der Defektstruktur ist. Momentan werden vor allem zwei Theorien diskutiert. Es wurde ein Modell vorgeschlagen, nach dem der EL2-Defekt mit dem AsGa-Defekt identisch sein soll [27]. Ein anderes Model [28] interpretiert den Defekt als AsGa-Asi-Komplex. Interessant ist nun, daß der EL2- Defekt bei tiefen Temperaturen (T < 115 K) durch Photonen in einen metastabilen Zustand überführt werden kann. Dieser Zustand ist dadurch gekennzeichnet, daß die typische Infrarot-Absorption (IR) des EL2-Defektes verschwindet und er auch durch keine andere Methode mehr nachweisbar ist. Bei einer Erhöhung der Temperatur über den kritischen Wert restauriert sich der EL2-Defekt mit seinen ursprünglichen Eigenschaften. Beide Modelle erklären diese metastabile Struktur unterschiedlich. Während das erste Modell einen Übergang AsGa <-> Asi-VGa annimmt, wird durch das zweite Modell lediglich eine metastabile Verrückung eines As-Atoms im Komplex AsGa-Asi angenommen. Das erste Modell erwartet im metastabilen Zustand, im Gegensatz zum zweiten Modell, eine Leerstelle. Damit ist die Positronenannihilation als Entscheidungshilfe geeignet.
Ein entsprechendes Experiment wurde mit einem Kryostaten durchgeführt, der auch IR-Absorptionsmessungen gestattete [29]. Zunächst wurde das metastabile Verhalten mit IR-Absorptionsmessungen geprüft (Abb. 12, oberer Bildteil). Die Probe wurde zu tiefen Temperaturen abgekühlt und mit Photonen bestrahlt (hv = 1,2 eV). Wie oben erläutert, weist die verringerte Absorption auf den Übergang zur metastabilen Konfiguration hin. Beim Erwärmen der Probe über die kritische Temperatur wird das ursprüngliche Absorptionsverhalten wieder hergestellt, der EL2-Defekt liegt mit seiner stabilen Konfiguration vor. Vergleichende Messungen mit Positronen zeigen deutlich, daß im metastabilen Zustand ein Leerstellensignal detektiert wird, das beim Übergang zur stabilen Konfiguration verschwindet. Die Höhe dieses Signals, d. h. der Anstieg der Lebensdauer, ist abhängig von der EL2-Konzentration. Er beträgt 2 ps für eine EL2-Konzentration von 1 * 1016 cm-3 und 5 ps für eine Konzentration von 2,5 * 1016 cm-3. Die Messung der Temperaturabhängigkeit des Positroneneinfanges (nicht dargestellt) läßt außerdem den Schluß zu, daß die Leerstelle selbst oder ihre unmittelbare Umgebung negativ geladen sein müssen. Damit sind die Ergebnisse in guter Übereinstimmung mit dem in [27] vorgestellten Modell.
In den schmallückigen Halbleitern dieser Gruppe, wie z. B. HgCdTe, spielen Hg-Leerstellen eine dominierende Rolle. Sie wirken als Akzeptoren und können u.U. das elektrische Verhalten bestimmen, da sie mit Konzentrationen bis zu 1019 cm-3 auftreten. Eine weitere Besonderheit ist, daß diese Leerstellenkonzentration auch noch nach der Züchtung durch Temperung bei einem bestimmten Dampfdruck der jeweiligen Komponente definiert eingestellt werden kann. Dies wurde ausgenutzt, um die Empfindlichkeit der Positronenmethode nachzuweisen und die spezifische Einfangrate für diesen Defekt zu bestimmen [30].
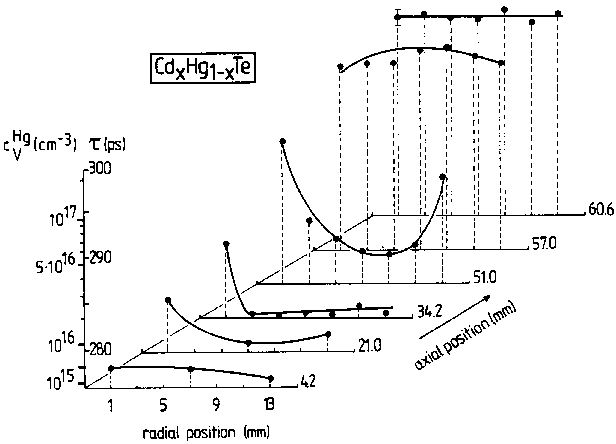
Abb. 13 Die Hg-Leerstellenverteiiung eines kompletten, aufgeschnittenen, THM-gezüchteten Hd1-xCdxTe-Einkristalls. Die Defektkonzentration wurde der gemessenen Positronenlebensdauer zugeordnet.
Hg1-xCdxTe wurde ausführlich und systematisch untersucht. Nach den oben erwähnten Temperuntersuchungen unter definierten Hg-Dampfdruckbedingungen wurden die gewonnenen Erfahrungen bei der Untersuchung von THM- gezüchteten Kristallen eingesetzt (THM = travelling heater method). Ein kompletter Kristall (c = 0,22) mit einer Länge von 65 mm und einem Durchmesser von 15 mm wurde in 1 mm dicke Scheiben geschnitten, die oberflächlich poliert und geätzt wurden. Abb. 13 zeigt das Ergebnis der Positronenuntersuchungen.
Die Defektkonzentration konnte nach den erwähnten Vorexperimenten der Hg-Leerstellenkonzentration zugeordnet werden (Ordinate). In den anderen beiden Dimensionen der Abbildung wurde die Position in einer Mittelebene des Kristalls dargestellt. Die Abbildung entstand aus sechs radial untersuchten Scheiben.
In den ersten Scheiben (Keimnähe) des Kristalls ist die Leerstellenkonzentration gering, die Lebensdauer der Positronen entspricht in etwa dem Wert für den defektfreien Kristall. Dies ändert sich in den letzten 15 mm des gezüchteten Kristalls. Die Leerstellenkonzentration steigt ieben, besteht in der Erzeugung tiefer Zentren, die die verfügbaren Elektronen aufnehmen. Solche Zentren entstehen als Eigendefekte beim Wachstum, beim Dotieren und können aber auch durch Defekte eingebracht werden. So ist bekannt, daß durch Elektronenbestrahlung n-leitende Proben in den halbisolierenden Zustand überführt werden können. Dabei bewegt sich das Fermi-Niveau von der Leitungsbandkante bis in die Bandmitte. Dieser Effekt wurde für die untere Kurve in Abb. 11 ausgenutzt. Wieder wird deutlich, daß sich mit absinkendem Fermi-Niveau der Positroneneinfang verringert. Die Daten können mit dem gleichen energetischen Niveau für die Defektumladung erklärt werden, wie es sich auch aus der Temperaturabhängigkeit ergab. Parallel durchgeführte Hall-Messungen erlauben die Bestimmung der Lage des Fermi- Niveaus. Aus temperaturabhängigen Hall-Messungen konnte weiterhin auf die in der oberen Bandhälfte vorhandenen elektrisch aktiven (umladbaren) Defekte geschlossen werden. Es wurden nur Niveaus bei 73 und 230 meV mit Konzentrationen von etwa 1016 cm-3 gefunden. Während das Niveau bei 73 meV eindeutig der Si-Dotierung zugeordnet werden kann, handelt es sich bei dem Niveau bei 230 meV um einen nicht näher bestimmten Eigendefekt. Der Vergleich mit den Positronenergebnissen legt nun den Schluß nahe, daß es sich hierbei um die P-Leerstellen handelt. Ein weiterer Beleg für die Richtigkeit dieser Annahme ist das analoge Ausheilverhalten dieser beiden Defekte. Das Positronensignal der Leerstelle verschwindet bei einer Temperung bei etwa 700 ºC in Übereinstimmung mit der Verringerung der Defektkonzentration, die aus den Hall-Messungen bestimmt wurde.
Abb. 12 Die Infrarot-Absorption und die Annihilationsparameter für halbisolierende GaAs-Kristalle in Abhängigkeit der Temperatur. Die Proben wurden vor dem Experiment bei der tiefsten Temperatur mit Protonen von hv = 1.2 eV bestrahlt.
Neben vergleichbaren temperaturabhängigen Messungen an
GaAs-Einkristallen, die zur Schlußfolgerung eines Umladungsniveaus bei
120 meV führten [25], interessierte bei diesem
Material vor allem der sogenannte EL2-Defekt. Dieser Eigendefekt stellt ein
tiefes Zentrum dar und führt zur technologisch sehr bedeutenden
Selbstkompensation des Materials. Obwohl bereits umfangreiche experimentelle
und theoretische Untersuchungen zur mikroskopischen Struktur dieses Defektes
vorgenommen wurden, ist diese Struktur noch nicht völlig geklärt
[26]. Es scheint sicher, daß ein
AsGa-Antistrukturdefekt Bestandteil der Defektstruktur ist. Momentan
werden vor allem zwei Theorien diskutiert. Es wurde ein Modell vorgeschlagen,
nach dem der EL2-Defekt mit dem AsGa-Defekt identisch sein soll
[27]. Ein anderes Model [28]
interpretiert den Defekt als AsGa-Asi-Komplex.
Interessant ist nun, daß der EL2- Defekt bei tiefen Temperaturen (T <
115 K) durch Photonen in einen metastabilen Zustand überführt werden
kann. Dieser Zustand ist dadurch gekennzeichnet, daß die typische
Infrarot-Absorption (IR) des EL2-Defektes verschwindet und er auch durch keine
andere Methode mehr nachweisbar ist. Bei einer Erhöhung der Temperatur
über den kritischen Wert restauriert sich der EL2-Defekt mit seinen
ursprünglichen Eigenschaften. Beide Modelle erklären diese
metastabile Struktur unterschiedlich. Während das erste Modell einen
Übergang AsGa <-> Asi-VGa annimmt,
wird durch das zweite Modell lediglich eine metastabile Verrückung eines
As-Atoms im Komplex AsGa-Asi angenomme. WENDROCK: Cryst. Res.
Technol. 20 (1985) 1495.
[17] DLUBEK, G., R. KRAUSE, O. BRÜMMER, F. PLAZAOLA: J.
Mat. Science 21 (1986) 853.
[18] DLUBEK, G., W. GERBER, A. VEHANEN, J. YIL-KAUPPILA:
Krist. & Technik 15 (1980) 1409.
[19] KRAUSE, R., G. DLUBEK, O. BRÜMMER, S.
SKLADNIEKIEWITZ, H. DAUT: Cryst. Res. Technol. 20 (1985) 267.
[20] DLUBEK, G., O. BRÜMMER, P. HAUTOJÄRVI: Acta
metall. 34 (1986) 66.
[21] SAARINEN, K., P. HAUTOJÄRVI, A. VEHANEN, R.
KRAUSE, G. DLUBEK: Phys. Rev. B 39 (1989) 5287.
[22] DLUBEK, G., R. KRAUSE: phys. stat. sol. (a) 102 (1987)
443.
[23] PUSKA, M.: J. Cond. Matter 1 (1989) 7347.
[24] KRAUSE, R., A. POLITY, W. SIEGEL, G. KÜHNEL.: Wird
zur Veröffentlichung vorbereitet.
[25] KRAUSE, R., A. POLITY, G. DLUBEK, K. FRIEDLAND, R.
RENTZSCH, W. SIEGEL., G. KÜHNEL: Positron Annihilation, Singapore, New
Yersey, Hong Kong 1989, S. 721.
[26] MANASREH, M. O., D. W. FISCHER, W. C. MITCHEL: phys.
stat. sol. (b) 154 (1989) 11.
[27] DABROWSKI, J., M. SCHEFFLER: Phys. Rev. B 40 (1989)
10391, und D. J. CHADI, K. J. CHANG: Phys. Rev. Lett. 60 (1988) 2187.
[28] VON BARDELEBEN, H. J., D. STIÉVENARS, D.
DERESMES, A. HUBER, J. C. BOURGOIN: Phys. Rev. B 34 (1986) 7192.
[29] KRAUSE, R., K. SAARINEN, P. HAUTOJÄRVI, A. POLITY,
G. GÄRTNER, C. CORBEL: Phys. Rev. Letters 65 (1990) 3329.
[30] KRAUSE, R., A. KLIMAKOW, F. M. KIESSLING, A. POLITY, G.
GILLE, M. SCHENK: J. Cryst. Growth 101 (1990) 512.
Manuskripteingang: 16. 5. 1991, HTML-Version 1/97
Verfasser:
Dr. REINHARD KRAUSE (E-Mail)
Dr. ANGELIKA POLITY (E-Mail)
zurück zu Kapitel 4.1