Activities of regular solutions

5.12 Activities of regular solutions

Completely analogous to the concept of effective mass which allows to incorporate non-idealities like lattice periodic potentials into the model of free electrons non-ideal mixtures are described by replacing molar fractions \(x_A\) and \(x_B\) by activities \(a_A\) and \(a_B\) (respectively activity coefficients \(a_A = \gamma_A x_A\) and \(a_B =\gamma_B x_B\)) but choosing the same functionality as for the ideal case in Eq. (5.6) for free particles (the ideal gas), i.e.

\begin{equation*} \begin{split} \Delta_{mix}G_m & = \Delta_{mix}G_m^{id} + G_m^{ex} = R T \left(x_A \ln a_A + x_B R\,T\, \ln a_B \right) \\ & = R\, T\, \left(x_A \ln x_A + x_B \ln x_B + x_A \ln \gamma_A + x_B \ln \gamma_B\right) \quad . \end{split} \label{dG_mix_3} \end{equation*}

(5.37)

Thus for the excess Gibbs molar energy we find

\begin{equation*} G_m^{ex} = R\, T\, \left(x_A \ln \gamma_A + x_B \ln \gamma_B \right) \label{dG_mix_ex_1} \quad. \end{equation*}

(5.38)

Particle interaction in regular solutions can e.g. be described by

\begin{equation*} \ln \gamma_A = \beta x_B^2 \quad \mbox{and} \quad \ln \gamma_B = \beta x_A^2 \quad, \end{equation*}

(5.39)

\begin{equation*} \mbox{so}\qquad G_m^{ex} = R\, T\, \left(x_A \beta x_B^2 + x_B \beta x_A^2 \right) = R\, T\, \beta x_A x_B \left(x_B+ x_A \right) = R\, T\, \beta x_A x_B = \Omega\, x_A x_B = H_m^{ex} \label{dG_mix_ex_2} \quad. \end{equation*}

(5.40)

Quite obviously \(\Omega\, x_A x_B\) is the most simple energy functionality for an interaction A-B. As very important consequences we find

Figure 5.10: Partial pressures for several \(\beta\).

\begin{equation*} a_A = \gamma_A x_A = x_A e^{\beta(1-x_A)^2} \quad, \end{equation*} (5.41)

i.e. a typical dependence of the activity on \(x_A\)
\begin{equation*} p_A = p_A^* a_A = p_A^*x_A e^{\beta(1-x_A)^2} \quad. \label{p_A_regular} \end{equation*} (5.42)

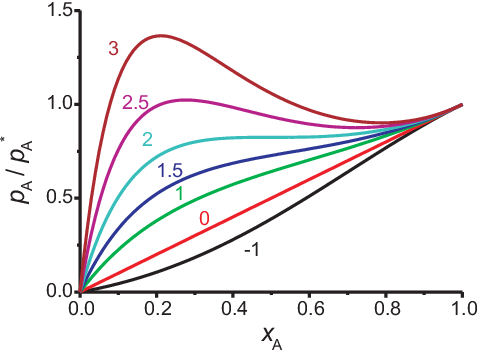
Fig. 5.10 shows results of Eq. (5.42) for several values of \(\beta\). For \(x_A \approx 1\) it demonstrates the typical deviation from Raoult’s law and shows that Raoult’s law is valid for \(\beta = 0\) and for all curves when \(x_A \rightarrow 1\) (pure state). For \(x_A \rightarrow 0\) we find Henry’s law where \(K_A\) depends strongly on \(\beta\).

Figure 5.11: Examples for partial pressures of mixtures: a) mixing of similar components; b) mixing of dissimilar liquids.

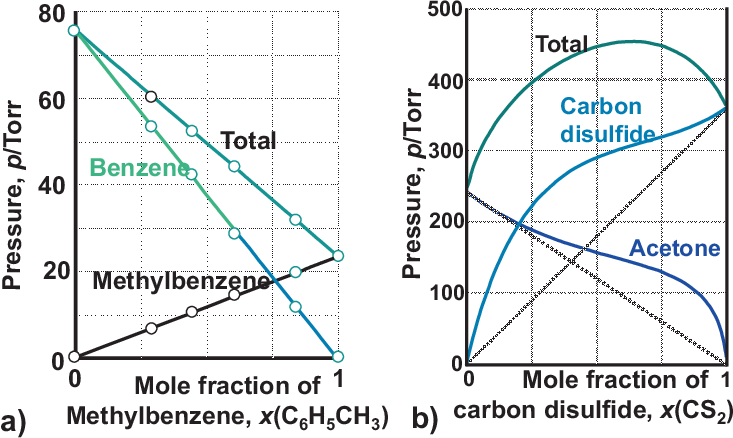
Typical mixing effects for the partial pressures are shown in Fig. 5.11:

In Fig. 5.11 a) no deviation from average values are found for highly related components, i.e. A-A \(\approx\) B-B \(\approx\) A-B. Thus ideal behavior is found.
In Fig. 5.11 b) shows an example for a positive deviation from Raoult’s law: \(p(mix)\) is larger than for an ideal solution, i.e. the intermolecular forces A-B are weaker than A-A and B-B; in this example the CS\(_2\) disturbs the H-bonding in acetone (keto-enol-tautomerism).
Strong deviations can also occur when dissociation (increases number of particles) or association (decreases number of particles) of the solute occurs, leading to an entropy contribution to mixing.