Raoult and Henry law for activity and fugacity

5.11 Raoult and Henry law for activity and fugacity

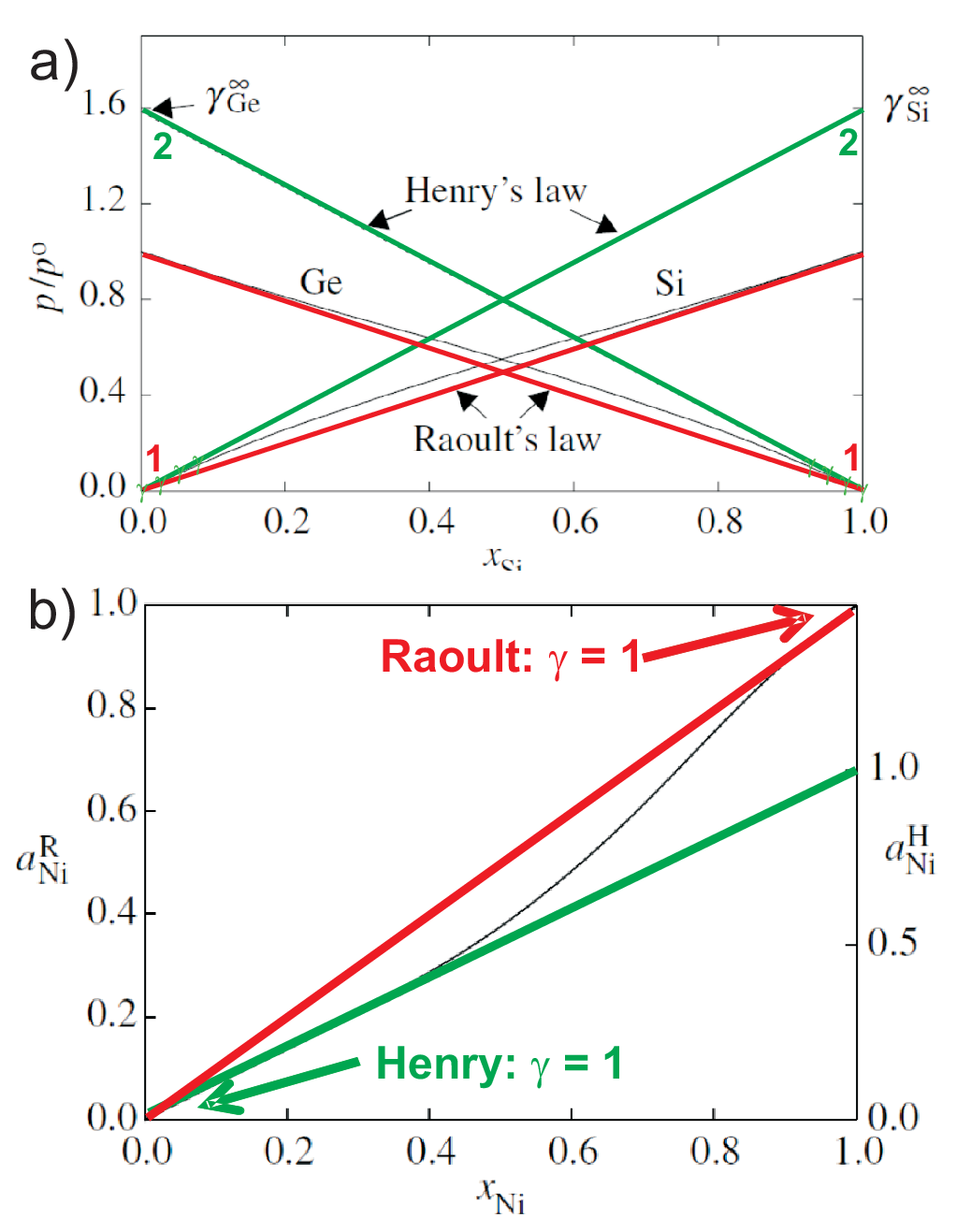
As discussed above the definition of the ideal state differs for solvent and solute; correspondingly the deviation from ideality differs for both components. As an example we discuss the \(p-x\) phase diagram shown in Fig. 5.8 a).

Figure 5.8: a) The vapor pressure above molten Si–Ge at 1723 K; b) the activity of Ni of molten Fe–Ni at 1850 K using Raoult and Henry standard state.

For the vapor pressure of solutions we find

(red) curves: Raoult’s law for the solvent (standard: pure component) \(p_A = x_A p_A^*\).
(green) curves: Henry’s law for the solute (extrapolated from low concentrations of the solute to \(x_B = 1\), hypothetical state) \(p_B = x_B K_B\), where \(K_B\) is the Henry constant. The Henry constant is large for highly volatile components.

So Henry’s and Raoult’s law have in common that they describe a linear behavior of the vapor pressure of the component under consideration (solute and solvent, respectively) and the mole fraction (or activities or fugacities).
Next we discuss a fundamental relation between Raoult (”R”) and Henry (”H”) standard state for the example of activities.

For the Raoult standard state we have

\begin{equation*} \mu_A^R = \mu_A^* \qquad \left( \gamma_A^R \right)_{x_A \rightarrow 1} = \left( \frac{a_A^R}{x_a} \right)_{x_A \rightarrow 1} =1 \label{eq:Raoult_standard} \end{equation*}

(5.31)

In Fig. 5.8 a) this corresponds to the properties of pure Si which slightly changes when adding small fractions of Ge, resp. to the properties of pure Ge which slightly changes when adding small fractions of Si. For pure Si all Si atoms are surrounded by Si atoms; adding small fractions of Ge will change slightly the surrounding of Si atoms with a corresponding change in \(\mu\).

Figure 5.9: Diagrams of activity and activity coefficients for a) Raoult’s law, b) Henry’s law.

For the Henry standard state we have

\begin{equation*} \mu_B^H = \mu_B^* \qquad \left( \gamma_B^H \right)_{x_B \rightarrow 0} = \left( \frac{a_B^H}{x_B} \right)_{x_B \rightarrow 0} =1 \label{eq:Henry_standard} \end{equation*}

(5.32)

In Fig. 5.8 a) this corresponds to the properties of tiny fractions of Si added to nearly pure Ge. So all Si atoms will be completely surrounded by Ge atoms. This is the standard state for the Henry model which is reflected in \(\mu^*\).

Combining both equations we find

\begin{equation*} \begin{split} \mu_k &=\;\; \mu_k^R + R\, T\, \ln a_k^R = \mu_k^H + R\, T\, \ln a_k^H\\ \Rightarrow \frac{a_k^R}{a_k^H} &=\;\; \exp \left[- \frac{\mu_k^R - \mu_k^H}{R\,T} \right] = const\\ \mbox{with} &\qquad \frac{a_B^R}{a_B^H} = \frac{a_B^R}{a_B^H} \frac{x_B}{x_B} = \frac{\gamma_B^R}{\gamma_B^H} = const\\ \mbox{or} &\qquad \ln \gamma_B^R = \ln \gamma_B^H + \ln (const)\\ \end{split} \label{eq:Raoult_Henry_standard} \end{equation*}

(5.33)

This is illustrated in Fig. 5.8 b) on a linear scale, and implies a constant offset on a logarithmic scale.

In what follows we will get more quantitative results for the Henry as well es for the Raoult law from discussing the properties of the vapor phase above the liquid solution. Since the vapor and the liquid phase are in thermodynamic equilibrium we find for the chemical potentials

\begin{equation*} \begin{split} \mu_B(l) = \mu_B(g) = \mu_B^0(g) + R\,T\, \ln \frac{f_B}{f^0} =& \;\; \mu_B^0(g) + R\,T\,\ln \frac{K_B}{f^0} + R\,T\,\ln x_B\\ &\mbox{since} \quad \lim_{x_B \rightarrow 0} f_B = p_B = K_B\, x_B \end{split} \label{eq:mu_Henry} \end{equation*}

(5.34)

So Henry’s law describes the equilibrium condition for an ideal dilute system which is a hypothetical state in which the pure solute approximates the state of infinite dilution, i.e. the ”ideal dilute”.

\begin{equation*} \begin{split} \mbox{Defining} &\qquad \mu_B^H= \mu_B^{\infty} = \mu_B^0(g) + R\,T\,\ln \frac{K_B}{f^0}\\ \mbox{we get for}\;\; x_B\rightarrow 0 & \qquad \mu_B(l) = \mu_B^{\infty} + R\,T\, \ln x_B\\ \mbox{and in general} &\qquad \mu_B(l) = \mu_B^{\infty}+ R\,T\, \ln x_B + R\,T\, \ln \gamma_B^H\\ \mbox{i.e.}&\qquad \lim_{x_B \rightarrow 0} \gamma_B^H = 1\\ \end{split} \label{eq:activity_Henry} \end{equation*}

(5.35)

These results are illustrated in Fig. 5.8 b).
For Raoult’s law we perform the same calculation

\begin{equation*} \begin{split} \mu_A^*(g) &=\;\; \mu_A^*(l) + R\,T\,\ln a_A \quad \mbox{with}\quad a_A = \gamma_A x_A \\ \Rightarrow \left(\frac{\partial \mu_A^*(g)}{\partial p}\right)_T &=\;\; \left(\frac{\partial \mu_A^*(l)}{\partial p}\right)_T + R\,T\, \left(\frac{\partial \ln a_A}{\partial p}\right)_T \\ \Rightarrow R\,T\, \left(\frac{\partial \ln a_A}{\partial p}\right)_T &=\;\; \left(\frac{\partial \mu_A^*(g)}{\partial p}\right)_T - \left(\frac{\partial \mu_A^*(l)}{\partial p}\right)_T = V_{A,m}^*(g) - V_{A,m}^*(l) \approx V_{A,m}^*(g) \\ \Rightarrow R\,T\, d\ln a_A = V_{A,m}^*(g) dp &=\;\; R\,T\, \frac{dp}{p} = R\,T\, d\ln p \quad \mbox{assuming ideal vapor}\\ \Rightarrow \int_1^{a_A} d\ln a_A &=\;\; \int_{p_A^*}^{p_A} d\ln p \quad \Rightarrow \quad a_A = \frac{p_A}{p_A^*}= \gamma_A x_A \approx x_A \end{split} \label{eq:activity_Raoult} \end{equation*}

(5.36)

These results are illustrated in Fig. 5.9 a). So if the solvent is much more volatile than the solute one can easily quantify activities by vapor pressure measurements at constant temperature. As an example we discuss 0.5 M KNO\(_3\) at 100 \(^{\circ}\)C. The vapor pressure is measured as 99.95 kPa, thus, the activity of water \(a_{H_2O}\) in the solution is: \(a_A\) =(99.95 kPa/101.325 kPa) = 0.9864.