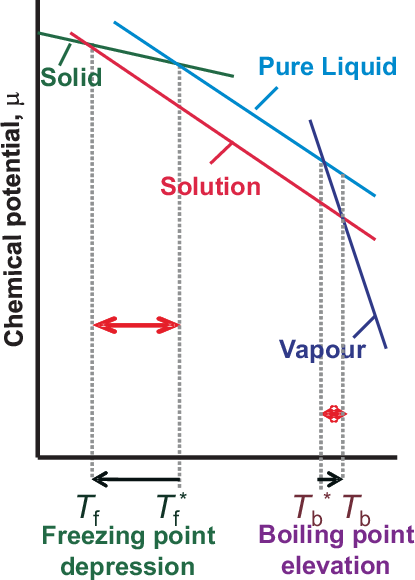
Colligative properties of ideal systems

5.13 Colligative properties of ideal systems

Colligative properties depend only on the number of particles, not on their chemical nature. In any case the chemical potential of a component is reduced with respect to its pure state, since for small addition of a second component the entropy increase will be significant. We will calculate the elevation of boiling point (b.p.) in two steps:

change of chemical potential of liquid state

\begin{equation*} \mu_A^*(g)=\mu_A(g)=\mu_A(l)=\mu_A^*(l)+R\,T\, \ln x_A = \mu_A^*(l)+R\,T\, \ln (1-x_B) \approx \mu_A^*(l)- R\,T\, x_B \label{eq:dmu_A_mix} \end{equation*} (5.43)

In this calculation we assumed an ideal behavior of A and a solute which is not vaporized.

Relating the change in composition and chemical potential to the resulting change in the boiling point is

\begin{equation*} \begin{split} \mu_A^*(g) &=\;\; \mu_A^*(l)- R\,T\, x_B \quad \Rightarrow \quad - x_B = \frac{\mu_A^*(g)- \mu_A^*(l)}{R\,T}\\ \Rightarrow -\frac{d x_B}{dT} &=\;\; \frac{1}{R} \frac{d\left(\Delta_{vap}G_m/T\right)}{dT} = - \frac{\Delta_{vap} H}{R\,T^2}\\ \Rightarrow \quad \int_0^{x_B} d x_B &=\;\; \int_{T^*}^{T} \frac{\Delta_{vap} H}{R\,T^2} dT \quad \Rightarrow \quad x_B = \frac{\Delta_{vap} H}{R}\left(\frac{1}{T^*}-\frac{1}{T} \right)\\ \Rightarrow \quad x_B &\approx\;\; \frac{\Delta_{vap} H}{R} \frac{\Delta T}{T^{*2}} \quad \mbox{or} \quad \Delta T = \frac{R\,T^{*2}}{\Delta_{vap} H} x_B = B\, x_B \quad \mbox{$B$: boiling point constant}\\ \end{split} \label{eq:dT_A_mix} \end{equation*}

(5.44)

Figure 5.12: Principle of boiling point elevation and freezing point depression.

here $T^*$ and $T$ are the boiling points of pure A and A in mixture. Additionally in the last line we assumed that $T^*$ and $T$ do not deviate strongly so that a Taylor expansion up to linear order is enough to linearize the $1/T$ difference. In essence the boiling point elevation of the mixture will be larger if the boiling point of the solvent is high. Fig. 5.12 summarizes these results and shows in addition the depression of the freezing point to exactly the same mechanism.
To calculate the boiling point elevation for solutions of salts a correction is needed, since e.g. NaCl dissociates into two ions in solution

\begin{equation*} \begin{split} \Delta T &=\;\; 2\, B\, x_{NaCl} = 2\, B\, \frac{n_{NaCl}}{n_{H_2O}+n_{NaCl}} \approx 2\, B\, \frac{n_{NaCl}}{n_{H_2O}}\\ &\approx \;\; 2\, B \frac{m_{NaCl}/M_{NaCl}}{m_{H_2O}/M_{H_2O}} = 2\, B' \, m_{NaCl}\\ \end{split} \label{eq:DT_salt} \end{equation*}

(5.45)

Typically colligative properties are not so significant for solutions of polymers due to the low density of polymers (i.e. low number of molecules), the lack of dissociation, and the large molar masses ($\Delta T \propto 1/M$).
So obviously the colligative properties can be used to determine $M$ of the solute (via $x_B$).
Usually the cryoscopic constants (for the freezing point depression which thus have absolute negative values) are larger than the ebullioscopic constants (for the boiling point elevation).