Efficiency and Carnot cycle

3.6 Efficiency and Carnot cycle

The efficiency \(\eta\) of a heat engine is defined as

\begin{equation*} \eta = |\mbox{work performed}| / \mbox{(heat input)} = |w| / q_1 \label{eq:def_efficiency} \end{equation*}

(3.7)

Figure 3.3: Illustration of the efficiency of a reversible cycle process (heat engine) operating between two temperatures. According to Eq. (3.7) we find \(\eta = 5 / 20 = 25\%\).

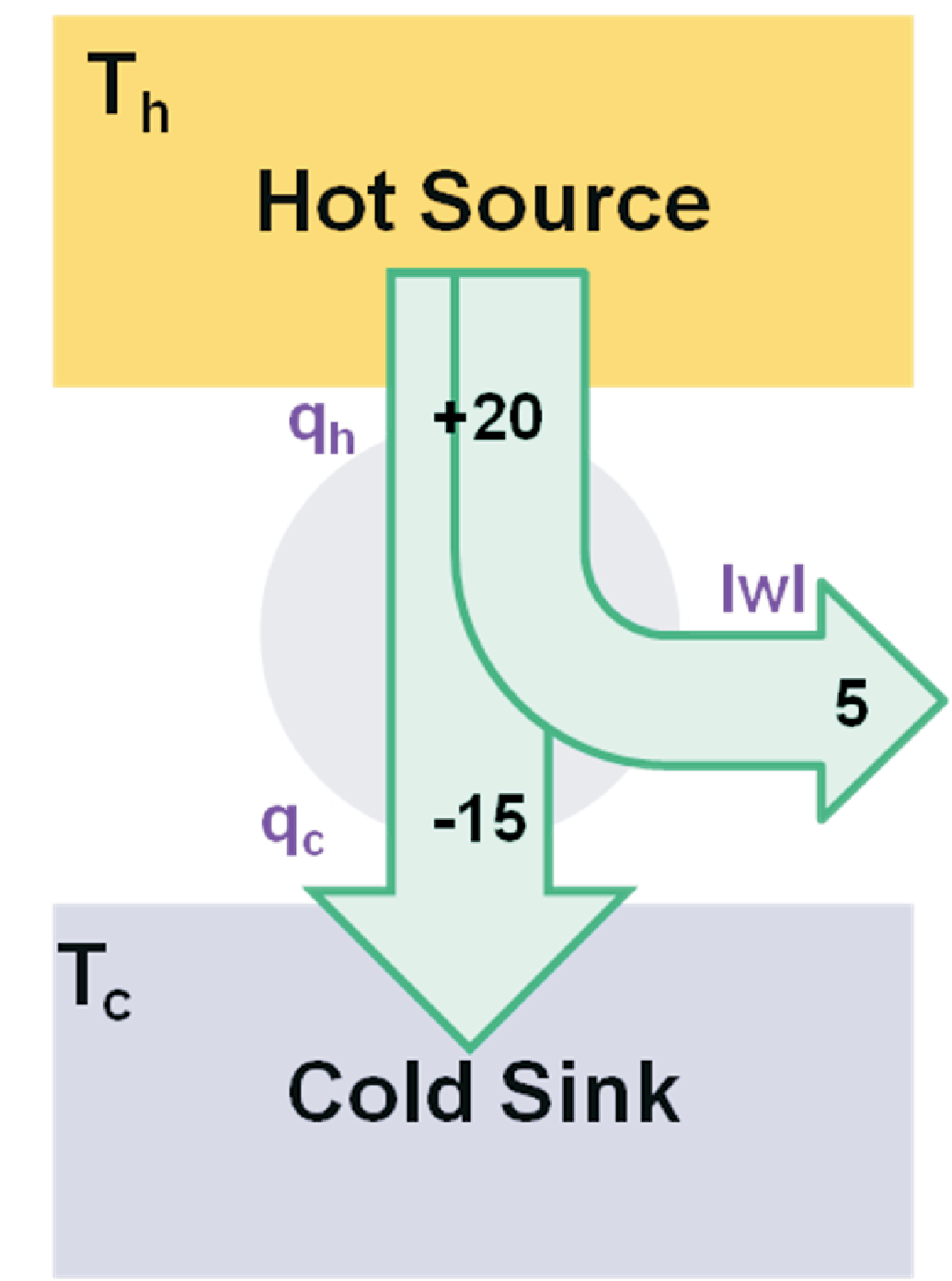
We now combine the first and second law to calculate the efficiency for any reversible cycle process taking heat \(q_1\) from a hot source at \(T_1\), releasing some heat \(q_2\) to a cold sink at \(T_2\) and performing work \(w\) . This scheme is illustrated in Fig. 3.3; soon we will discuss the Carnot cycle as the most important candidate for such a process. But before we will check the efficiency resulting from the first and second law. According to the first law which just reflects energy conservation we find \(w= q_1 + q_2\) where \(q_1 \gt 0\), \(q_2 \lt 0\), and thus \(w \gt 0\). According to the second law the entropy \(S\) is a state function for which after one cycle we find \(0 = \Delta S = q_1/T_1 + q_2/T_2\). Including these results into the definition for the efficiency we get

\begin{equation*} \eta =\frac{w}{q_1} = \frac{q_1+q_2}{q_1}= 1 + \frac{q_2}{q_1} = 1 - \frac{T_2}{T_1} = \frac{T_1 - T_2}{T_1} \label{eq:solution_efficiency} \end{equation*}

(3.8)

So obviously the entropy is intrinsically related to efficiency. Eq. (3.8) directly implies two remarkable results:

Obviously, all reversible engines operating at the same temperatures have the same efficiency.
Obviously, no cyclic process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work.

These two statements can easily (obviously) be extracted from the first and second law of thermodynamics, but actually statement 2 (postulated by Kelvin) and statement 1 (concluded by Carnot) have been the historical starting points for finding the second law.

Figure 3.4: Perpetual motion machine of 2. kind.

In what follows we will briefly repeat the reasoning and it becomes obvious what a big challenge it was (and is) to extract the existence of a state function ”entropy” from the statement of Kelvin. To make sure: Nothing we have learned in this chapter we now can take for granted. Just the statement 2 above we will use as a starting point (as an additional knowledge to the energy conservation as stated in the first law).
First we now check for the combination of cycle processes shown in Fig. 3.4. Since we are discussing reversible processes we can invert the direction of flow in the second cycle, i.e. we discuss a refrigerator (or heat pump) taking heat from the cold ”sink” and transporting it to the hot ”source” by applying work.
Let us now assume that process A has a larger efficiency than process B (the contradiction to statement 1). Of course we now can tune the two processes that process A exactly releases as much heat into the sink as process B extracts from the sink. As net effect we could perform work just by cooling the hot source. BUT this is in contradiction to (Kelvin’s) statement 2. So all reversible cycle processes acting between two heat reservoirs must have the same efficiency which proves statement 1.
We now can calculate the efficiency for any reversible cycle process to find the general result, and this will of course be the Carnot cycle. With respect to work and heat we find the following quantitative results:

A \(\rightarrow\) B: \(\Delta U = 0\), \(w_1 = - q_1 = - n\,R\,T_1 \ln \frac{V_2}{V_1}\)
B \(\rightarrow\) C: \(q = 0\), \(\Delta U = w_2 = n\,C_V \left( T_2 - T_1 \right)\)
C \(\rightarrow\) D: \(\Delta U = 0\), \(w_3 = - q_2 = - n\,R\,T_2 \ln \frac{V_4}{V_3} = n\,R\,T_2 \ln \frac{V_3}{V_4}\)
D \(\rightarrow\) A: \(q = 0\), \(\Delta U = w_4 = n\,C_V \left( T_1 - T_2 \right) = - w_2 \, (\)B\(\rightarrow\)C)

Figure 3.5: A general cycle process being divided into Carnot cycles.

Additionally we find from the Poisson equations (2.35)

\begin{equation*} T_1 V_1^{\gamma-1} = T_2 V_4^{\gamma-1} \quad \mbox{and} \quad T_1 V_2^{\gamma-1} = T_2 V_3^{\gamma-1} \quad \Rightarrow \quad \frac{V_2}{V_1} = \frac{V_3}{V_4} \label{eq:v_ratio_efficiency} \end{equation*}

(3.9)

Inserting this result into the definition for the efficiency we find

\begin{equation*} \eta = \frac{q_1 + q_2}{q_1}= \frac{T_1 \ln (V_2/V_1) - T_2 \ln (V_3/V_4)}{T_1 \ln (V_2/V_1)} = \frac{T_1 - T_2}{T_1} \label{eq:efficiency_T_eq} \end{equation*}

(3.10)

Rearranging Eq. (3.10) we find

\begin{equation*} \frac{q_1 + q_2}{q_1}= \frac{T_1 - T_2}{T_1} \quad \Rightarrow \quad 1 + \frac{q_2}{q_1}= 1 - \frac{T_2}{T_1} \quad \Rightarrow \quad \frac{q_1}{T_1}+\frac{q_2}{T_2} = 0 \label{eq:input_def_entropy} \end{equation*}

(3.11)

which proves the entropy to be a state function at least for a all reversible cycle processes acting between two heat reservoirs. To generalize for all reversible cycle processes we use Fig. 3.5:
Any process can be divided into Carnot cycles. Inside its \(p - V\) contour the counter-rotating processes cancel out. Around the perimeter no counter-rotating processes exist, so all outermost parts of the Carnot cycles add up (with respect to energy and with respect to entropy). Taking now the limit for infinitesimally small cycles any shape can be represented perfectly by Carnot cycles leading to

\begin{equation*} 0 = \lim_{i \rightarrow \infty} \sum_i \frac{q_i}{T_i}= \oint \frac{dq}{T} = \oint dS \label{eq:S_state_function} \end{equation*}

(3.12)

for all reversible cycle processes. That irreversible processes are less efficient we already found in section 2.6. This clarifies the inequality sign in Eq. (3.1).
In summary, we proved that the 2 above statements and ”entropy is a state function” are equivalent; however the introduction of entropy allows the most easiest quantitative evaluation of thermodynamic properties. In addition, the equation

\begin{equation*} \frac{q_1 + q_2}{q_1}= \frac{T_1 - T_2}{T_1} \label{eq:TD_T_scale} \end{equation*}

(3.13)

motivated Kelvin to suggest a new thermodynamic \(T\)-scale, just depending on efficiency measurements.
Typical values for \(\eta\) are between 0.3 to 0.4. \(\eta = 1\) is not possible, because the cold bath is always heated! (As we will see later \(T = 0\) K cannot be reached).
Fig. 3.6 shows the Otto engine as an example of a highly relevant cycle process which is not the Carnot process.

Figure 3.6: Otto engine: Cycle of isentropic and isochoric processes.

It consists of

1-2: Isentropic compression \(p_2\,V_2^{\gamma}=p_1\,V_1^{\gamma}\) with \(\gamma = C_p / C_V = 7 / 5 = 1.4\) (O\(_2\) or N\(_2\) has 3 translational plus 2 rotational dof).
2-3: Isochoric increase of \(p\) by heating.
3-4: Isentropic expansion.
4-1: Isochoric decrease of \(p\) by cooling.

In reality the edges marked by the circles in Fig. 3.6 will not be fully isochoric due to piston (German: Kolben) movement and leaky valves. The piston serves for the changes in volume. The combustion of the fuel takes some time, thus, the piston moves during the combustion. By the movement, the volume is changed, thus, the process is not fully isochoric.