Adiabatic changes - Poisson equations

2.11 Adiabatic changes - Poisson equations

The next sections will discuss the theoretical background for describing experiments performed under various specific boundary conditions. These boundary conditions are often a significant simplification for the real experimental boundary conditions but provide the necessary simplification to model very general aspects related to that type of boundary condition. In this section we discuss adiabatic processes, i.e. processes without heat transfer to or from the surrounding. Such a condition can of course be realized by good thermal insulation or is found for fast processes for which the reaction time is so small that no reasonable amount of heat can be exchanged with the surrounding. Explosions are a typical example for such reactions. Propagation of sound and combustion engines are other (technically highly relevant) examples; e.g. during adiabatic expansion work is done by the ideal system only on the expense of its internal energy. The internal energy of a perfect gas is \(dU = n\,C_V\,dT\) (it depends on temperature only), thus for an adiabatic expansion, \(dT\) must be smaller zero (i.e. cooling takes place). For a complete description we apply the first law:

\begin{equation*} dU = \delta q + \delta w = 0 + \delta w = C_V dT \quad \Rightarrow \quad C_V dT = -p dV \label{eq:adiab_1} \end{equation*}

(2.31)

Applying this equation to adiabatic reversible processes of perfect gases we find:

\begin{equation*} \frac{C_V \,dT}{T} = - \frac{n\,R\,dV}{V} \quad \Rightarrow \quad C_V\int_{T_1}^{T_2} \frac{dT}{T} = - n\,R \int_{V_1}^{V_2} \frac{dV}{V} \quad \Rightarrow \quad \left(\frac{T_2}{T_1} \right)^{\frac{C_V}{n\,R}} = \left(\frac{V_1}{V_2} \right) \label{eq:adiab_2} \end{equation*}

(2.32)

\begin{equation*} \left(\frac{T_2}{T_1} \right) = \left(\frac{V_1}{V_2} \right)^{\frac{n\,R}{C_V}} \quad \mbox{with} \quad \frac{n\,R}{C_V} = \frac{R}{C_{V,m}} = \frac{C_{p,m}-C_{V,m}}{C_{V,m}}=\gamma - 1 \label{eq:adiab_3} \end{equation*}

(2.33)

Here we have introduced the adiabatic exponent \(\gamma = \frac{C_{p,m}}{C_{V,m}}\). Eq. (2.33) can be rearranged

\begin{equation*} T_1 \, V_1^{\gamma-1} = T_2 \, V_2^{\gamma-1} \quad \mbox{i.e.}\quad T \, V^{\gamma-1} = const. \quad \mbox{for adiabatic processes.} \label{eq:adiab_4} \end{equation*}

(2.34)

Using \(T = \frac{p\,V_m}{R}\), resp. \(V_m = \frac{R\,T}{p}\) we get the set of Poisson equations

\begin{equation*} \begin{split} T\,V^{\gamma -1} & = const.\\ p\,V^{\gamma} & = const.\\ T^\gamma\,p^{1-\gamma} & = const.\\ \end{split} \label{eq:Poisson} \end{equation*}

(2.35)

Figure 2.8: Illustration of the differences between adiabatic and isothermal expansion. a) \(p\,V\,T\) diagram, still the adiabate is on the surface of the allowed states for a perfect gas; b) \(p\,V\) diagram.

For the slopes we find

\begin{equation*} \begin{split} p\,V = const.: & \left(\frac{\partial p}{\partial V}\right)_T = \frac{-n\,R\,T}{V^2} = \frac{-p\,V}{V^2} = \frac{-p}{V}\\ p\,V^{\gamma}= const.: & \left(\frac{\partial p}{\partial V}\right)_{\delta q = 0} = \frac{-\gamma\, const.}{V^{\gamma+1}} = \frac{-\gamma\,p\,V^{\gamma}}{V^{\gamma+1}} = \frac{-p}{V} \gamma\\ \end{split} \label{eq:pV_slopes} \end{equation*}

(2.36)

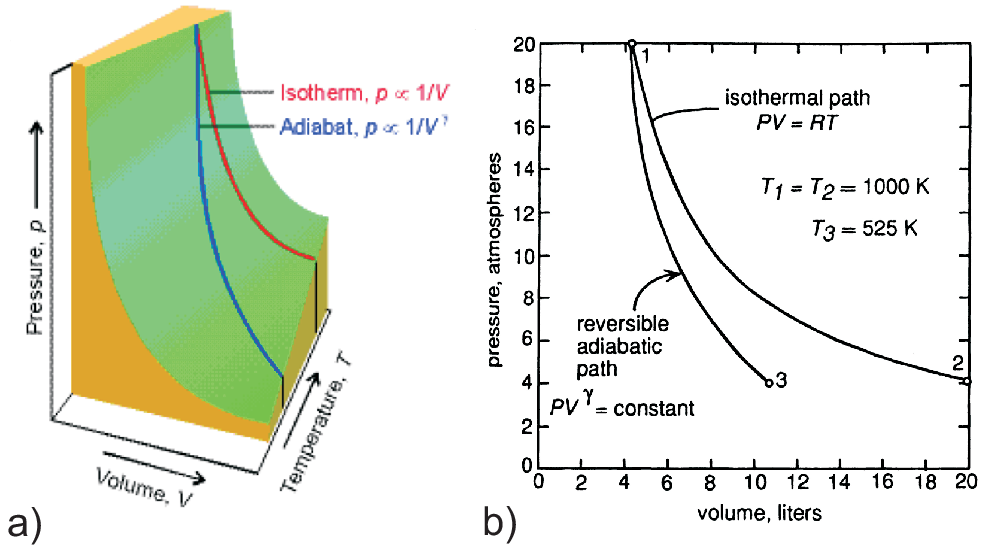
Since \(\gamma \gt 1\) the adiabate shows a steeper slope than the isotherm (cf. Fig. 2.8).
\(\gamma\) depends on molecular nature of the perfect gas:
- Monatomic perfect gas, \(\gamma = 5/3\)
- Diatomic perfect gas, \(\gamma = 7/5\) (neglecting oscillations)
- In general: \(\gamma = (dof + 2) / dof\) (\(dof\) = degree of freedom)
Consequences:
- The adiabate is more steep compared to the isotherm. Thus intersections of isothermal and adiabatic curves will exist.
- Therefore \(w \neq 0\) in a cyclic process based on adiabatic and isothermal changes.