3.5 Carnot cycle: p-V diagram and T-S diagram

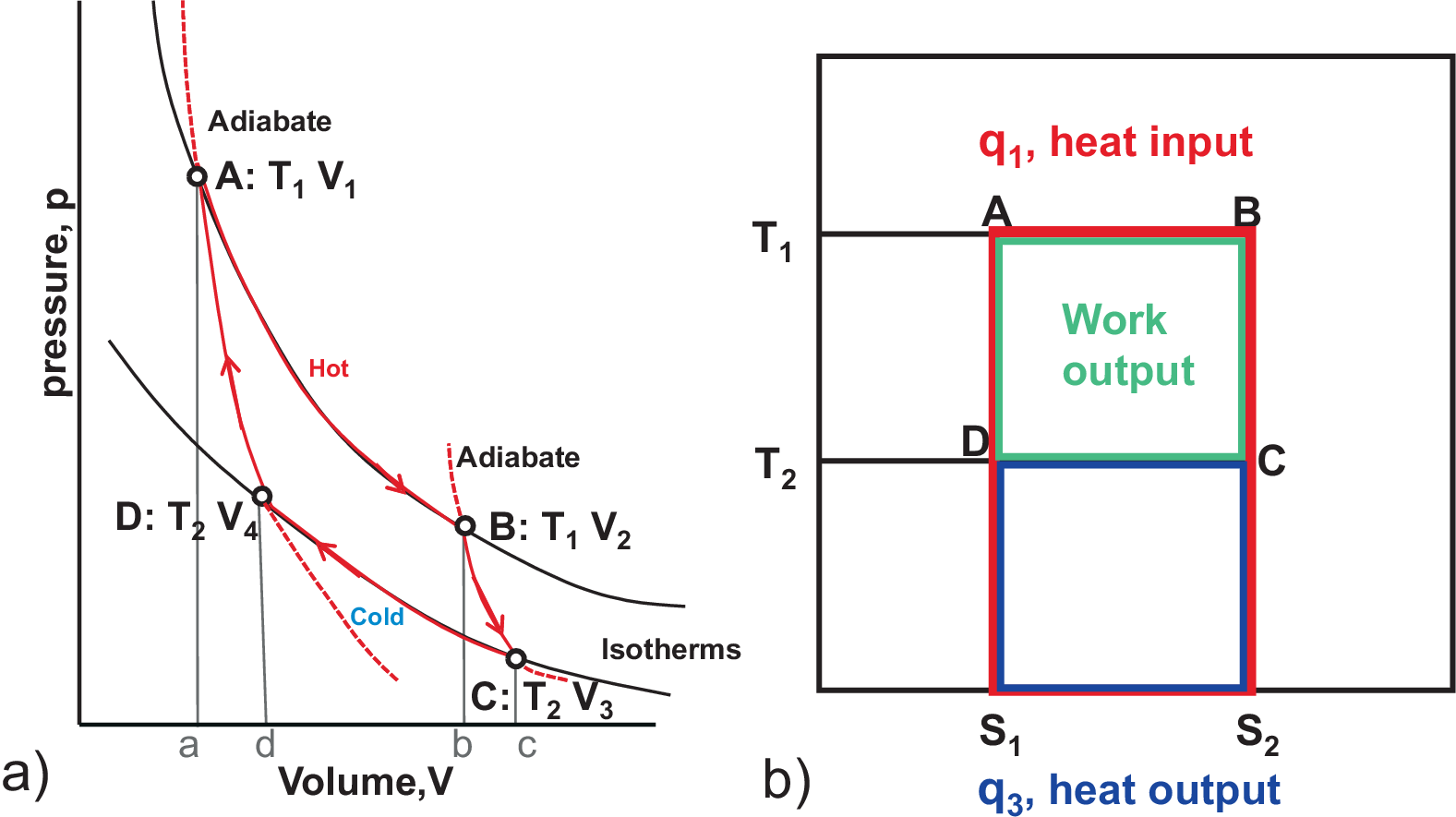
In what follows we discuss one of the most important concepts of thermodynamics, the Carnot cycle. In general in a circular process the thermodynamic system passes several exchange points until it ends up in its starting point. It is important to note that for different branches the surrounding can change, i.e. energy in terms of heat or work can be transferred from different heat reservoirs. Fig. 3.2 a) illustrates a Carnot cycle. This is a combination of reversible isothermal and adiabatic expansion and compression of a perfect gas:

• A \(\rightarrow\) B: \(q_1\) is isothermally (@\(T_1\)) transferred from the first heat reservoir to the system (\(w_1\) = area ABba)

• B \(\rightarrow\) C: adiabatic expansion reducing the temperature from \(T_1\) to \(T_2\) (\(w_2\) = area BCcb)

• C \(\rightarrow\) D: \(q_2\) is isothermally (@\(T_2\)) transferred from the system to the second heat reservoir (\(w_3\) = area DCcd)

• D \(\rightarrow\) A: adiabatic compression, increasing temperature from \(T_2\) to \(T_1\) (\(w_4\) = area ADda)

The gas becomes cold and hot after adiabatic expansion and compression, respectively. The area in the \(p - V\) diagram represents expansion work \(w\). Now we discuss the \(T - S\) diagram of a Carnot cycle as shown in Fig. 3.2 b). Since \(T\,dS = \delta q_{rev}\) the area in the \(T - S\) diagram represents \(q_{rev}\). So no contribution to \(q_{rev}\) comes from the adiabatic processes. For the isothermal processes we have \(w = -q\), so the work done (output) is given by the area ABCD.

• A \(\rightarrow\) B: heat input (\(-q_1 = w_1 =\) area ABS\(_2\)S\(_1\))

• B \(\rightarrow\) C: \(q = 0\)

• C \(\rightarrow\) D: heat output (\(-q_3 = w_3 =\) area CS\(_2\)S\(_1\)D)

• D \(\rightarrow\) A: \(q = 0\)

Obviously larger \(T\)-differences and large \(S\)-differences are needed for efficient processes (i.e. more work can be performed). The \(w\)-contributions from the adiabatic steps are canceling out. Thus only the isothermal steps contribute to heat and by that to work.

© J. Carstensen (TD Kin I)