Calculation of μ for different models

2.14 Calculation of $\mu$ for different models

For virial coefficients as well as for the vdW-equation we will prove some quite fundamental results related to the Joule-Thomson coefficient $\mu$. The following equation already needs results from the second law of thermodynamics, i.e. the entropy $S$ is used as well as a Maxwell relation between mixed partial derivatives. So you may take this section as a motivation for discussing the second law, because obviously not all problems can be solved just by conservation of energy.

\begin{equation*} \begin{split} \mu \;=&\quad \left(\frac{\partial T}{\partial p} \right)_H = - \frac{\left(\frac{\partial H}{\partial p} \right)_T}{\left(\frac{\partial H}{\partial T} \right)_p} \stackrel{1}=\frac{T\,\left(\frac{\partial V}{\partial T} \right)_p-V}{C_p}\stackrel{2}=\frac{V}{C_p}\left(\alpha T - 1 \right)\\ 1\;: \;& \quad - \left(\frac{\partial H}{\partial p} \right)_T = \left(\frac{\partial}{\partial p} \right)_T \left(-T\,dS-V\,dp \right) = - T \left(\frac{\partial S}{\partial p} \right)_T - V = T\, \left(\frac{\partial V}{\partial T} \right)_p -V\\ 2\;:\; & \quad \alpha = \frac{1}{V} \left(\frac{\partial V}{\partial T} \right)_p \quad \mbox{$\alpha$: expansion coefficient.}\\ \end{split} \label{eq:mu_Joule-Thomson} \end{equation*}

(2.42)

The expansion coefficient we discussed before in Eq. (2.6). Applying the above equation to different thermal equations of state we find

Ideal gas

\begin{equation*} \mu_{ideal} = \frac{T\,\left(\frac{\partial V}{\partial T} \right)_p-V}{C_p} = \frac{1}{C_p}\left(\frac{n\,R\,T}{p} -V \right) = 0 \label{eq:mu_ideal} \end{equation*}

(2.43)

Virial approach according to the Berlin form (cf. Eq. (1.10)): $V = R\,T/p + B$

\begin{equation*} \mu_{virial}(T) = \frac{T\,\left(\frac{\partial V}{\partial T} \right)_p-V}{C_p} = \frac{T\left(\frac{R}{p} + \left(\frac{\partial B}{\partial T} \right)_p\right)-\left(\frac{R\,T}{p}+B\right)}{C_p} = \frac{T\left(\frac{\partial B}{\partial T}\right)_p-B}{C_p} \label{eq:mu_virial} \end{equation*}

(2.44)

At the Boyle temperature $T_B$ the virial coefficient $B$ is zero (the gas behaves much like a perfect gas), thus $\mu(T \rightarrow T_B) = 0$.

vdW approach with $B = b - a / (RT)$ (cf. Eq. (1.25))

\begin{equation*} \mu_{vdW} = \frac{T\left(\frac{\partial B}{\partial T}\right)_p-B}{C_p} = \frac{\frac{2\,a}{RT}-b}{C_p} \quad \Rightarrow \quad T_i = \frac{2\,a}{R\,b} \label{eq:mu_vdW} \end{equation*}

(2.45)

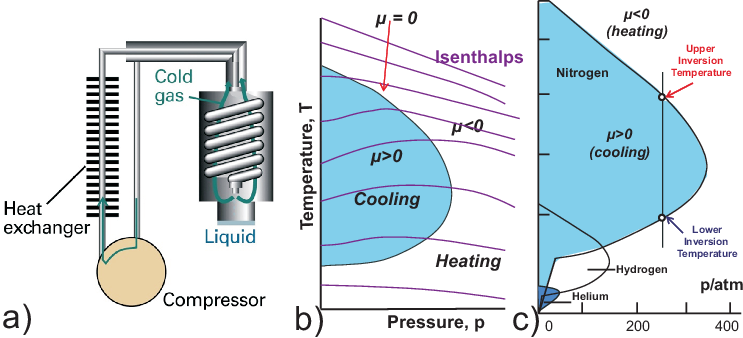
with $T_i$: inversion temperature where $\mu$ changes sign.

The Joule-Thomson effect is highly relevant for cooling. Fig. 2.10 shows the Linde process for production of liquid air: The gas must be beneath its inversion temperature (examples for upper inversion temperatures: He: 35 K, H$_2$: 224 K, N$_2$: 866 K). The gas cooled by expansion cools compressed gas, further expansion could lead to liquid.

Figure 2.10: a) scheme of Linde process; b) $pT$ diagram showing the regimes separated by $\mu = 0$; c) cooling regime for several gases.

2.14 Calculation of \(\mu\) for different models