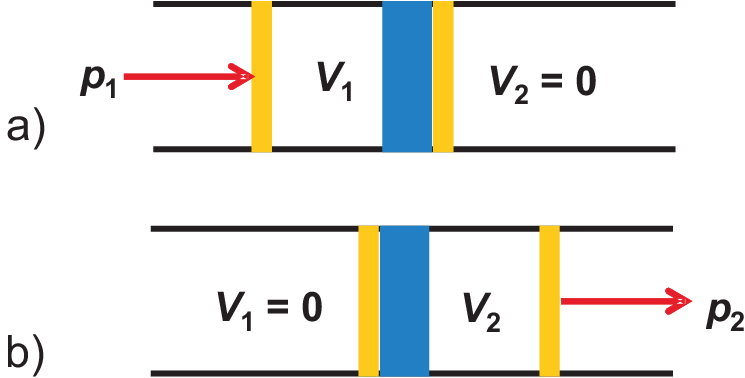
Figure 2.9:
Illustration of isenthalpic expansion: a) at beginning of experiment, b) after finishing the
experiment.
Performing an experiment as illustrated in Fig. 2.9, one typically observes a temperature change when pressing gas through a throttle.

Gas becomes cold / warm during expansion by counteracting attractive / repulsive forces, thus reducing / increasing \(U\).
Sign of \(\Delta T\) depends on the Joule-Thomson coefficient which depends on \(p\) and \(T\). Being adiabatic, we find
|
| \begin{equation*} \Delta U = \Delta q + \Delta w = \Delta w \label{eq:DU_Joule-Thomson} \end{equation*} | (2.38) |
According to Fig. 2.9 a) we find for system 1 (left of diaphragm)
|
| \begin{equation*} \Delta U_1 = 0 - U_1=-U_1=- p_1\, (0-V_1) = p_1\,V_1 \label{eq:DU1_Joule-Thomson} \end{equation*} | (2.39) |
According to Fig. 2.9 b) we find for system 2 (right of diaphragm)
|
| \begin{equation*} \Delta U_2 = U_2 - 0= U_2=- p_2\, (V_2-0) = - p_2\,V_2 \label{eq:DU2_Joule-Thomson} \end{equation*} | (2.40) |
© J. Carstensen (TD Kin I)