Virial coefficients: empirical approx. of the compression factor

1.7 Virial coefficients: empirical approx. of the compression factor

Often in science experimental data has to be approximated, and most often this is done by a series expansion into polynoms. This is not done because the whole nature can nicely be described by polynoms; it is just done because polynom expansions are mathematically so easy: to increase the accuracy of the approximation you just increase the order of the polynom (and besides polynom coefficients are linear coefficients which are most easy to fit). The virial coefficients are just these coefficients to approximate measured compression factors \(Z\). Two standard expansions (Leiden and Berlin form) are used depending on \(p\) or \(1/V_m\) being varied in the measurement of \(Z\) (for \(p \rightarrow 0\) as well as for \(1/V_m \rightarrow 0\) the perfect gas is expected):

\begin{equation*} \begin{split} Z & = \; \; \; 1 + \text{correction terms}\\ Z & = \left(1 + \frac{B}{V_m} + \frac{C}{V_m^2} + \cdots \right) \quad \Rightarrow \quad p\,V_m = RT \left(1 + \frac{B}{V_m} + \frac{C}{V_m^2} + \cdots \right) \quad \text{Leiden}\\ Z & = \,\left(1 + B' p + C' p^2 + \cdots \right) \quad \Rightarrow \quad p\,V_m = RT \left(1 + B' p + C' p^2 + \cdots \right) \quad \text{Berlin} \end{split} \label{eq:Leiden_Berlin} \end{equation*}

(1.10)

Figure 1.3: Compression factor vs. \(p\) for several temperatures

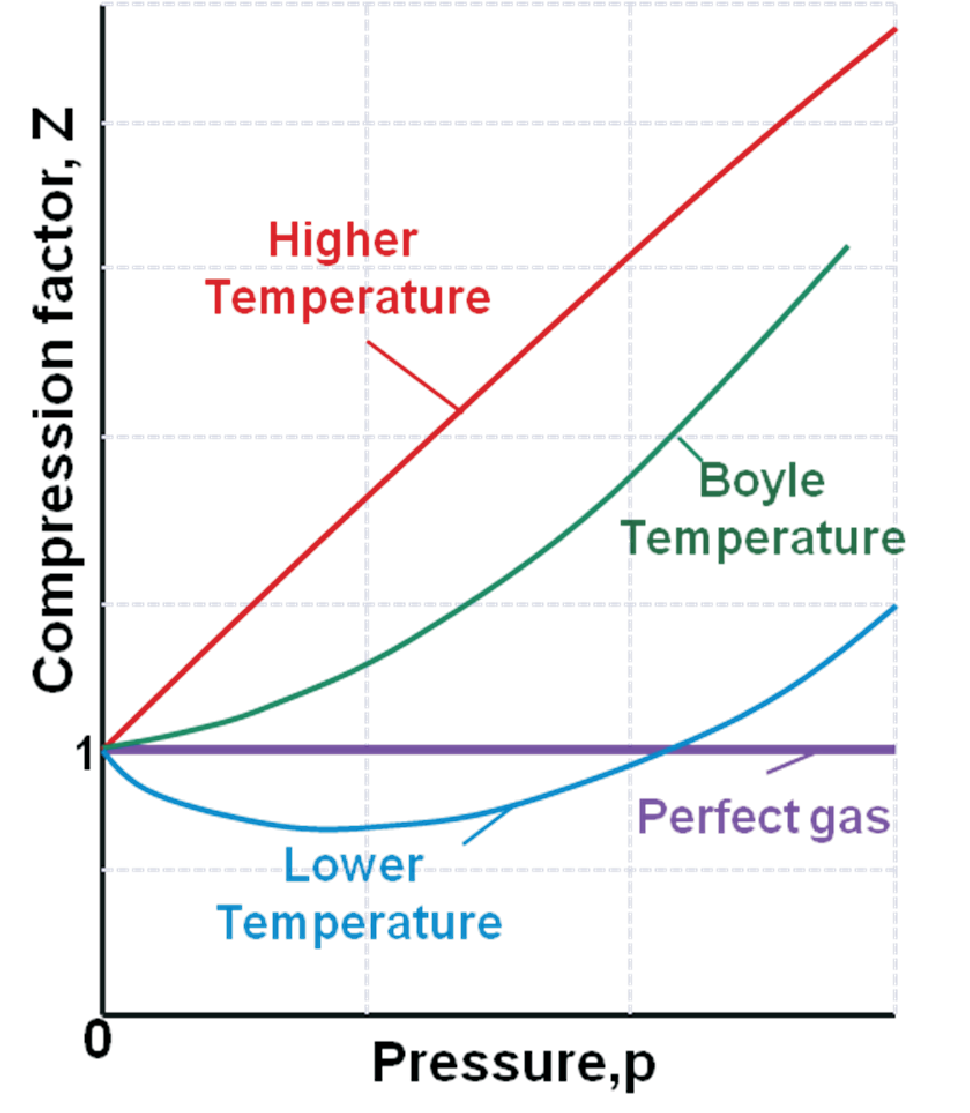
The zeroth order just represents the perfect gas. Theoretically an infinite number of terms can be added to this state function to improve the approximation of measured \(Z\) data. Practically only the additional \(B\) and \(C\) terms are important. Despite some integer numbers the Berlin form just represents the Taylor expansion of \(Z(p)\) at \(p \rightarrow 0\). So the parameters \(B'\) and \(C'\) are most easily calculated from the derivatives of \(Z(p)\) to corresponding order. As shown in Fig. 1.3 \(Z(p)\) and thus the virial coefficients depend on temperature. Although for all temperatures \(\lim_{p \rightarrow 0} Z(p) \rightarrow 1\) (\(\lim_{V_m \rightarrow \infty} Z(V_m) \rightarrow 1\)) even for \(p\rightarrow 0\) (\(V_m \rightarrow \infty\)) the properties of real gases are not identical to those of a perfect gas since they depend on higher order effects as well. Now we define the Boyle temperature \(T_B\) at which the properties of real gases most strongly reflect the properties of a perfect gas. At \(T_B\) the slope \(Z(p)\) vanishes for \(p\rightarrow 0\), i.e.

\begin{equation*} \left(\frac{\partial Z}{\partial p}\right)_{p\rightarrow 0, T = T_B} = 0 \end{equation*}

(1.11)

In summary the virial approach is limited to low and moderate pressures (since it is a Taylor expansion around \(p = 0\)). It allows to model the \(T\)-dependence of intermolecular forces via the \(T\)-dependence of \(B'(T)\) (being smaller or larger zero). It allows to understand the deviations from a perfect gas at low \(p\). At Boyle temperature \(T_B\) real gases behave best like perfect gases, i.e. the longest range can be found with \(p\,V_m = R \, T_B\). At Boyle temperature and at low pressure attractive and repulsive forces compensate each other, so typically low attractive forces imply low Boyle temperatures, e.g. \(T_B(\)He\() = 22.64\) K but \(T_B(\)Air\() = 346.8\) K. The biggest drawback of the virial approach is that the physical meaning of the \(B, C\) parameters remains unclear.