Description of real gases: Compression factor

1.6 Description of real gases: Compression factor

The compression factor \(Z\) describes the deviation from perfect gases. It is defined as

\begin{equation*} Z = \frac{p\,V_m}{RT} = \frac{p\,V_m}{p\,V_m^0} = \frac{V_m}{V_m^0} \quad \mbox{, i.e.} \quad Z \gt 1 \quad \Rightarrow \quad V_m \gt V_m^0 \end{equation*}

(1.9)

Here \(V_m^0\) is the molar volume of a perfect gas and \(V_m\) the measured volume of the real gas. Any deviation from \(Z = 1\) indicates a non-ideality and quite obviously the compression factor \(Z\) is an indicator for intermolecular forces:

For attractive forces the real gas occupies less space compared to the perfect gas, i.e. \(Z \lt 1\).
For repulsive forces the real gas occupies more space compared to the perfect gas, i.e. \(Z \gt 1\).
For \(p \rightarrow 0\): approximation of the perfect gas, thus \(Z \rightarrow 1\).
Generally an increase of \(Z\) with increasing \(p\) (increasing repulsive forces) can be expected.
Compression factors can be theoretically predicted from the Lennard-Jones potential: potential energy \(U(r)\) of two molecules vs. their separation \(r\): \(U = C_1 / r^{12} - C_2 / r^6\).

Figure 1.2: Compression factor vs. \(p\) for several gases/fluids

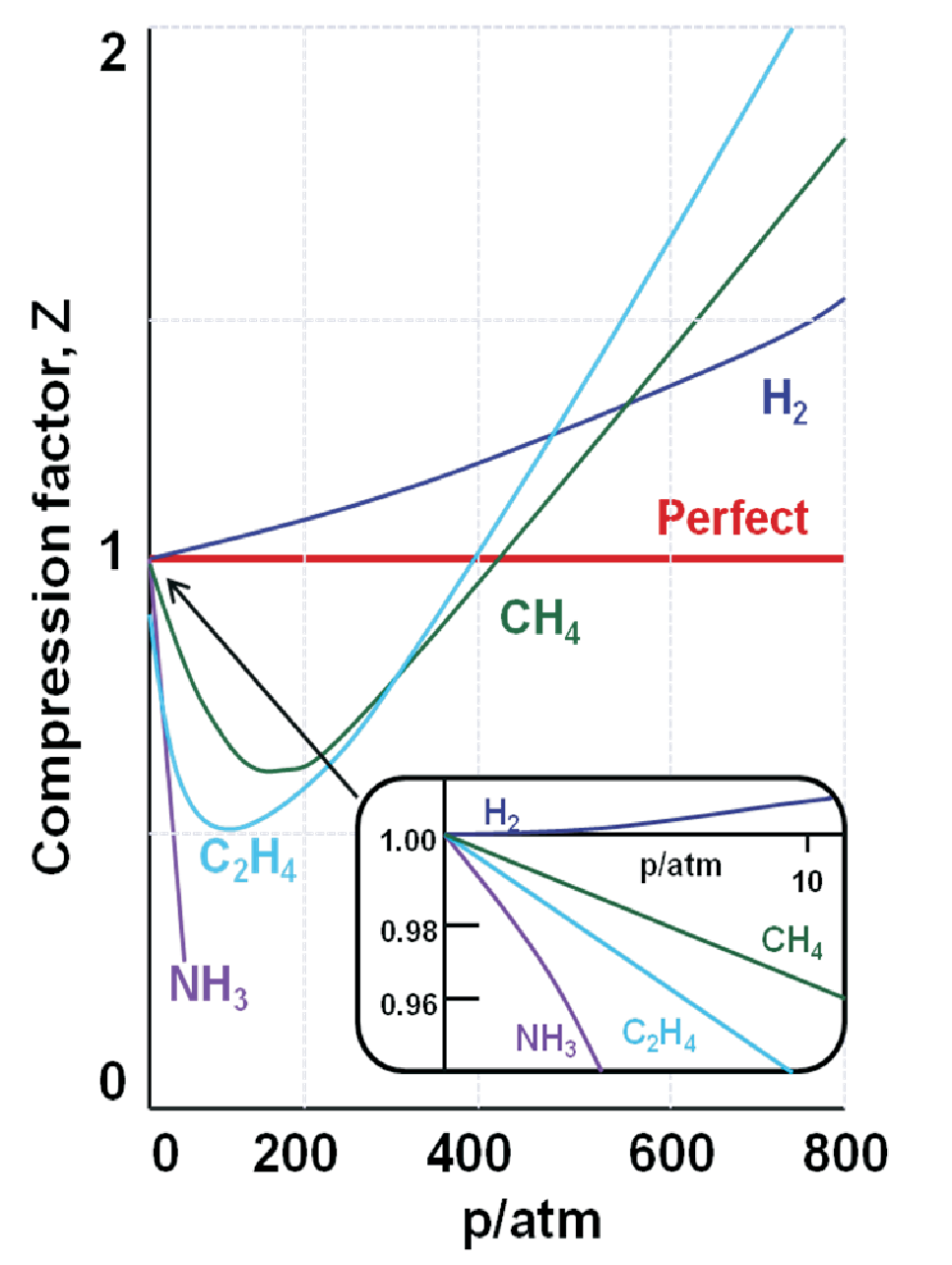
Fig. 1.2 shows examples for compression factors of several materials. Actually these are not only gases. Gases and liquids have much in common, this is e.g. demonstrated by the presence of a supercritical fluid where the separation into gas and liquid state vanishes. As we will see from the discussion of van-der-Waals gases attractive forces between gas molecules can lead to the formation of fluids. An indication for this is \(Z\) being smaller 1 for low pressures, holding in the figure e.g. for ammonia (NH\(_3\)). Much like in water the hydrogen bonding between NH\(_3\) molecules induces the necessary attractive forces. In contrast H\(_2\) has no attractive contribution but only the repulsive ones due to the repulsion of the binding electrons, thus \(Z\) is always larger 1. All gases shown in Fig. 1.2 contain a small number of atoms, thus can be represented by hard spheres (in contrast e.g. to long organic molecules leading to additional effects). The common features of gases being described by hard spheres potentials are:

At low separation (correlating with high pressure), repulsive forces are dominant.
Repulsive and attractive forces are balanced at the minimum of the potential curve (roughly bonding distance in a molecule).
At larger separation the low pressure scenario of the perfect gas is approximated.