Here we will state some very important and famous results related to heat capacity.
Usually \(C\) is positive; famous exceptions are:
Metastable systems, e.g. clusters (energy dominated by surface).
Black holes. The absorption of mass increases its internal energy \(U\), but the temperature \(T\) of a black hole is inversely proportional to its mass. Thus: the more mass a black hole absorbs, the colder it becomes, i.e. \(C_V= \Delta U / \Delta T \lt 0\).
Dulong and Petit (1819): \(C_{p,m}(solid) = 3 R = 24.9\) J/K.
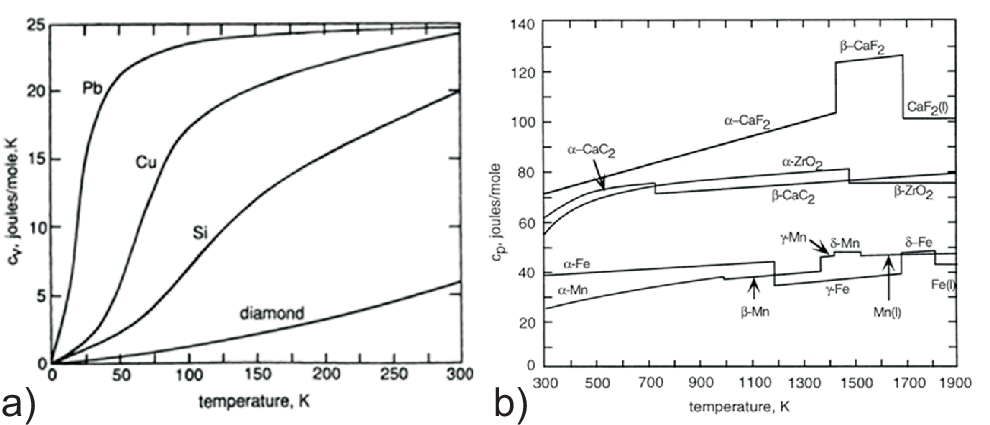
This is a good approximation for the metallic elements at high \(T\) (room temperature): \(C\) ranges from about 2.8 \(R\) to 3.4 \(R\) (cf. the extrapolation for large \(T\) in Figs. 2.5 a) and 2.6).
It can be explained by the excitation of 3\(N\) oscillations, every oscillation mode contributes with \(R\).
Strong deviations are found at low \(T\); in this regime the \(T^3\)-law of Debye holds, or the linear \(T\)-dependence (electrons in metals) is found (cf. Fig. 2.6).
Jumps in \(C_p/T\) at phase transitions show up (cf. Fig. 2.5 b)).
Smaller heat capacities are found for solids of light, tightly-bonded atoms such as beryllium (2.0 \(R\)) and diamond at only 0.735 \(R\) (cf. Fig. 2.5 a). The latter conditions create large quantum vibrational energy spacing, so that many vibrational modes are frozen out still at room temperature.
Kopp (1865):
\(C_p\) of a solid/liquid is the sum of the atomic heat capacities of the elements composing it.
Elements having lower heat capacities (as expected by the Dulong and Petit law) retain these lower values even in their compounds
e.g. KCl: \(C_{V,m} \approx 6 R\), MgCl\(_2\): \(C_{V,m} \approx 9 R\).
Extension to slurries/solutions possible (composition average), e.g.
|
| \begin{equation*} C_{p,m}(solution) = x_{water} C_{p,m}(water) + x_{salt} C_{p,m}(salt) \quad \mbox{where $x$ is the corresponding mole fraction} \label{eq:Cpm_solution} \end{equation*} | (2.24) |

© J. Carstensen (TD Kin I)