Estimation of heat capacity for gases

2.9.2 Estimation of heat capacity for gases

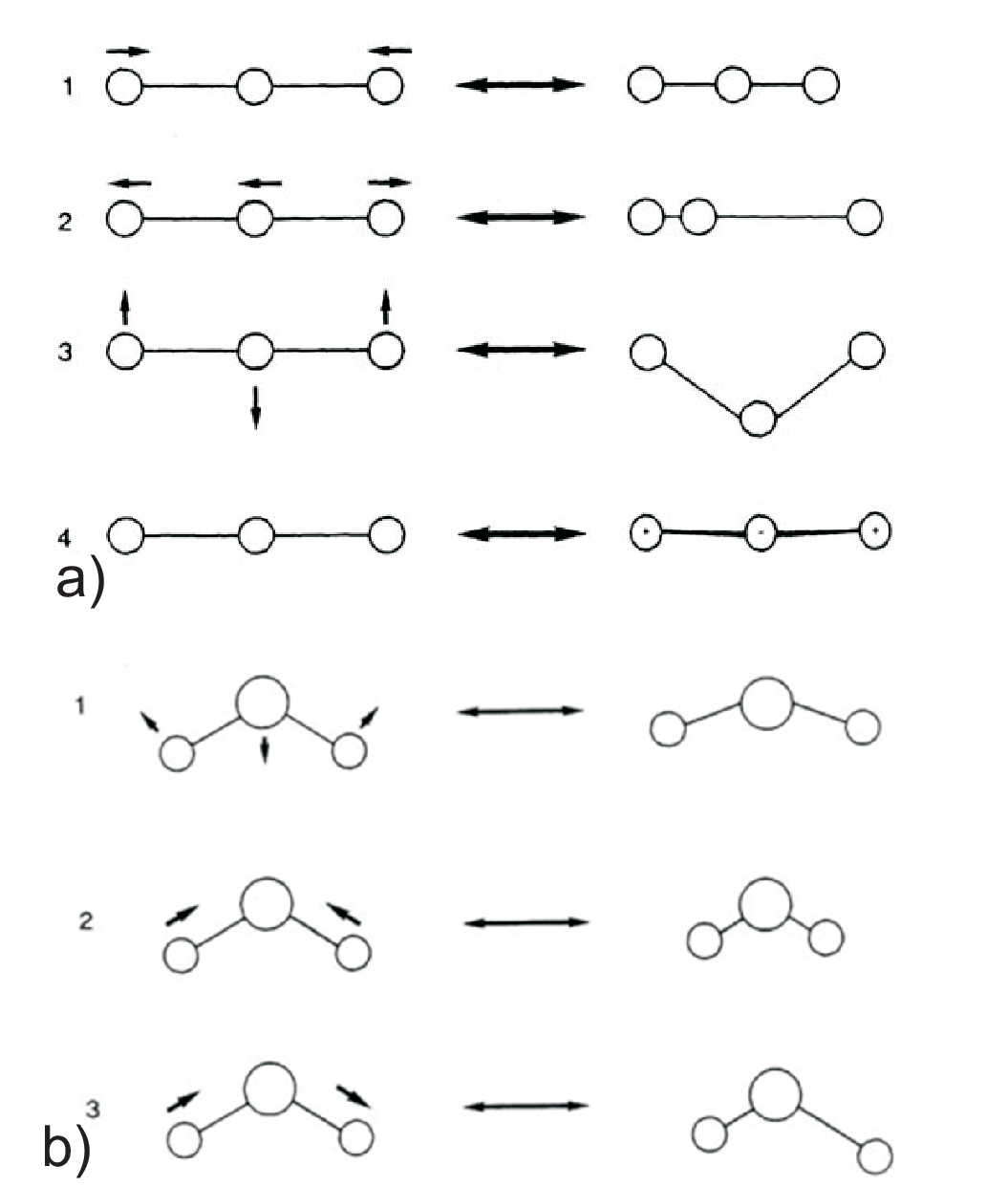
The heat capacity of gases depends on the structure of the molecules since this defines the distribution of the ”degrees of freedom” (dof) in the modes of motion (translation, rotation, oscillation). Degrees of freedom are defined as the number of parameters necessary to specify the position of each atom of the molecule.

Figure 2.7: Oscillation modes of a three-atomic molecule: a) linear, b) angular.

\(N\) is the number of atoms \(\Rightarrow\) dof = 3 \(N\) (position of each atom in 3D space).
Translation of the (whole) molecule \(\Rightarrow\) dof = 3 per molecule, for one mole each contributing with \((1/2) R\).
Rotation of the (whole) molecule \(\Rightarrow\) dof = 2 (linear), resp. dof = 3 (angular) per molecule, for one mole each contributing with \((1/2) R\).
Oscillation between all atoms in molecule \(\Rightarrow\) dof = \(3N-5\) (linear), resp. dof = \(3N-6\) (angular) per molecule, for one mole each contributing with \(R\).
Excitation depends on \(T\), vibration restricted to high \(T\) (IR spectra)
All findings can be well understood by the equipartition law for which the general proof will be discussed in a later chapter.
Examples:
- Monatomic: \((3/2) R\)
- Diatomic: \((3/2) R + (2/2) R + R =(7/2) R\)
- Three-atomic:
  Linear: \((3/2) R + (2/2) R + 4 R = (13/2) R\) (cf. Fig. 2.7 a)
  Angular: \((3/2) R + (3/2) R + 3 R = (12/2) R\) (cf. Fig. 2.7 b)

Here we will just add some explanatory hints as well as some specialties related to intermolecular hydrogen bonds:

Oscillations/vibrations contain kinetic and potential energy, hence in the heat capacity they count twice.
Vibrations can be described by symmetric / asymmetric valence- and deformation vibration modes, the so-called normal modes, using a representation with independent coordinates.
Rotation around the axis of linear molecules is not a significant contribution to \(C_V\) due to the minimum uptake of energy.
Hydrogen-containing polar molecules like ethanol, ammonia, and water have powerful, intermolecular hydrogen bonds when in their liquid phase. These bonds provide another place where heat may be stored as potential energy of vibrations, even at comparatively low temperatures. Hydrogen bonds account for the fact that liquid water stores nearly the theoretical limit of \(3 R\) per mole of atoms, even at relatively low temperatures (i.e. near the freezing point of water).

With frame

Experimental data on the heat capacity