Enthalpy and heat capacity at constant pressure

2.8 Enthalpy and heat capacity at constant pressure

When heating a system, typically the volume \(V\) increases. Thus often it is more simple to conduct processes at constant \(p\) to get the interrelation between the heat \(q\) and a state function.
To analyze e.g. reaction products we can spontaneously create our system while it is thermally insulated, but in constant mechanical contact with a ”volume bath” at pressure \(p\). For example, we could create our system inside a thermally insulated chamber with one movable wall where the external pressure is fixed at \(p\).

In both cases in addition to the internal energy \(U\) of the system, we must also perform work \(p\, V\) in order to make room for the expanding system. The thermodynamic discussion of such systems needs the introduction of enthalpy \(H\):

\begin{equation*} \begin{split} H & = U + pV\\ \Rightarrow dH & = dU + d (p\, V)\\ & = \delta q - p dV + p dV + V dp = \delta q + V dp = \delta q_p \end{split} \label{eq:def_H} \end{equation*}

(2.20)

Figure 2.4: Schematic representation of enthalpy \(H\) and inner energy \(U\) vs. temperature \(T\).

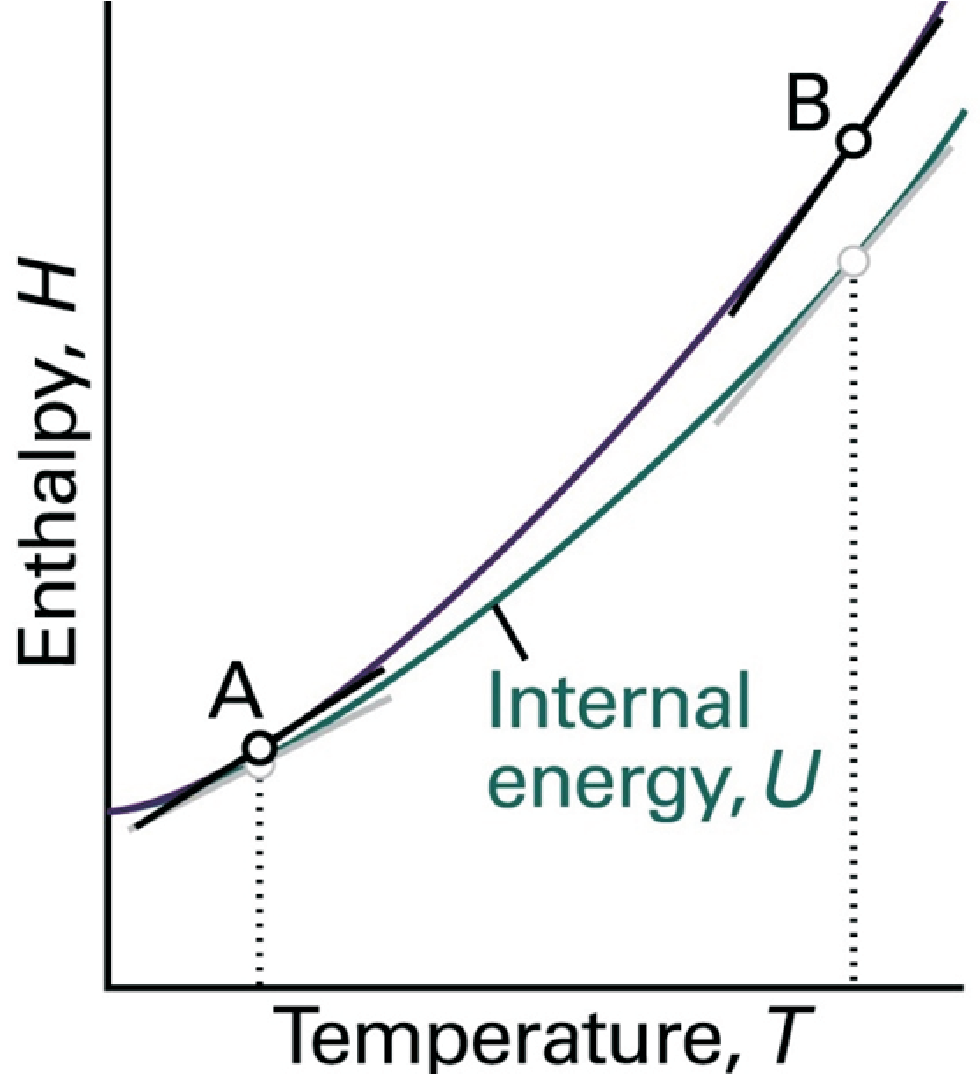
so \(\Delta H = q_p\) is the heat for systems under isobaric expansion.

The enthalpy is important for chemistry, it describes reactions in an open container.
For solids and liquids: \(\Delta H \approx \Delta U\).
Completely analogous to Eq. (2.8) we find the exact differential

\begin{equation*} dH = \left(\frac{\partial H}{\partial T} \right)_p dT + \left(\frac{\partial H}{\partial p} \right)_T dp \label{eq:dH_Tp_1} \end{equation*} (2.21)
Consequently the heat capacity for isobaric processes is

\begin{equation*} dH = \left( \frac{\partial H}{\partial T}\right)_p dT = C_p dT \label{eq:Cp_HT} \end{equation*} (2.22)
The perfect gas has no interactions. Thus, no change of \(T\) in the course of chemical reactions (no caloric effect) is expected, i.e.

\(\qquad \;\Delta_r T\): Change of \(T\) during a reaction \(\approx 0\). As a consequence

\begin{equation*} \begin{split} \Delta_r H & = \Delta_r U + \Delta_r(pV)\\ & = \Delta_r U + \Delta_r (n\, R\, T)\\ & = \Delta_r U + n \, R \Delta_r T + R \,T \Delta_r n \approx \Delta_r U + R \,T \Delta_r n \\ \end{split} \label{eq:DrH} \end{equation*}

(2.23)

As illustrated in Fig. 2.4 generally \(C_P \gt C_V\) since at constant volume all of the heat added is solely used to raise the temperature.
Several experimental approaches exist with similar working principles as the adiabatic bomb calorimeter:

Differential Scanning Calorimetry (DSC):
Here a well defined heating rate \(\alpha = \Delta T/t\) is enforced and basically the heating power is monitored.
Differential thermal analysis (DTA) / Thermo-gravimetry (TG):
Simultaneous measurement of \(\Delta m\) and \(\Delta T\).