Heat and heat capacity

2.7 Heat and heat capacity

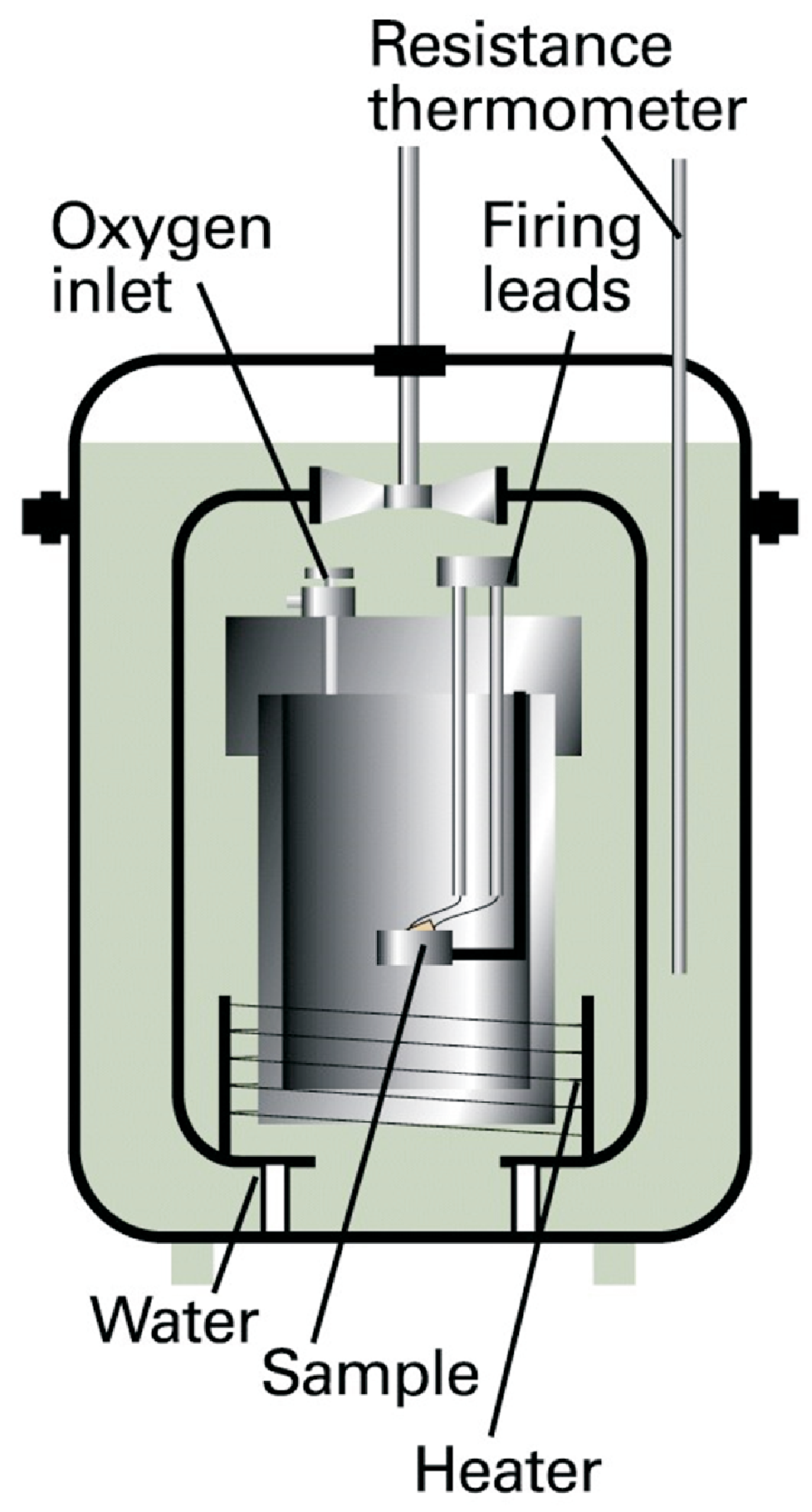
According to the zeroth law (cf. section 1.4) temperature is always a state variable. According to the first law, inner energy is always a state variable, so heat capacity is for all systems a reasonable information. Here we will discuss precise measurements for the heat capacity, more correctly \(C_V\), i.e. the heat capacity at constant volume \(V\), i.e. at isochoric condition. Typically our system is a sample within a bomb with constant volume \(V\) as shown in Fig. 2.3.

Figure 2.3: Adiabatic bomb calorimeter for precise heat capacity measurements.

Since no expansion work is performed we get \(\Delta U = q_V\). Next we transfer a defined amount of energy to the sample, e.g. electrically (\(w_{el} = q\, \Phi\)) or by a combustion reaction (via an oxygen inlet). In principle just \(\Delta T\) of the sample has to be monitored and an insulation is needed to ensure that no heat (energy) is transferred to the surrounding. Actually such perfect insulation is difficult, so an adiabatic bomb calorimeter is used for precise measurements:

The bomb is surrounded by water.
Both temperatures, \(T_{calorimeter}\) and \(T_{water}\) are measured, and by heating of the water \(T_{calorimeter} = T_{water}\) is enforced at any moment.
Thus no heat transfer from the sample (system) to the water (surrounding) exists, i.e. adiabatic boundary conditions are enforced.
The \(C_V\) determined by such an experiment is truly the sum of \(C_{V,substance} + C_{V, calorimeter}\). The latter must be determined beforehand by measuring reference substances.

In summary

\begin{equation*} \begin{split} dU & = \delta q + \delta w = \delta q + \delta w_{vol} + \delta w_{el} = 0 + 0 + \delta w_{el}\\ \Rightarrow dU & = \delta w_{el} = C_V dT \Rightarrow \Delta U = w_{el} + C_V \Delta T \\ & \quad \mbox{resp.} \quad C_V = \left( \frac{\partial U}{\partial T}\right)_V\\ \end{split} \label{eq:Cv_bomb} \end{equation*}

(2.19)

Obviously low \(\Delta T\) means large \(C_V\). As we will see in the subsequent sections the heat capacity provides highly relevant information about the structure of molecules of gases. In addition one can analyze phase transformations using the heat capacity: for first order phase transitions \(T\) stays constant and thus \(C_V \rightarrow \infty\).