Temperature and temperature scales

1.4 Temperature and temperature scales

Temperature is the most important and most easily measurable property directly related to thermodynamics.

A temperature difference indicates the direction of heat flow.
Boundary conditions are often chosen to either allow heat flow, i.e. diabatic (Greek: flowing through) or not allow heat flow, i.e. adiabatic (Greek: not flowing through). An example for an adiabatic system is a vacuum flask resp. Dewar vessel (vacuum is no thermal conductor).
Thermal equilibrium is characterized by the same temperature everywhere in the system. The ”Zeroth Law of Thermodynamics” states: If systems A, B and A, C are in thermal equilibrium, then C is also in thermal equilibrium with B, i.e. ”\(T\) is a state function” and \(T\) is transitive. This zeroth law ensures that meaningful temperature measurements are possible.

Any temperature measurement is based on a property \(\Gamma\) which should scale linearly with \(T\). For example the Celsius scale \(\Theta\) defines two specific states of water: 0 \(^{\circ}\)C (freezing point of water) and 100 \(^{\circ}\)C (boiling point of water) and a selection of 100 equally spaced units in-between, so

\begin{equation*} \Theta(\Gamma) = a\; \Gamma(\Theta) + b; \quad 0^{\circ}\mbox{C} = a\; \Gamma_0 + b \;, \quad 100^{\circ}\mbox{C} = a\; \Gamma_{100} + b \quad \Rightarrow \quad \Theta(\Gamma) = 100^{\circ}\mbox{C} \frac{\Gamma - \Gamma_0}{\Gamma_{100} - \Gamma_0} \end{equation*}

(1.6)

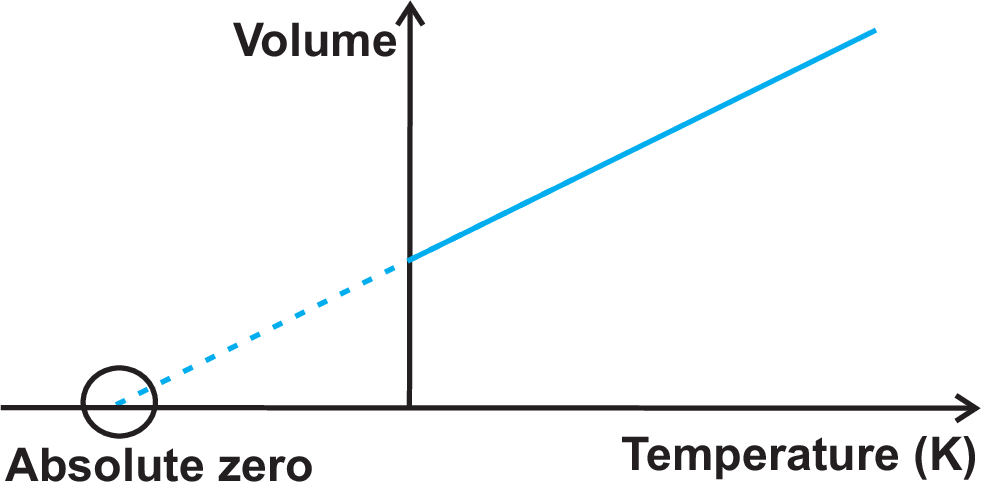
The perfect gas (or thermodynamic) temperature scale uses the perfect gas equation. Result of observations (which holds for all gases if \(p \rightarrow 0\), excluding possible non-linearities due to interactions and thus making temperature measurements independent of the working substance):

Figure 1.1: The Kelvin temperature scale illustrating the absolute zero temperature

A) \((pV)_T = const. = f(T)\); B) \((pV)_{T \rightarrow 0} = 0\). This implies a new zero point: 0 K (= –273.15 \(^{\circ}\)C); C) No non-linearity and substance dependency for \((pV)\) at low \(p\) (for perfect gas). The reference value of the perfect gas scale and the Celsius scale are slightly distinct: for the perfect gas scale the triple point of water (and not the boiling point) is the reference since this point in the phase diagram implies the absence of pressure dependencies. Since \(\left(\frac{\partial\, (pV)}{\partial\, T} \right) = const.\) the measurement of the product \(p\,V\) at low pressure can be chosen as an accurate temperature measurement:

\begin{equation*} \frac{T}{T_{ref}}= \lim_{p \rightarrow 0} \frac{pV}{(pV)_{ref}} \quad \Rightarrow \quad T / \mbox{K} = \Theta / ^{\circ}\mbox{C} + 273.15 \end{equation*}

(1.7)