7.1.2 A Closer Look at a Gyro

Working Principle

We have already seen that there is more than one way to make a MEMS gyro. Here we look at a concept that is used quite a bit and pursued at the ISIT, the Fraunhofer Institute for Si Technology in Itzehoe, a partner of the Inst. of Materials Science and Technology of the CAU.

The basic concept is to use the Coriolis force, always present in rotating systems, to induce a response in a moveable mass held by springs.

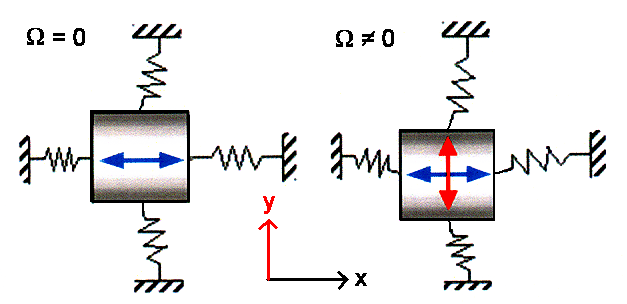
This is done by having a mass suspended on two orthogonal set of springs as schematically shown below. The mass is driven by some mechanism to oscillate in x-direction with constant amplitude. The frequency of the driving force is chosen in such a way that the system is close to its resonance frequency to ensure large amplitudes and therefore signals. As long as the the car or whatever moves with constant speed (in the x-y-plane to keep things easy), that is all that happens: The sensor mass oscillates in x-direction only.

Picture courtesy of ISIT

If we now imagine some rotation with angular velocity W around the z-axis perpendicular to the x-y-plane (our car is driving into a curve) a Coriolis force F_Cor develops, given by

F_Cor	=	2 · m · (v × W)

This Coriolis force drives our mass into the y-direction and thus will produce an oscillation in y-direction as shown above. The oscillation amplitude in y-direction then will "somehow" be coupled to the angular velocity W. Again, we try to work under resonance conditions because that gives higher sensitivity.

The resonance frequencies of the two oscillation modes (one in x-direction, the other one in y-direction) do not have to identical. In fact, we will take care to make them somewhat different.

So all we have to do now is to "somehow" measure the amplitude of the y-direction oscillation and figure out how it relates to W Also, not to forget, we have to figure out how todrive the oscillation in x-direction with constant amplitude "somehow". And after all that figuring is done, we have to make and package the system "somehow" - and sell it for 10 € or so.

For the first "somehow" we need a lot of physics and Math. At the most simple level we need to delve into the "driven damped linear oscillator" theory, contained in the following differential equation expressing Newtons first law:

m ·	d²x dt²	+ k_F · m ·	d x d t	+ k_s · x	=	F₀ · cos(w_D · t)

We have m=mass of the oscillating body, k_F=friction or damping constant, k_s=spring constant, F₀=amplitude of the driving force, w_D=frequency of the driving force.

This is a standard problem in more elementary mechanics and this link contains all you actually should know about this. Solving the equation gives the momentary location x(w, t), the amplitude X₀(w), and the velocity v=dx(w, t)/dt needed in the Coriolis force equation.

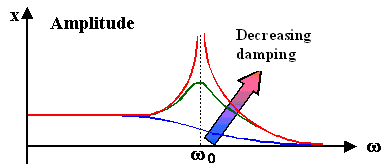
Looking just at the amplitude of a driven damped linear oscillator, we have the following, hopefully familiar picture:

Depending on the degree of damping or friction, we will have very large to relatively small amplitudes at the resonance frequency w₀

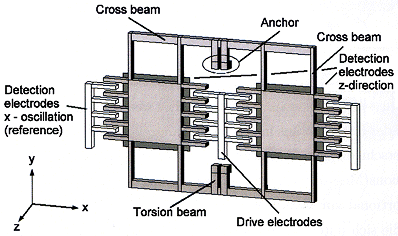
Obviously we need to know m, k_s, and k_F to go on. So let's look at an actual gyro in a very simple and by now (2007) outdated version:


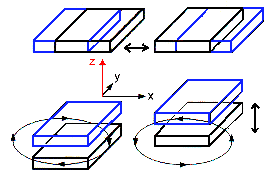	The two oscillation modes. The ellipses shows the combined effect
Pictures courtesy of ISIT

First thing to realize is that the oscillating mass is not the orderly mass point of basic mechanics but some extended piece of probably Si with a complex shape. The second thing to realize is that there are no neat little springs. The "beams" that define parts of the oscillating mass are also part of the "spring".

Being sophisticated Materials Science students, we know that the points raised above are no major problems. There are ways to calculate (numerically if necessary) how that contraption oscillates. The "spring" results from the mechanical properties of Si; Young's modulus will come up for sure. That takes care of m and k_s "somehow".

Good enough. But what about the k_F, the friction or damping constant? Now we are in deep water - or can you make an educated guess on that topic? No, you cannot - neither can I. Suffice it to say that the main friction or energy dissipation mechanism, is "air damping" i. e. the kind of damping you experience if you fawn a fan around.

That offers an opportunity and a problem: Adjusting the pressure inside the packaged chip allows to pick just the right damping for optimal functionality (that we "somehow" determined). That is the opportunities and that is what we actually really do. The problem is: How can you guarantee that this pressure will stay at its necessary value for 20 years or so? This is a first aspect of one of the tougher problems in MEMS: How to ensure long-time reliability.

Closer to Reality

Now let's take a look at the real thing in a relatively simple, but by todays R&D standards outdated, version:

Picture courtesy of ISIT

What you see is

A formidable problem in modelling the oscillatory behavior of that contraption with the aim of coming up with an optimal design.
An equally formidable challenge in making what you designed.

And we haven't even discussed how the driving and the signal detection works. But that is obvious from just looking at the picture above or the detail of the drive given below:

Driving the oscillation is obviously done electrostatically. The fixed part of the comb is supplied with some alternating voltage, changing the charge from plus to minus at the driving frequency, while the movable part is kept at a fixed charge=potential. This will lead to alternating attractive and repelling forces - the oscillator is driven accordingly

Picture courtesy of ISIT

Detection is done capacitively. The interdigitated finger structure at the outside for the reference signal detection is just a capacitor with an (alternating) capacity that depends on how deeply the fingers penetrate in the x-direction,

The two "large" plate under the outside fingers also form a capacitor with an (alternating) capacity that depends on how far the fingers are away in the z-direction.

In total we get easy-to-process AC signals with frequencies around the two resonance frequencies of the major oscillation modes. One signal we use for a feed-back loop that keeps the oscillation amplitude in the x-direction constant (or at whatever value we like), the other one contains the information we are after: the angular velocity W.

	Reality

	What does a real gyro, one we can buy now (2007) look like, and what are the salient points in designing and making it?
		Forget it. Let's just say that there is a lot more to designing and making a competitive gyro than we can discuss in the limited space here. There are people out there (called Materials Scientists and Engineers) who know how to do this. One day, if you keep at it, you might join their ranks.
		Just one example for what that could mean: The pictures here are mostly form the 2007 PhD thesis of Dr. O. Schwarzelbach (ISIT) who got his degree with an involved analysis (plus first designs) of a gyro relying on non-linear oscillatory behavior.