 |
Reibung, oder besser Energiedissipation, ist wichtig für die Art der Gleichgewichte, über die wir hier nachdenken.
Denn nur durch Reibung ist dafür gesorgt, dass sich nach einiger Zeit in klassischen
Systemen nichts mehr bewegt. |
|
 |
Ohne Reibung würde der im Hauptstrang gezeigte Massenpunkt
in einem Potentialtopf für immer hin-und herschwingen. |
|
 |
Betrachten wir nur diese Schwingung, wäre
der Massenpunkt dann auch im Gleichgewicht - es ändert sich schwingungsmäßig dann ja nichts mehr. Aber der
Begriff "Gleichgewicht" ist nur für (statistische) Systeme sinnvoll,
und sobald der Massenpunkt nicht mehr ideal isoliert ist kommt Reibung dazu; Gleichgewicht wird dann "Ruhe" (für
den Massenpunkt) sein. |
|
 |
Wie auch immer, bei klassischen Systemen haben wir immer
Reibung, und ein statisches Gleichgewicht ist sinnvoll, leicht vorstellbar und fast ohne begriffliche Probleme. Das "fast"
bezieht sich auf die Frage: Wo ist jetzt eigentlich die Energie, die in der Schwingung steckte? |
 |
Wie ist das nun im Atomaren? Gibt es zwischen den O2 und N2
Molekülen in der Luft, die uns umgibt, so was wie Reibung im klassischen Sinn? An was und wie "reibt" sich
unser im Potentialtopf schwingendes Atom? |
|
 |
Gottseidank gibt es die klassische
Reibung im Atomaren nicht! Denn dann würden nach einiger Zeit alle Moleküle ruhig am Boden liegen. Man muß
sich nur mal eine Art von dreidimensionalem Flipper mit vielen Kugeln gleichzeitig vorstellen, um das sofort zu sehen. |
 |
Wir nehmen einfach mal zur Kenntnis: Es gibt im Atomaren
keine Reibung im klassischen Sinne! |
|
 |
Das ist einfach zu sehen: Reibung im klassischen Sinne
hieße z.B., dass ein im Potentialtopf der Bindung schwingendes Atom eine Kraft FR
erführe, die mit negativem Vorzeichen proportional zu seiner momentanen Geschwindigkeit v wäre;
FR = –kR · v. |
|
 |
Das kann und darf nicht sein, denn dann würde die Amplitude und damit die Energie kontinuierlich
abnehmen - sie muss aber irgendwie gequantelt sein. Außerdem woher soll diese Kraft denn kommen? Es gibt nur die Bindungsnachbarn,
und die produzieren keine ominöse Reibungskraft. Und wo bleibt die Energie? |
 |
Reibung im klassischen Sinne bewirkt immer
nur eines: Energie, die in einer geordneten Bewegung steckt, wird aus diesem System
"irgendwie" herausgezuzzelt und der "Umgebung" als Wärme, d.h. als ungeordnete
kinetische Energie zugeführt. Reibung ist in diesem Sinne ein Energietransformator, ein Gleichmacher, ein Entropieerzeuger. |
|
 |
Das ist das allgemeine Phänomen der Energiedissipation
- und klassisch äußert sich das dann als Reibung. |
 |
Wie das atomar funktioniert ist im Grunde einfach zu sehen. Wir lassen mal gedanklich
einen Kristall über einen anderen gleiten - d.h. ein Körper rutscht auf einem anderen herum. |
|
 |
Klassisch werden wir Reibung erfahren; wir schauen aber mal bei sehr hoher "Vergrößerung"
was wirklich passiert. |
|
 |
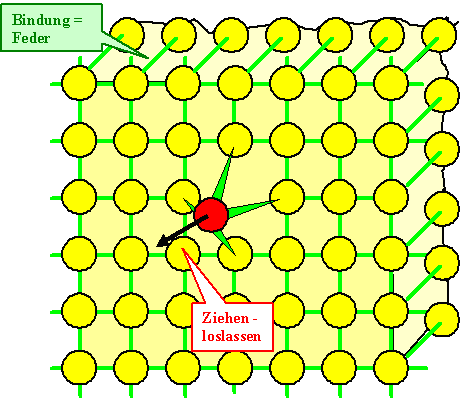
Solange die beiden Kristalle nicht so fest aufeinandergedrückt werden, dass bei einer
Relativbewegung plastische Verformung oder gar (mikroskopischer) Bruch erfolgt, können bestenfalls die Atome der Randschicht,
die von den Atomen des anderen Kristalls "angezogen" werden, bei einer Relativbewegung etwas aus ihrem Gleichgewichtsabstand
ausgelenkt werden. Aber früher oder später "schnalzen" sie zurück. Das sieht dann stark vereinfacht
so aus: |
| | |
|
|
 |
Es ist unmittelbar klar, was geschieht wenn das herausgegriffene Atom "zuückschnalzt":
nach kurzere Zeit wackeln alle Atome, die im Bild gezeigte lokalisierte elastische (= potentielle) Energie wurde auf alle
Atome "dissipiert", d.h. verteilt. |
|
 |
Das ursprünglich ausgelenkte Atom wird seine Schwingungsamplitude entsprechend verringern
- im Mittel genau so wie es mit klassicher "Reibung" beschrieben würde. |
 |
G. A. Tomlinson hat
diesen Mechanismus bereits im Jahr 1929 beschrieben. |
|
 |
Aber erst jetzt (2002) wurde der Effekt direkt gemessen - von zwei Augsburger Wissenschaftlern,
die mit Hilfe eines Rasterkraftmikroskops ein einzelnes Atom über eine Kristalloberfläche
"schleppten". |
| |
|
© H. Föll (MaWi 1 Skript)
![]() 5.1.2 Mechanisches und thermisches Gleichgewicht
5.1.2 Mechanisches und thermisches Gleichgewicht