Ramsdell Notation for SiC Polytypes

The Ramsdell notation for the stacking of hexagonal layers of atoms is simple (and not always extremely useful):

Specify the total number of layers contained in a (possibly large hexagonal) unit cell and then add the letter H, C or R) to denote the over-all lattice type as being hexagonal , cubic, or rhombohedral , respectively.

The most simple variants are thus

2H for the hexagonal close packing, i.e. for a ABABA.... sequence in the "ABC" notation familiar from Matwiss I for the hcp Bravais lattice
3C for the cubic close packing, i.e. the ABCABCA.... sequence of the fcc Bravais lattice.

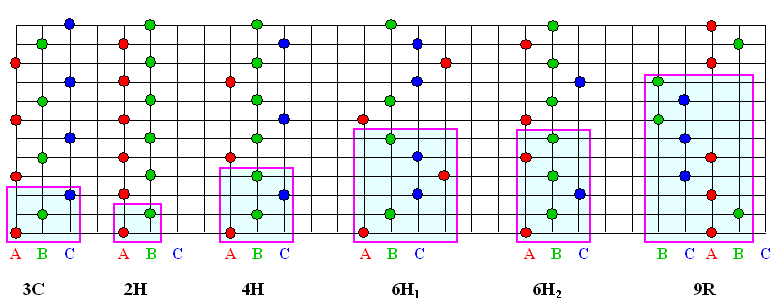
The designation "6H-SiC " thus means that we have 6 layers in some stacking sequence that follows the basic rules (no "head-on-head" configuration; B or C after A; A or C after B, ...) and produces an unit cell that is hexagonal.. Let's look at examples to get the idea:

Now you have problems:

1. There might be more than on way to stack, e.g., 6 planes with a hexagonal unit cell. The designation 6H thus may not be unique.

This is indeed the case as shown above. Subdivisions are needed; we have, e.g., the 6H₁ and 6H₂ configuration. Just how many possible subdivision are possible is not easily seen, however.

Note: While all "legal" stackings of 6 planes produce a unit cell of the hexagonal type, it is not necessarily the smallest Bravais lattice of the structure, not to mention the smallest unit cell! Looking at smallest unit cells, you might rather end up with a cubic or rhombohedral lattice. For the 3C structure this is sufficiently clear, for the others you have to believe it (or to sit down and do serious crystallography). This leads directly to the second question:

2. It is easy, of course, to generate all kinds of allowed stacking sequences for a given number; say 9. Repeating the sequence will produce a crystal with some Bravais lattice. But is it possible to have all kinds of combinations? What is possible? Is there besides a 9H also a 9C, and/or a 9R configuration? Could other Bravais lattices come up?

Who knows. What kind of lattice you get, e.g., is not directly obvious from the picture above (at least not to me). There will be restrictions, of course; e.g. since the Si- and C-Atoms must always be tetrahedrally coordinated in any allowed stacking sequence. It appears that you always have only cubic, hexagonal and rhombohedral Bravais lattices to deal with.

So we will let the matter rest, assuming that crystallographers have figured it out and that, if necessary, the questions above can be answered unambiguously.

There are many more polytypes besides the ones shown in the picture. A more common one is actually 15R (stacking sequence ABCBACABACBCACB).

Most stable is, perhaps, the 3C structure (also known as b-SiC) at lower temperatures, and the 6H modification (a-SiC) above about 1800 ⁰C. In other words, we have a phase transformation upon crossing a certain temperature.

But there are many more variants; the list goes up to 39H, 39R, 45R and 51R.

This brings up an obvious and difficult question:

How, for an extreme example, a growing 51R crystal "knows" what has happened 51 stacking planes below, when it adds another layer, is still a kind of mystery. The crystal must "know" somehow, otherwise it could not do the proper stacking - think about it.

Considering that we usually may safely neglect interactions between second-nearest neighbors in a lattice, this is a tough nut to crack, indeed!

With frame

10.1.1 Silicon Carbide - Material Aspects