6.1.3 Oscillation and Second Laser Condition

6.1.3 From Amplification to Oscillation: Second Laser Condition

	So far we have the principle of the amplification of light by stimulated emission. Making a laser in the conventional sense of the word still requires to produce a light beam with a "battery" – not with some input light.
		Since we nevertheless need at least some input light, this is the same task as to produce an oscillator from an amplifier in electronics, and the solution of this task is achieved along identical lines: Feed back one frequency from the output of the amplifier to the input and make sure it is in phase (or, as we say for light, "coherent"). Thus, we have to take . . .

A General Look at Feedback and Oscillations

Feeding one frequency from the output back to the input will lead to an amplification of this frequency.

Since then also the intensity of the feedback signal increases, this one frequency will become more amplified, and so on ... – pretty soon your system is now an oscillator for the frequency chosen. That is, you feed back a large enough part of the output to account for losses that may be occurring in the feedback loop so that still sufficient amplitude is left to drive the amplifier. The essential parts are shown in the drawing:

If you think about this, you will discover a problem. If there is enough signal at the input, the output will go up forever or until a fuse blows – there is no stability in the system

We need some kind of servo mechanism that adjusts the amplification factor to a value where only the losses are recovered by amplification, so that a stable, preferably adjustable output amplitude is obtained.

This is clear enough for electrical signals, but how do we do this with light? Well, we do everything with mirrors:

1. The feed back part in general.

2. The coherency requirement.

3. The selection of the frequencies.

4. The guidance of the light including the "beam shaping " of the output.

The 4th point is new – after all, electrical signals go to wherever the wires go, but with light we have to make sure we get a single beam if we like to have one.

We first look at the general principle of light feedback without worrying about the three other points (which we throw in afterwards).

Feedback with Mirrors

All we have to do is to put the piece of semiconductor that is supposed to amplify the light by stimulated emission between two partially transparent mirrors

The whole system then looks like this.

Let's look at this in a quantitative way. We start the analysis by feeding some light with the intensity I₀ (from the left) to the semiconductor which we keep in a state of inversion by constantly supplying the necessary electrons and holes. It will be amplified along its way through the semiconductor (length L ) if we exceed the threshold for amplification and emerge with the intensity I₁ on the right

Parts of I₁ will be reflected; this intensity we call I₂, it is given by

I₂	=	I₁ · R₁

R₁ is the reflection coefficient for mirror 1. For R₁ = 1 all the light will be reflected, for R₁ = 0 all the light will be transmitted.

The transmitted intensity is then simply I₁ · (1 – R₁) as indicated in the drawing.

But now we have light traveling (and getting amplified) from right to left.

It will emerge with the intensity I₃, some of it (I₄ = I₃ · R₂) will get partially reflected and run through the crystal, and so on and so on.

Eventually, we will reach a steady state with all intensities being constant. Let's see what that will be.

First we write down all the relations for the intensity that we have, using the formula from before that links the output to the input:

I₁	=	I₀ · exp[(g – a_i) · z]

I₂	=	I₁ · R₁

I ₃	=	I₂ · exp[(g – a_i ) · z]

I₄	=	I₃ · R₂

We dropped some indices for ease of reading and obtain immediately for, e.g., I₄

I₄	=	I₀ · R₁ · R₂ · exp[(g – a_i) · 2L]

To make life easy, we use a small trick and assume R₁ = R₂ = R (a reasonable choice automatically fulfilled if we take as partially reflecting mirrors simply the surfaces of the crystal).

Next, because light not reflected back into the crystal is lost, we express the reflection part in terms of losses by smartly defining the quantity

a_R	:= –	1 2L	· ln (R₁ · R₂)	= –	1 2L	· ln (R²)	= –	1 L	· ln R

Since R < 1, a_R is always positive because of the minus sign. This gives us

R ₁ · R₂ = R² =		exp (–2 · a _R · L)	Þ	exp (–a _R · L) = R

The losses of the external output due to the partial reflection as it would appear to an "outside" observer thus are assigned to the crystal, too, and the factor ½ or 2, respectively, appears because the light travels twice through the crystal.

This gives the final form for I₄:

I₄	=	I₀ · exp	æ è	[g – (a_i + a_R)] · 2L	ö ø

What does this equation tell us? It contains two essential pieces of information:
1. The condition for starting the process, and
2. the conditions for the stationary state.

Let's look at this in detail:

The requirement for starting the process, i.e. for starting the oscillator, is that after one cycle (from I₀ to I₄) we must have recovered I₀. Or, in formal words, the starting condition is

I₄	³	I₀

[g – (a_i + a _R] · 2L	³	0

This then defines a threshold value g _th for the gain factor g which is given by

g_th	=	a_i + a_R = a_i –	1 L	· ln (R)

If the system has a gain coefficient above this value, one photon will be enough to start the process, and since one photon is always around, the system will then start to produce light on its own without outside help.

Since the gain coefficient is a strong function of the carrier density, this also means that light production will start automatically as soon as the carrier density (= electrons in the conduction band) reaches a threshold value n^e_th. And that density is larger than the density needed for inversion or transparency.

Now to the second questions: What determines the stationary state, or how much light is actually produced? Naively, we would expect that after the start, the intensity will go up in every cycle, and if nothing changes, it will go through the roof to infinity .

This, of course never happens, because it would imply that you inject an infinite amount of new carriers for stimulated emission to occur at the required rate. Clearly then, the limited supply of carriers will bring down the gain coefficient and some steady state can be expected for some specific carrier density.

Steady state simply means that your gains are exactly identical to the losses, and this means I₄ = I₀.

This is essentially the same equation as for the start of the process (only the ">" sign is missing) and we obtain the final result for the gain coefficient in stationary state, g_stat, and by inference for the carrier densities n^e_stat :

g_stat	=	a_i –	1 L	· ln R	=	g_th

n_stat	=	n^e _th

While this looks deceptively simple, it provides a lot of open questions. First of all, we have only met our first requirement from above for an oscillator producing coherent light at a defined frequency; the other ones are still open. Then we might ask ourselves, exactly how the crystal manages to regulate the gain coefficient, or how the intensity evolves with time?

Since these questions are interrelated, we first look at how requirements 2–4 can be met.

Requirement 4 is easy now:

The photons travel according to the laws of geometric optics (in a first approximation). With planar mirrors perpendicular to the z-direction, they just run back and forth.

If we use inclined mirrors, or bent mirrors, or fibre optics, things may become complicated, but in principle we know how to treat it.

We therefore will not worry about this point any more, but simply stick to the simple back-and-forth light path arrangement shown in the drawing .

Requirements 2 and 3 can be met with the same basic trick:

Chose the (optical) distance between the mirrors to be a multiple of half of the wave length you want. If you use external mirrors you must take into account that the wave length in air is different from that in the crystal, that's were the qualifier "optical" comes in.

If we simply use the surfaces of the crystal as mirrors, the length between the mirrors is L = length of the crystal and the condition given above then is

L	=	m · l _air 2n_ref	=	m · l 2		m = 1, 2, 3, 4, ...

With l_air = wave length in air, l = wave length in the crystal, n_ref = refractive index of the crystal.

If we do this, we will have a coherent beam of light travelling in z and –z-direction with a wave length l_air that is
1. given by the equation above, and
2. lies in the wave length region where the gain factor is sufficiently large.

While the first condition would still allow many wave lengths, the second conditions normally admits just one. But why?

Simply because any two mirrors at any distance define a resonant structure and that is why such a system is called a Fabry- Perot resonator (or interferometer). Only light with wave lengths given by the Fabry-Perot resonance condition l = 2nL/m can exist inside a "Fabry-Perot" as a standing wave.

This is best seen by looking at what would happen to light with a "wrong" wave length. Every time it travels through the system, its phase is shifted to some extent, and pretty soon you have a wave with the phase – p for any wave with the phase 0 and destructive interference will cancel everything except waves with phases that fit.

This is the same old principle that governs diffraction of electrons or X-ray beams in crystals, all musical instruments, and, if you believe Richard Feynman , just about everything else, too.

In other words, we already met the 2. and 3. requirement (without noticing, perhaps), but not necessarily at the optimal frequency which is of course the frequency with the highest gain factor g( n).

Or in yet other words: While the picture of light waves travelling in and out of the crystal is not wrong, what we really have after a very short time is a standing wave inside the Fabry-Perot resonator with usually just one dominating wavelength from the multitudes possible. It looks like this

Shown is the intensity, i.e. the square of the amplitude (and not the amplitude as a function of time) of a standing wave with a wave length considerably smaller than the length of the crystal – as we will encounter it in reality.

The wave length is determined by the condition that 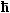w »E_g, or, with w = c/(n_ref · l)

h · c n_ref	»	E_g

Whichever way we describe the light – by its wave length l, its angular frequency w , or its energy 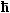w, we can always index these quantities now with a "g" for "gap" and know how to calculate the numerical values for, e.g. w_g.

Taking the requirement for the threshold gain and the admissible wave lengths together is called "second laser condition", i.e.

g_stat	=	a_i + a_R	= a _i –	1 L	· ln R	=	g_th

L	=	m · l_g_air 2n_ref	=	m · l_g 2

Since g is a function of the wave length l_g or the frequency n_g, respectively, and the carrier density n^e ( do not mix it up with the refractive index n_ref !); g(l, n^e), we can combine both equations into

a_i + a_R	=	g(n_g, n^e_th)

What do we know about the quantities in this equation?

We know that a_i with its various components is primarily a function of the carrier density; we need its value at the threshold density n^e_th.

We can expect that the optical losses described by a_R are pretty much constant, but g(n, n^e) is a rather complicated function defined by integrals over densities of states times Fermi distributions and the like; we thus have a complex (integral) equation for the determination of n^e_th, our only unknown parameter at this point.

Computing n^e_th from the second laser condition can only be done numerically and requires good knowledge of the relevant quantities. We can get a rough estimate, however, by neglecting the frequency dependence and taking the maximum value of g at the fixed frequency, g^max. And for g^max we had the empirical equation

g_n^max	=	a · (n^e – n^e _T )

n^e_T was the transparency density, and a the differential gain factor, a material constant.

Inserting this equation for g(n_g, n^e_th) in the second laser condition from above yields a kind of (approximate) master equation for semiconductor lasers

n ^e_th	=	n ^e _T +	a_i + a_R a

It includes the first laser condition (which defined n^e _T) in the conditions for self-induced oscillations at the "right" frequency, parts of which are released to the outside world (this is the a _R part).

And, of course, what we will have as soon as the carrier density that we inject in our semiconductor crystal contained within a properly spaced Fabry-Perot resonator reaches the threshold is a LASER in the specific meaning discussed before.

This leaves us now with the big question: How do we make a semiconductor laser? Or, for that matter, a simple light emitting diode, which will turn into a laser if we put it inside a Fabry-Perot and crank up the injected carrier density "somehow".