 |
In principle, anything that emits electromagnetic radiation can be turned into
a "LASER", but what is a laser? |
|
 |
The word "LASER" was (and of course
still is) an acronym,
it stands for "
Light Amplification by S
timulated Emission of R adiation". By
now, however, it is generally perceived as a standard word
in any language, meaning something that is more than the acronym suggests (and we will therefore no longer
write it with capital letters)! |
|
 |
A laser in the direct meaning of the acronym is a black box that emits (= outputs) more light
of the same frequency than what you shine ( = input) on it – that is the amplifier
part. But the "stimulated emission" part, besides being the reason for amplification,
has a second, indirect meaning, too: The light emitted is exactly in phase (or coherent to) the light in the input. Unfortunately,
lasers in this broad sense do not really exist. Real lasers only amplify light with a very specific frequency – it's
like electronic amplifiers for one frequency only. |
 |
A laser in the general meaning of the acronym
thus produces intense monochromatic electromagnetic radiation in the wavelength region of light (including infrared and
a little ultra-violet; there are no sharp definitions) that is coherent to the (monochromatic) input. If you "input"
light containing all kinds of frequencies, only one frequency becomes amplified. |
|
 |
A laser in the specific meaning of everyday
usage of the word, however, is more special. It is a device that produces a coherent beam of monochromatic light
in one direction only and, at least for semiconductor lasers, without
some input light (but with a "battery" or power source hooked up to it). It is akin to an electronic
oscillator that works by internally feeding back parts of the output of an amplifier to the input for a certain frequency. |
|
 |
Before the advent of hardware lasers in the sixties, there were already "masers
" – just take the "m" for "microwave" and you know what it is. |
|
 |
And even before that, there was the basic insight or idea behind masers and lasers, and –
as ever so often – it was A. Einstein who described the
"Stimulated E
mission" part in 1917/1924. More to the history of lasers
can be found in an advanced module. |
 |
Obviously, for understanding lasers, we have to consider stimulated
emission first, and then we must look at some feedback mechanism.
|
 |
Understanding stimulated emission is relatively easy; all we
have to do is to introduce one more process for the interaction between light and electrons and holes. So far we considered
two basic processes, to which now a third one must be added: |
|
 |
1.
Fundamental absorption,
i.e., the interaction of a photon with an electron in the valence band resulting in
a electron(C)–hole(V) pair. |
|
 |
2.
Spontaneous emission
of a photon by the (spontaneous and direct) recombination of an electron–hole pair. |
|
 |
3.
Stimulated emission, as the third and new process, is simply the interaction
of a photon with an electron in the conduction band, forcing recombination and
thus the emission of a second photon, being an exact duplicate of the incoming one. |
 |
All three processes are schematically shown in the band diagram below. |
| |
|
 |
Looking at this picture, you should wonder why one obvious further process is
missing: How about an electron in the conduction band simply absorbing a photon? The electron could be moved up by the amount
hn in the conduction band, and would come back to the band edge by tranferring its surplus
energy to phonons. |
|
 |
This process does take place, but it is not very strong if we do not have many electrons in
the conduction band. More importantly: It is not necessary for "lasing", but rather detrimental – we will
cover it later. |
 |
Stimulated emission, however, is not just
the reverse of absorption. Again: Usually, photons interact with electrons in the conduction band by transferring
their energy to the electron, which moves the electron to some higher energy level in the band (or to the next
band, or, if the photons are very energetic (meaning X-rays), even out of the crystal) – which means that the
photons are absorbed . |
|
 |
On the contrary, stimulated emission is a resonant process;
it only works if the photons have exactly the right energy, corresponding to the energy that is released
if the electron makes a transition to some allowed lower level. Then, the two photons are exactly
in phase with each other (and propagate in the same direction). For semiconductors, this energy is pretty much
the band gap energy, because all conduction band electrons are sitting at the conduction band edge (more precisely, within
some small energy interval above EC
, of course), and the only available lower energy level are the free positions (i.e., occupied by holes) at the valence
band edge. |
|
 |
Stimulated emission thus may be seen as a competing process to the fundamental band–band
absorption process described before. But while all photons with an energy hn > Eg may
cause fundamental absorption, because there are many unoccupied levels above Eg,
only photons with hn = Eg (plus some small DE,
possibly) may cause stimulated emission. |
 |
Einstein showed that under "normal" conditions (meaning conditions not
too far from thermal equilibrium), fundamental absorption by far exceeds stimulated emission.
Of course, Einstein did not show that for semiconductors, but for systems with well-defined energy levels – atoms,
molecules, whatever. |
|
 |
However, for the special case that a sufficiently large number of electrons occupies an excited
energy state (which is called inversion), stimulated emission may dominate the electron–photon
interaction processes. Then two photons of identical energy and being exactly in phase
come out of the system for one photon going into the system. |
|
 |
The kind of inversion
we are discussing here should not be mixed up with the inversion
that turns n-type Si into p-type (or vice versa) that we encounterd before. Same word, but different phenomena! |
|
 |
These two photons may cause more stimulated emission – yielding 4, 8,
16, ... photons, i.e. an avalanche of photons will be produced until the excited electron states are sufficiently
depopulated. |
|
 |
In other words: One photon hn impinging on a material that
is in a state of inversion (with the right energy difference hn
between the excited state and the ground state) may, by stimulated emission, cause a lot of photons to come out of the material.
Moreover, these photons are all in phase, i.e. we have now a strong and coherent beam of light – amplification of
light occurred! |
 |
We are now stuck with two basic questions: |
|
 |
1. What exactly do we mean with "inversion", particularly with respect to
semiconductors? |
|
 |
2. How do we reach a state of "inversion" in semiconductors? |
 |
Let's look at these questions separately! |
 |
If you shine 10 input photons on a crystal, 6 of
which disappear by fundamental absorption, leaving 4 for stimulated emission, you now have 8 output photons.
In the next round you have 2 · (8 · 0.4) = 6.4 and pretty soon you have none. |
|
 |
Now, if you reverse the fractions, you will get 12 photons in the first
round, 2 · (12 · 0.6) = 14.4 the next round – you get the idea. |
|
 |
In other words, the coherent amplification
of the input light only occurs for a specific condition: |
 |
There must be more stimulated emission processes than fundamental absorption
processes if we shine light with E = hn = E g on a direct semiconductor
– this condition defines " inversion
" in the sense that we are going to use it. |
|
 |
Note that the light produced by spontaneous recombination of the electron–hole
pairs, generated by fundamental absorption, is not coherent to the input and does not count! |
|
 |
We only look at direct semiconductors, because
radiative recombination is always unlikely in indirect semiconductors, and while stimulated emission is generally possible,
it also needs to be assisted by phonons and thus is unlikely, too. |
 |
We will find a rather simple relation for the dominance of stimulated
emission, but it is not all that easy to derive. Here we will take a "shortcut
", leaving a more detailed derivation to an advanced module. |
| |
|
 |
Let's first consider some basic situations for inversion in full generality.
For the most simple system, we might have two energy levels E
1 and E2 for atoms (take any atom), the lower one (E
1) mostly occupied by electrons, the upper one (E2 ) relatively empty. Inversion then means that the number of electrons on the upper level, n2,
is larger or at least equal to n1. |
|
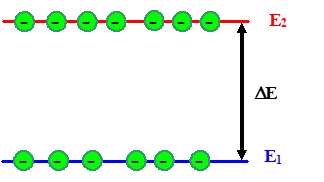 |
| Two-level system in inversion condition |
|
 |
In equilibrium, however, we would simply have |
| |
|
n2
n1 | = |
D2
D1 |
· exp (– |
DE
kT | ) |
|
|
|
|
| | |
| |
|
 |
Here, DE = E2 – E
1, and D1,2 =
the maximum number of electrons permitted on E1,2 (the "density of states").
|
|
 |
In words: In equilibrium we have far more electrons at E1
than at E2 . |
 |
For inversion to occur, we therefore must be very far
from equilibrium if D E is in the order of 1 eV as needed for
visible light. |
|
 |
However, stimulated emission would quickly depopulate the E2
levels, while fundamental absorption would kick some electrons back. Nevertheless, after some (short) time we would be back to equilibrium.
|
|
 |
To keep stimulated emission going, we must move electrons from E1
to E2
by some outside energy source. Doing this with some other light source providing photons
of the only usable energy DE would not only defeat the purpose of the game (since,
after all, that is the light we want to generate) – it also would never bring us back to inversion because of the
depopulation of E2 by stimulated emission. |
|
 |
In short: Two-level systems
are no good for practical uses of stimulated emission. |
|
 |
In semiconductors we could inject electrons from some other part of the device,
but a semiconductor is not a two-level system, so that is not possible. |
 |
What we need is an easy way to move a lot
of electrons to the energy level E2
without depopulating it at the same time. This can be achieved in a three-level system as shown below (and this was the way it was done with the first ruby laser). |
| |
|
 |
The essential trick is to have a whole system of levels – ideally a band
– above
E2, from which the electrons can descend efficiently to our single level E2
– but not easily back to E1 where they came from. Schematically, this looks like the figure on the right.
| |
|
 |
The advantage is obvious. We now can use light with a whole range of energies – always
larger than DE – to "pump"
(yes, this is the standard word used for this process) electrons up to E2 via the reservoir provided
by the third level(s). |
|
 |
The only disadvantage is that we have to take the electrons from E1.
And no matter how hard we pump, the effectiveness of the pumping depends on the probability that a quantum of the energy
we pour into the system by pumping will actually find an electron to act upon. And this will always be proportional to the
number (or density) of electrons available to be kicked upwards. In the three-level system this is at most D1.
However, if we sustain the inversion, it is at most 0.5 · D1, because by definition we then
have at least one-half of the available electrons on E2. |
| |
 |
It is clear what we have to do: Provide a
fourth level (even better: a band of levels) below
E1, where you have a lot of electrons that can be kicked up to E 2 via
the third level(s). It is clear that we are talking semiconductors now, but let's first see the basic system: |
| |
|
 |
We simply introduce a system of energy states below E 1 in the picture
from above. We now have a large reservoir to pump from, and a large reservoir to pump to. |
|
|
 |
All we have to do is to make sure that pumping is a one-way road, i.e. that there are no (or
very few) transitions from the levels 3 to levels 4. |
|
 |
This is not so easy to achieve with atoms or molecules, but, as you should have perceived
by now, this is exactly the situation that we have in many direct band gap semiconductors. All we have to do to see this
is to redraw the 4-level diagram at the right as a band diagram. To include additional information, we do this in
k-space. |
|
|
 |
We have the following general situation for producing inversion in semiconductors
by optical pumping: |
|
|
|
|
|
| |
|
 |
The
condition for inversion was that there were at least as many stimulated emission processes
as fundamental absorption processes. The recombination rate by stimulated emission we now denote R
se, and the electron–hole pair generation rate by fundamental absorption is Rfa.
We thus demand: |
| |
|
|
 |
In general, fundamental absorption and stimulated emission can happen in a whole range of
frequencies for semiconductors. While we expect that the electrons that are being stimulated to emit a photon will occupy
levels right at the conduction band edge, stimulated emission is not forbidden for electrons with a higher energy somewhere
in the conduction band. While these electrons are in the (fast) process of relaxing to EC
, they still might be "hit" by a photon of the right energy at the right time and place – it is just
more unlikely than at EC. |
 |
We thus must expect both rates, Rse
and Rfa, to be proportional to: |
| 1. |
The
spectral intensity of the radiation in the interesting frequency interval. |
|
 |
The differential frequency interval considered extends from n
to n + D
n; the spectral intensity in this interval we name u(n)Dn or, expressing the frequency n
in terms of energy via Ephot = hn, u(E)DE.
|
|
 |
This value, u(E)DE, divided by the
single-photon energy Ephot = hn, essentially gives the
flux of photons in this frequency interval (i.e., the number of photons arriving per second and per area, for short).
|
|
2. |
The density of states available for the processes.
|
|
 |
The probability that a photon with a certain frequency n
and therefore energy Ephot = hn
will be absorbed by an electron at some position E
1 in the valence band (i.e., close but not necessarily equal to EV
), will be proportional to the density of states in the valence band, DV( E1),
and to the density of states exactly Ephot above this position
in the conduction band, DC( E1 + hn). |
|
 |
Contrariwise, the probability that stimulated emission takes place, triggered by a photon
with energy hn, is proportional to the density of states in the conduction band and to the density of states hn below in the valence band. |
|
 |
This is a crucial part of the consideration – and a rather
strange one, too: That both
densities of states must be taken into account – where the particle is coming from and
where it is going to – is a quantum mechanical construct (known as Fermi's
golden rule) that has no classical counterpart. |
| 3. |
The probability that the states are actually occupied (or unoccupied). |
|
 |
The density of states just tells us how many electrons (or holes) might
be there. The important thing is to know how many actually are there – and this
is given by the probability that the states are actually occupied (necessary for absorption
or stimulated emission) or unoccupied (necessary for the transition of electrons to this state).
|
|
 |
In other words, the Fermi–Dirac distribution comes
in. In the familiar nomenclature we write it as f(E, EFe, T) or f(E,
EFh, T) with E Fe,h = quasi
Fermi energy for electrons or holes, respectively. |
|
 |
The crucial point is that we take the quasi
Fermi energies, because we are by definition treating strong non-equilibrium
between the bands, but (approximately) equilibrium in the bands. |
|
 |
We also, for ease of writing, define a direct Fermi distribution for the holes as outlined before and distinguish the different distributions by the proper
index: |
| |
| fe or h(E , EFe,h, T) |
= | |
probability that some level at energy E
is occupied by an electron or hole |
| | |
| |
| 1 – fe or h(E, EFe,h,
T) | = | |
probability that some level at energy E
is not
occupied by an electron or hole |
|
|
|
 |
Remember that "not occupied by a hole" always means "occupied by an electron"
– whereas the meaning of "not occupied by an electron" depends on what is referred to: Only for the valence
band this means "occupied by a hole"! (Do you also remember why this is so? If not: Think about charge neutrality!) |
 |
That is all. However, the density of states
are complicated functions of E, and the spectral density of the radiation we do not know – it is something that should come out
of the calculations. |
|
 |
But we are doing shortcuts here, and we do know that the radiation density will have a maximum
around hn = Eg = EC – EV.
So let's simply assume that the necessary integrations over u( E) · D(E)DE
will be expressible as Neff · u(n) ·
Dn with Neff =
effective density of states. Moreover, we assume identical Neff in the valence and conduction band.
|
|
 |
The rates Rse for stimulated emission and Rfa
for fundamental absorption then can be written as |
|
| | Rfa |
= |
Afa · Neff2 · u(n) · D n · |
æ
è |
1 – fh in V (E1 , EFh, T) |
ö
ø |
· | æ
è
|
1 – fe in C (E1 + hn, EFe
, T) | ö
ø |
| R se | = |
Ase · Neff2 · u(n) · Dn · |
æ
è |
fe in C (E1 + hn, EFe,
T) | ö
ø |
· | æ
è
|
fh in V (E1, EFh, T) |
ö
ø |
|
|
|
 |
The Afa and the Ase are the proportionality
coefficients and we always use fh in V if we consider carriers in the valence band and fe in C
if we consider the conduction band. |
 |
Enters Albert
Einstein. He showed in 1917 that the following
extremely simple relation always holds for fundamental reasons: |
| |
|
|
 |
We will just accept that (if you don't, turn to the advanced
module for a derivation) and now form the ratio Rse / Rfa.
The coefficients then just drop out and we are left with |
|
|
Rse
Rfa |
= |
[fe in C (E1 + hn , EFe,
T)] · [fh in V (E1, EFh, T)]
[1 – fh in V (E1, EFh, T)] · [1
– fe in C (E1 + hn, EFe,
T)] |
|
|
|
 |
With
some shuffling of the terms (see the exercise below) we obtain |
| |
|
|
 |
with E1 and E1 + hn
denoting some energy level in the valence or conduction band, respectively, implying hn ³
Eg (since for direct semiconductors, the smallest possible difference between some energy levels in
the valence band and some energy levels in the conduction band that are connected by a direct transition is Eg). |
 |
This is a rather simple, but also rather important equation. It says that we have
more stimulated emission between E1 + hn
and E1 than fundamental absorption between E1 and E1
+ hn if the difference in the quasi Fermi energies is larger than
the difference between the considered energy levels. |
|
 |
Thus, we have as the first
laser condition: |
|
|
|
|
 |
We call this "laser condition ", because "lasing"
requires inversion, i.e. that there are at least as many electrons at the conduction band edge as we have electrons
(not holes!) at the valence band edge. |
© H. Föll (Semiconductors - Script)