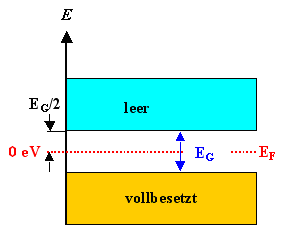
 |
Gegeben sei die folgende extrem vereinfachte Bandstruktur: |
| |
|
|
 |
Wir wollen damit ein bißchen den Umgang mit Fermiverteilung
und Ladungsträgerdichten üben. |
| |
1. Frage: Der spezifische Widerstand typischer Halbleiter liegt um
(1 - 1.000) Wcm; typische Beweglichkeiten liegen im Bereich m
= (500 - 5.000) cm2/Vs. |
|
|
Wir nehmen an, dass nur Elektronen im Leitungsband (dem nominell leeren Band) zur Leitung
beitragen können.Welche Ladungsträgerdichten
braucht man dazu im Leitungsband? |
|
Die notwendigen Ladungsträger müssen per thermischer Energie
aus dem vollbesetzten Valenzband den Sprung ins Leitungsband geschafft haben. Für Si gibt es im Leitungsband
schon "ganz unten" Platz für ca. Neff = 3 · 1019 Elektronen pro cm3
(Man nennt das: "effektive Zustandsdichte"). |
|
|
Angenommen, die Fermienergie ist genau in der Mitte
einer Bandlücke der Größe EG (wir setzen darauf dann den Energienullpunkt).
Dann ist die: |
|
2. Frage: Wie groß muss die Energielücke bei Raumtemperatur
(TR = 300 K) sein, damit die richtige Ladungsträgerkonzentration resultiert? Wie groß
bei 100 K oder 500 K? |
|
|
Vergleiche die Ergebnisse der exakten
Formel (= Fermiverteilung) mit der Boltzmann-Näherung. |
|
3. Frage: Wähle in Gedanken eine Temperatur, bei der genau ein Elektron den Sprung vom Valenzband ins Leitungsband schafft. Vergleiche die Wahrscheinlichkeiten,
dass genau ein
Platz im Valenzband nicht besetzt ist, mit der Wahrscheinlichkeit,dass genau ein Platz im Leitungsband besetzt ist. Begründe damit, warum die Fermienergie genau in der
Mitte der Bandlücke liegen muss! |
| |
|
© H. Föll (MaWi für ET&IT - Script)
8.3 Baendermodell und Materialeigenschaften 
Mit Frame