8.4 Zusammenfassungen zu Kapitel 8

8.4.1 Merkpunkte zu Kapitel 8: Leitfähigkeit und Bändermodell

	Das Ohmsche Gesetz ist nur sinnvoll für spezifische Größen:			j  =  s ·  E       s  =  1 /r
		j=Stromdichte
		E=Feldstärke .
		Wesentliche Materialkonstante ist: Leitfähigkeit s oder spez. Widerstand r.
	Typische Werte sind wichtig!			r (Metall)  »  1 µ Wcm       r (Halbleiter)  »  1 Wcm       r(Isolator)  »  1 GWcm
		Man muss mit den ca. 1 µWcm guter reiner Metalle (Ag, Cu) leben, man kann sie immer nur verschlechtern (Defekte , Legieren, ...), aber nie besser machen.
	Elektrische Stromdichte ist ein Nettostrom geladener Teilchen, gegeben durch Zahl der Ladungen=Teilchen, die pro Sekunde mit einer mittleren Nettogeschwindigkeit v D durch einen cm2 fließen.			j  =  q · n · vD s  :=  q · n · vD E  =  constant           vD E  =  m=constant   (Beweglichkeit) s  =  q · n · µ
		Das läßt sich immer so schreiben Þ
		Die Driftgeschwindigkeit vD, verursacht durch das elektrische Feld, ist aber extrem klein gegenüber der mittleren thermischen Geschwindigkeit vtherm
		Für die Leitfähigkeit ergibt sich sofort Þ
		Damit ist ein neuer, sehr wichtiger Materialparameter, die Beweglichkeit m definiert.
		Das Ohmsche Gesetz ist nun hergeleitet, in der "Materialform" schreibt es sich Þ
	Die Konzentrationen nMet der Ladungsträger in Metallen nMet und Isolatoren nIso sind von der Größenordnung her bekannt: Ungefähr Dichte Atome bzw um Null.			nMet » Atome            nIso  » 0
		Es bleibt, die Beweglichkeit m zu bestimmen
		Bei Halbleitern ist nHalb noch nicht klar, hier brauchen wir nHalb und mHalb.
	Eine relativ simple Betrachtung des Herumwuselns von Elektronen in Kristallen ergibt folgende Beziehungen:
		Stöße zwischen Elektronen und den den Haupstoßpartner "Phononen"=Träger der thermischen Energie=anderes Wort für (quantisierte) Gitterschwingungen und Kristallgitterdefekten (Fremdatomen, Korngrenzen, Versetzungen, Ausscheidungen, ...) sorgen für eine im Mittel konstante Driftgeschwindigkeit.
		Charakteristische Parameter dazu sind die (mittlere) Stoßzeit t und die mittlere freie Weglänge l=vt.
		Die Beweglichkeit ist dann direkt gegeben (d.h. proportional) zu l=vt oder t. (Formel muss man nicht wissen).
	Die Temperatur bestimmt klassisch sowohl v (über ½mv2=3/2 kBT) als auch (über Stöße mit "Phononen") zum Teil die Beweglichkeit.			Es kommt Unsinn raus! Pauli-Prinzip! Der Gleichverteilungssatz gilt nicht für Fermionen!
		Für eine gegebene Elektronenkonzentration (z. B. typisches Metall) und eine gemessene Leitfähigkeit kann man damit alle Größem ausrechnen, aber Þ
		Elektronen können nicht mit beliebigen Geschwindigkeiten=Energie=Zuständen existieren; sie können z. B. bei T=0 K nicht alle bewegungslos sein.
		Trotzdem behalten alle obigen Formeln außer ½mv 2=3/2 kBT auch in der nachfolgenden "richtigen" Betrachung ihre Bedeutung – wir müssen nur die Geschwindigkeit richtig bestimmen.
	Als Fermionen unterliegen die Elektronen der Fermiverteilung, und sie sind nicht völlig frei in der Wahl ihres Energiezustands, denn in einem kristallinen Festkörper sind sie quantenmechanisch als Elektronenwellen zu beschreiben.			Nur Elektronen im Aufweichungsbereich der Fermiverteilung sind "handlungsfähig"! Die Bandstruktur der Elektronen in einem Kristall bestimmt die elektronischen Eigenschaften!
		Aus der Fermiverteilung folgt eine fundamentale und weitreichende Eigenschaft der Elektronen: Þ
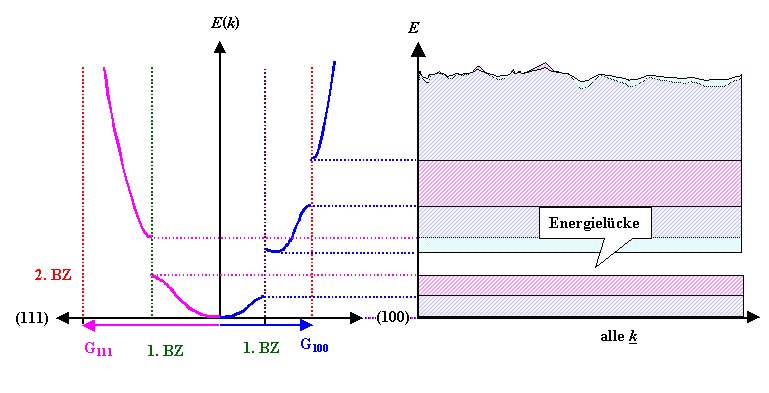
		Aus der quantenmechanischen Beschreibung als Elektronenwellen resultiert eine Bandstruktur E(k), welche den Zusammenhang zwischen der Energie E eines Elektrons und seinem Wellenvektor k angibt. Dabei kann es bestimmte Energiebereiche geben, zu denen kein einziger Wellenvektor paßt – wir haben es mit einer Bandlücke zu tun. Es gilt: Þ
		Die Bandstruktur E(k) kann auf die Zustandsdichte D(E) umgerechnet werden; Näheres dazu weiter unten. Die Bandlücken sind die Energiebereiche, in denen die Zustandsdichte gleich null ist.
		Wegen der Kompliziertheit der vollständigen Bandstruktur geht man zu einer stark vereinfachten Darstellung der Energien von Kristallelektronen über: Es wird nur noch betrachtet, welche Energiewerte erlaubt und welche verboten sind – und das ganz und gar unabhängig von der Richtung im reziproken Raum der k-Vektoren. Das Ergebnis ist dann ein Banddiagramm :
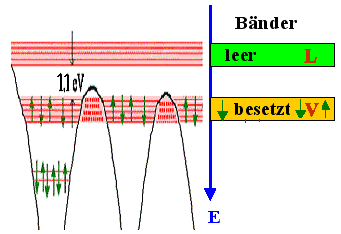
	Die allgemeinste Bandstruktur hat als bei großen Energien ein volles oder teilgefülltes Valenzband V, getrennt durch eine Energielücke EG vom (fast) leeren Leitungsband L (oder englisch C).
		Bänder oder Zustände unterhalb des Valenzbandes sind per definitionem immer voll besetzt und damit "tot" – nichts kann passieren.
		Bänder oder Zustände oberhalb des Leitungsbandes enthalten keine Elektronen und sind damit "tot" – nichts kann passieren
		Zwei Bänder genügen, mit der weiteren Abstraktion, daß EG=0 eV erlaubt ist.
		Wo immer dieElektronen sich befinden – nur in der Aufweichungszone um die Fermienenergie können sie "was tun".
	Die Bandstruktur bestimmt zunächst die Leitfähigkeit. Þ
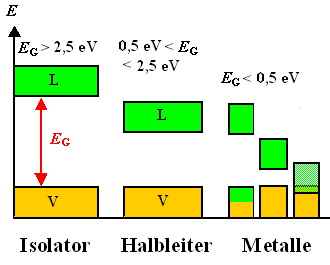
		Isolatoren: Große Bandlücke (EG ³ 2,5 eV. Valenzband komplttt voll Leitungsband komplett leer. es gibt keineLadungsträger, die "was tun" könnten.
		Leiter: (=Metalle). Bandlücke EG £ 0,5 eV, insbesondere aber =0 eV, oder Valenzband nicht voll gefüllt. Es gibt viele Elektronen an der "Fermikante", die beweglich sind (Bewegung=Zustand ändern=anderen Platz besetzen, der dazu frei sein muß).
		Halbleiter: Bandlücke 0,5 eV £ EG £ 2,5 eV. Bei endlicher Temperatur reicht die thermische Energie kBT, um hinreichend viele Elektronen ins Leitungsband zu werfen. Im Valenzband bleiben bewegliche pos. geladenen Löcher zurück.
	Zugehörige typische spezifische Widerstandswerte Þ			rAg  =  1,63 · 10– 6 Wcm=1,63 µWcm rHL  »   1 Wcm (»1000 – 0,001) Wcm rIso  ³ 109 Wcm =  1 GWcm
		rMet ist nicht "einstellbar". Defekte oder legieren machen r immer nur größer. rAg ist bei RT durch nichts zu unterbieten. Großes Problem für ET&IT!
		rHL ist in weiten Grenzen (mindestens 4 Größenordnungen) einstellbar durch Dotieren).

© H. Föll (MaWi für ET&IT - Script)