8.4.2 Was man wissen muss

	Wir verstehen, wie elektrischer Strom mit dem Netto-Teilchenströmen zusammenhängt, und dass nur Stromdichte j und elektr. Feldstärke E im Zusammenhang mit Materialien sinnvolle Größen darstellen.
	Wir verstehen das Ohmsche Gesetz in der nachfolgenden Form, und dass es implizit behauptet, dass die spez. Leitfähigkeit s = 1/r (r = spez. Widerstand) eine Materialkonstante ist.
		j  =  s · E  =  E r j  =  q · n · vD s  =  q · n · µ Ohmsches Gesetz Muss man wissen Stromdichte und Driftgeschwindigkeit geladener Teilchen Muss man nicht wissen, aber verstehen Materialdefinition der spez. Leitfähigkeit Muss man wissen
	Wir können s = q · n · µ erläutern:
		Die Ladungsträgerdichte n ist: n Met » Dichte der Atome für Metalle , nIso = 0 cm–3 für Isolatoren, nHL = Neff · exp[–(EL – EF)/(k BT)] cm–3 » NDot cm–3 für Halbleiter
		Bei Halbleitern ist dabei schon Wissen eingeflossen, das wir uns erst im nächsten Kapitel erarbeiten.
		Die Beweglichkeit µ bringt zum Ausdruck, dass die Driftgeschwindigkeit vD im elektrischen Feld trotz konstanter Kraft auf die Ladung konstant ist; es gilt µ = vD/E .
		Statt der klassisch dazu notwendigen Reibung haben wir Stöße der Ladungsträger (Elektronen oder Löcher) mit haupsächlich thermischen Gitterschwingungen (Phononen genannt) und Defekten wie atomaren Fehlstellen (insbesondere Fremdatome), Versetzungen, Korngrenzen etc.
		Die relevanten sinnvollen Größen in diesem Zusammenhang sind mittlere Stoßzeiten t und mittlere freie Weglängen l µ t µ µ. Die Beweglichkeit ist also schlicht ein Maß für die Stoßerei.

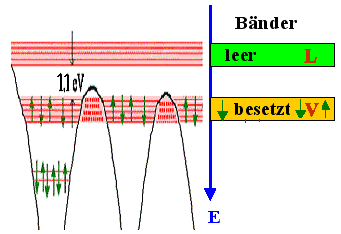
	Das folgende Bild können wir interpretieren:
					Stoßzeit und mittlere freie Weglänge sind klar.
					Was das elektrische Feld E macht, ist klar.
					Dass ohne Feld < v+x> = < v–x> >> vD und < v> = 0 cm/s, ist nicht nur klar, wir wissen sogar, wie man < vtherm > klassisch mit dem Gleichverteilungssatz ausrechnen kann, und warum man in den obigen Gleichungen höllisch aufpassen muss, ob da ein Vektor oder ein Skalar steht.
					Wir haben sogar ein Gefühl für Zahlen: vD liegt eher bei cm/s, während vtherm eher bei zigtausenden cm/s liegt (bei RT).

	Wenn wir die mittlere freie Weglänge ausrechnen (mit gemessenen s-Werten), wird uns klar, dass Elektronen sich nicht mal ungefähr als klassische Teilchen verhalten (mittlere freie Weglängen wären viel zu klein), und warum sie noch viel schneller sein müssen, als aus dem klassischen Gleichverteilungssatz (½mv 2 = 3/2 kBT) errechnet.
		Wir können das im Umfeld der Begriffe " Pauli-Prinzip", "Zustände " und "Besetzung von Zuständen" erläutern und die Problematik aufzeigen, insbesondere bei sehr tiefen Temperaturen.
	Wir verstehen, dass alle gelernten Begriffe trotzdem ihre Bedeutung behalten: Dass die "Hintergrundgeschwindigkeit" vtherm nicht "stimmt", ist für die Hauptformel s = q · n · µ egal, sofern n = Konzentration der beweglichen Ladungsträger bedeutet.
		Damit haben wir Metalle und Isolatoren "erledigt" und insbesondere verstanden, dass man an nMet nicht nenneswert "drehen" kann, dass die Beweglichkeit immer mit zunehmder Temperatur runtergeht (und dass man dagegen nichts tun kann), und dass alle üblichen Tricks (Defekte, Legieren, ...) die Beweglichkeit und damit s immer nur schlechter machen.
		Wir kennen typische Zahlen (für r ): r (Metall) » 1 µWcm. r (Halbleiter, dotiert) »1 Wcm. r (Isolator) >> 1 Wcm.
	Es bleiben "nur" noch die Halbleiter.
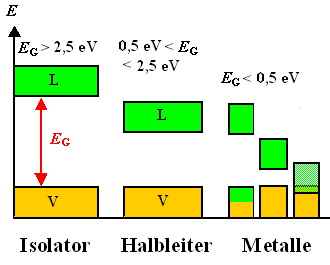
		Wir haben uns überzeugt, dass wir Halbleiter (und den Rest auch nochmal) sinnvollerweise über das Bändermodell angehen, die beiden nachfolgenden Bilder können wir sofort verstehen und ggf. im Detail erläutern:
	Der Begriff der Zustandsdichte ist uns halbwegs klar (und nach dem nächsten Kapitel vollständig klar), und wir können im Schlaf folgenden Spruch aufsagen:
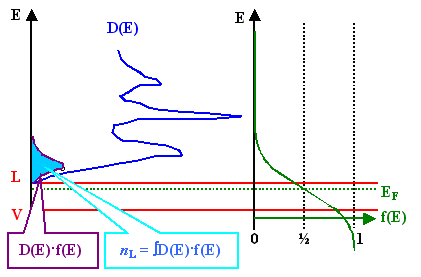
		Dichte der Elektronen bei Energie E = Zahl der vorhandenen Plätze (= Zustandsdichte D(E)) mal Wahrscheinlichkeit der Besetzung (= f(E) = Wert der Fermiverteilung bei E). Gesamtzahl durch Aufsummieren = Integrieren.
		Wir können das zur Not auch in Formeln hinschreiben (inkl. der blauen, die wir aber erst in den nächsten Kapiteln lernen )
		neL(T)   =  ¥ ó õ EL D(E) · f(E; EF,T) dE           =  Neff · exp[–(EL – EF)/(kBT)]         £ NDot    für Majoritäten nMin   =  ni 2 nMaj           =  ni2 NDot
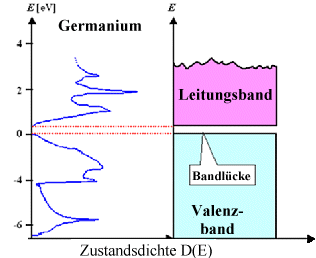
	Wir wissen auch schon, dass Zustandsdichten zwar nicht so leicht zu rechnen sind, aber letztlich bekannte Materialparameter (in Form einer Kurve) darstellen. Das nachfolgende Germanium-Bild ist uns klar.
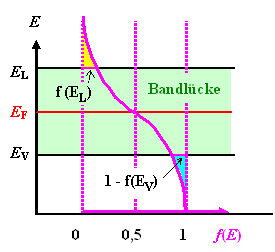
		Wir könnten sogar mit den beiden nachfolgenden oberen Bildern das untere Bild qualitativ konstruieren und mit obiger Formel begründen.
		Wir könnten das Ganze auch für Löcher (= unbesetzte Plätze im Valenzband) machen, und wir sind uns über die Bedeutung von 1 – f(E) in diesem Zusammnhang im Klaren.
	Wir wissen aber auch, wie man sich mit effektiven Zustandsdichten (ein Materialparameter in Form einer Zahl ) und der Boltzmann-Näherung für f(E) das Leben stark vereinfachen kann, und wir haben die folgenden Formeln verinnerlicht und immer parat:
		neL( T)  =  Neff · exp[–(EL – EF)/(kBT)] nh V(T)  =  Neff · exp[–(EF – EV)/(kBT)] Þ      ne ·nh  =  ni2 Dichte der Elektronen im Leitungsband Dichte der Löcher im Valenzband Massenwirkungsgesetz
	Es ist uns klar, dass das Massenwirkungsgesetz rechts außen aus den beiden Formel links unmittelbar folgt; wir verzeihen auch dem Menschen, der den blöden Namen geprägt hat.
		Nebenbei haben wir uns an das Konzept der Löcher gewöhnt.

© H. Föll (MaWi für ET&IT - Script)