|
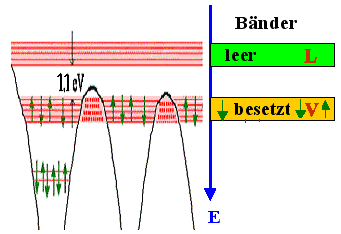
Die allgemeinste Bandstruktur hat als bei großen Energien ein volles oder
teilgefülltes Valenzband
V, getrennt durch eine Energielücke EG
vom (fast) leeren Leitungsband L (oder englisch C). |
|
|
|
 |
Bänder oder Zustände unterhalb des Valenzbandes sind per definitionem
immer voll besetzt und damit "tot" – nichts kann passieren. |
|
|
 |
Bänder oder Zustände oberhalb des Leitungsbandes enthalten keine Elektronen und
sind damit "tot" - nichts kann passieren | |
|
 |
Zwei Bänder genügen, mit der weiteren Abstraktion, dass EG=0
eV erlaubt ist. | |
|
 |
Wo immer dieElektronen sich befinden - nur in der Aufweichungszone um die Fermienenergie können
sie "was tun". | |
| |
| |
|
 |
Die Bandstruktur bestimmt zunächst die Leitfähigkeit. Þ
| |
|
|
 |
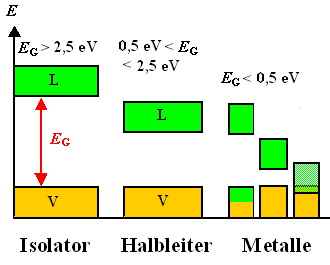
Isolatoren: Große Bandlücke (EG
³ 2,5 eV. Valenzband komplettt voll, Leitungsband komplett leer. Es gibt keine Ladungsträger,
die "was tun" könnten. | |
|
 |
Leiter: (=Metalle). Bandlücke EG
£ 0,5 eV, insbesondere aber =0 eV, oder Valenzband nicht voll gefüllt. Es
gibt viele Elektronen an der "Fermikante", die beweglich sind (Bewegung=Zustand ändern=anderen Platz besetzen,
der dazu frei sein muss). | |
|
 |
Halbleiter: Bandlücke 0,5 eV £
EG
£ 2,5 eV. Bei endlicher Temperatur reicht die thermische Energie kBT
um hinreichend viele Elektronen ins Leitungsband zu werfen. Im Valenzband bleiben bewegliche pos. geladenen Löcher
zurück. | |
| | |
| |
|
 |
Zugehörige typische Leitfähigkeiten Þ |
|
| r
Ag = 1,63 · 10–6Wcm |
| rHL » 1 Wcm
|
| rIso ³ 1 GWcm
|
|
|
 |
rMetist nicht "einstellbar". Defekte
oder legieren machen r immer nur größer. rAg
ist bei RT durch nichts zu unterbieten. Großes Problem für ET&IT! |
|
|
 |
rHL ist in weiten Grenzen (mindestens 4
Größenorndungen) einstellbar durch Dotieren ). |
|
| |
| |
 |
Hier ist noch was zu tun: | |
|
|
 |
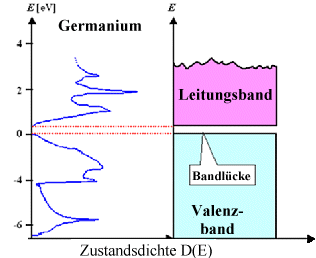
Dichte der Elektronen bei E=Zahl der vorhandenen Plätze
(=Zustandsdichte D(E)) mal Wahrscheinlichkeit der Besetzung (=f(E)=Wert der Fermiverteilung
bei E): Gesamtzahl durch Aufsummieren=Integrieren. |
|
|
 |
Zustandsdichten sind komplizierte Funktionen aber trotzdem
"nur" Materialkonstanten. |
|
|
 |
Vereinfachung durch effektive Zustandsdichten
Neff (Zahl statt Kurve) und Boltzmann-Näherung
der Fermiverteilung. | |
|
 |
Dichte der Löcher über Wahrscheinlichkeit für Nichtbesetzung=1 – f(E). |
|
| |
| |
| |
© H. Föll (MaWi für ET&IT - Script)