7.3 Technische Nutzung des Ferromagnetismus

7.3.1 Hart- und weichmagnetische Materialien

Definitionen

	Schauen wir uns schnell die im vorhergehenden Modul aufgeworfenen Fragen an:
		1. Was für eine optimale Hysteresekurve brauche ich überhaupt für die geplante Anwendung?
	Wir nehmen mal die zwei Hauptanwendungsbereiche: Transformatorkern und magnetischer Speicher.
		Der Transformatorkern muss ferromagnetisch sein, um einen möglichst großen magnetischen Fluss B von der Primärspule zur Sekundärspule transportieren zu können. Was man möchte ist, dass der induzierte Fluss B dem Primärfeld H so perfekt wie möglich folgt.
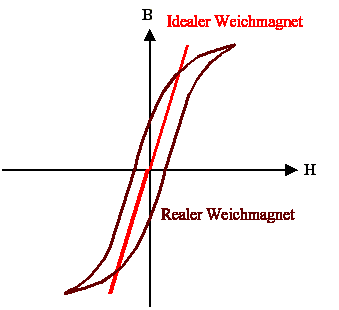
		In anderen Worten: Wir brauchen ein Material mit möglichst gar keiner Hysterese – B(H) sollte eine möglichst gerade Linie sein, wie unten gezeigt.
				Eine ideale, hysteresefreie Magnetisierungskurve gibt es in technisch relevanten Matierialien jedoch nicht. Was wir haben sind allenfalls Weichmagnete mit sehr schlanker Hysterese und damit kleinen Werten für Koerzitivkraft und Remanenz
				Hystereseverluste sind jetzt klein, aber nicht ganz vermeidbar.
				Die Energieerzeugungsindustrie wäre glücklich, wenn die vorhandenen (Fe-basierten) Materialien noch 1 % oder 2 % "weicher" gemacht werden könnten. 1 % weniger Verluste bei 100 MW ist auch schon was.
				Neben Hystereseverluste hat man noch ein zweites Problem: Jede Abweichung der Magnetisierungskurve von einer perfekten Geraden bedeutet, dass das Ausgangssignal gegenüber dem Eingangssignal etwas verzerrt ist. Gibt man einen sin(wt) rein, kommen auch höhere Harmonische - sin(nwt) mit entsprechend kleiner Amplitude mit raus.
	Ein weichmagnetisches Material wird für einen Permanentmagnet ungeeignet sein, weil seine bleibende Magnetisierung – die Remanenz – klein ist.
		Für magnetische Speicherung von Bits brauchen wir aber einen Permanentmagneten. Denn wir speichern Daten, indem wir mit einem "Schreibkopf" in einem magnetischen Material auf Band oder Scheibe eine permante Magnetisierung bei einer bestimmten Koordinate einprägen. Diese Magnetisierung sollte für viele Jahre unverändert bleiben.
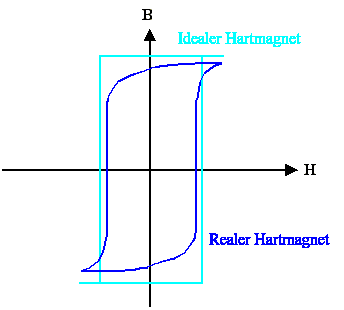
		Das magnetische Bit muss also stark genug sein – auch wenn es nur eine winzige Fläche in Anspruch nimmt – um nicht bei kleinsten Störungen zufällig gelöscht zu werden, und um im "Lesekopf" ein kräftiges Signal zu erzeugen. Es soll aber auch nicht zu stark sein, denn das macht das Löschen und Schreiben zu aufwendig. Das Material sollte damit die folgende Hysteresekurve haben:
				Die Hysteresekurve sollte so rechteckig als möglich sein, Koerzitivkraft und Remanenz haben genau definierte Werte. Wir brauchen einen Hartmagneten.
				Die Magetisierung ändert sich oberhalb eines bestimmten Feldes kaum mehr.
				Wir die Feldrichtung umgedreht, ändert sich erst kaum was, dann klappt die Magnetisierung ziemlich plötzlich um.
				Hystereseverluste sind unvermeidlich. Es steckt sogar ein viel tieferes Prinzip in dieser Bemerkung: Information unterliegt der Thermodynamik, es gibt sie energetisch (und entropisch) nie "umsonst". Schreiben und Lesen "kostet" Energie.
	So gut wie alle Anwendungen magnetischer Materialien brauchen entweder Hart- oder Weichmagnete. Damit werden Antworten auf die 2. und 3. Frage des vorherigen Moduls jetzt relevant

	Hysteresekurven manipulieren
	Zunächst müssen wir ein Grundmaterial selektieren. Dafür haben wir reiche Auswahl:
		Wir können zwischen den drei ferromagnetischen Elementen Fe, Ni, Co wählen oder anfangen, diese Metalle zu legieren.
		Dann können wir Verbindungen mit fast-magnetishen Elementen wie Cr, Mn, oder O machen, um schließlich bei "Exoten" zu landen. Der Link zeigt was im Umfeld von Permanentmagneten so läuft.
	Dazu machen wir noch schnell eine kleine Aufgabe:
		Übungsaufgabe Aufgabe 7.3-1
	Das Feld ist zu groß und zu komplex um hier noch tiefer einsteigen zu können. Schauen wir deshalb noch schnell auf die Frage: Kann ich bei gegebenem Material die Hystereskurve anpassen?
		Die Antwort ist:ja. Immer in Grenzen, natürlich.
		Warum und wie? Nun, Hysteresekurven beschreiben immer auch wie leicht oder schwer es ist, Domänenwände zu verschieben. Da Domänenwände an Defekten gepinnt werden können, ist das eine Funktion der internen Defektstruktur – und die kann ich ändern.
	Schauen wir uns einfach ein paar Beispiel an:.
				Zwischen "ausgeheiltem" Eisen, d. h. Eisen mit wenigen Versetzungen und großen Körnern, und stark verformten Eisen mit kleinen Körnern und hohen Versetzungsdichten, besteht bezüglich der Hysteresekurven ein großer Unterschied.
				Offenbar ist die Bewegung der Domänenwände im stark verformten Eisen sehr viel schwieriger, wie das auch zu erwarten war.
				Das wird in allen anderen Materialien ähnlich sein müssen. Statt zu verformen können wir auch atomare Fehlstellen ("Dreck") einbringen, kleine Ausscheidungen machen, .... Allerdings machen wir damit das Material immer nur "härter".

	Wir können das Material auch nur mal unter mechanische Spannung setzen, d.h. die Atomabstände durch Ziehen oder Drücken in einer Richtung etwas ändern. Da die Wechselwirkung zwischen den magnetischen Momente der Atome, die die Ausrichtung erzwingt, sehr stark vom Abstand abhängt, sollte etwas passieren:
		Die Effekte sind in der Tat bemerkenswert, besonders im Nickel:
		In diesem Fall ist die Dehnung parallel zum externen Feld H		In diesem Fall ist die Dehnung im rechten Winkel zum externen Feld H
		Wir finden eine große Absenkung der Remanenz, aber keine großen Unterschiede bei der Koerzitivfeldstärke .		Wiederum keine großen Unterschiede bei der Koerzitivfeldstärke, aber eine große Anhebung der Remanenz. Wir haben ideales hartmagnetisches Verhalten.
	Das letzte Wort zum Thema:
		Die Zukunft des "Magnetismus" sieht gut aus. Mit zunehmendem Verständnis für die Grundlagen, gekoppelt mit Mikro- und Nanotechniken, werden viele neuartige Produkte möglich werden.
		Fragebogen Schnelle Fragen zu 7.3.1

© H. Föll (MaWi für ET&IT - Script)