|
Wir kennen die Begriffe "Feldstärke"
und "Stromdichte"; außerdem haben wir ein Gefühl für die Größenordnung
der Höchstwerte und Klarheit darüber, dass ein Dielektrikum nur Feldstärke "spürt", nicht
Spannung. Wir wissen, was e
r (oder "DK") bedeutet, zumindest in einem Plattenkondensator. |
 |
Wir kennen die Bedeutung der Dielektrika –
von Isolierungen über Kondensatoren bis zur Optik. Dazu gehört die Grundgleichung für den Brechungsindex
n2 = er. |
|
 |
Als Besonderheiten kennen wir noch den Zusammenhang zwischen Dielektrika und der die "Mikrowelle
" sowie Spezialtäten wie piezoelektrische Materialien. |
 |
Wir kennen die grunsätzlichen Antworten zu den drei Hauptfragen: |
| |
- Wie groß ist die Durchschlagsfestigkeit und durch was wird sie bestimmt? Þ
(0,1 . . . 10) MV/cm. Es gibt mehrere Mechanismen, z.B. Lawinendurchbruch.
- Was bestimmt e r? Þ
Polarisationsmechanismen
: Grenzflächen-, Orientierungs-, Ionen- und Elektronenpolarisation (letztere = Atompolarisation).
- Was bestimmt die Frequenzabhängigkeit von er(w)? Þ Resonanz oder Relaxation.
|
 |
Wir kennen und verstehen die Grundgleichungen: |
|
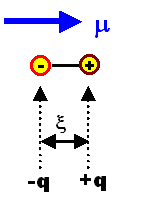
Elektrisches Dipolmoment
(x ist der Abstands-
vektor von der
negativen zur
positiven Ladung;
in der Skizze
rechts ist |x| gezeigt) |
|
 | | Polarisation des Materials |
| Sinnvolles
Materialgesetz |
| Sinnvolle neue
Materialkonstante |
| Alte
Materialkonstante |
| | Beziehung D Û
P |
|
|
|
 |
Wir wissen, welche Materialien intrinsische elektrische Dipole haben und welche
nicht. Wir können das z. B. für Wasser und NaCl auch skizzieren – inkl. der Polarisation mit und
ohne Feld. |
 |
Das Ersatzschaltbild eines idealen und realen Dielektrikum (für DC
oder kleine Frequenzen) ist bekannt, wir können den (Verschiebungs-)Strom hinschreiben und begründen, warum das
auf eine komplexe DK
e = e' – ie '' führt. |
|
 |
Wir verstehen insbesondere, warum der Imaginärteil
–e'' die Wirkleistung beschreibt und damit
die dielektrischen Verluste. |
 |
Soweit die drei Hauptmechanismen der Polaristion betroffen sind, wissen wir: |
|
 |
Bei der Atom- bzw. Elektronenpolarisation verschiebt
das elektrische Feld die Ladungsschwerpunkte der Elektronenhülle relativ zum Atomkern. Der Effekt ist sehr schwach
für Kugelsymmetrie (z. B. Edelgasatome; e
» 1), aber stark für gerichtete Bindungen (z. B. Si und andere Halbleiter:
e » 10 . . . 20). |
|
 |
Bei der Orientierungspolarisation
drehen
sich vorhandene Dipole etwas in Feldrichtung; damit kann sie nur bei Flüssigkeiten
autreten. Orientierungspolarisation verursacht e
» 80 bei Wasser (und steckt hinter dem Wirkprinzip der "Mikrowelle"). |
|
 |
Bei der Ionenpolarisation werden die vorhandenen Dipole
in polaren Kristallen abwechselnd etwas kleiner oder größer, der Nettoeffekt verursacht die DK. |
 |
Die Frequenzabhängigkeit der DK resultiert aus der Tatsache, dass
bei jedem Polarisationsmechanismus Massen bewegt werden müssen, um Polarisation
zu erzeugen, und das geht nicht beliebig schnell. |
|
 |
Wir kennen die 2 relevanten Mechanismem: Resonanz
und Relaxation. Wir können sie den drei Polarisationsmechanismen zuordnen |
 |
Wir können die komplette Bewegungsgleichung für Resonanz hinschreiben
und diskutieren. Wir kennen insbesondere die Formel für die Resonanzfrequenz
w0 (ohne Dämpfung): |
| |
| m · |
d2x
dt2 |
+ kR · m · |
dx
dt |
+ kF · x |
= |
q · E0 · cos(wt) |
| w0 | = |
æ
ç
è |
kF
m |
ö
÷
ø | 1/2 |
|
|
|
 |
Wir wissen insbesondere auch, dass die Federkonstante k F direkt
mit dem Elastiztitätsmodul Y (oder E)
verknüpft ist (k Fed = E · r0 mit r0
= Bindungsabstand oder ungefähr "Gitterkonstante" a) und damit dielektrische Eigenschaften
mit mechanischen verknüpft sind. |
|
 |
Damit wissen wir, dass Resonanz
bei der ionischen Polarisation um 1013 Hz auftritt; bei der Elektronenpolarisation liegt sie um 1015
Hz, also im optischen Teil des Spektrums. |
|
 |
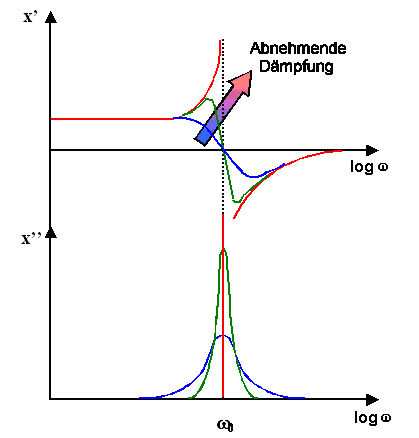
Wir wssen, warum die resonanten Mechanismen in Kristallen stark gedämpft
sind, und wir können das Prinzipbild für die komplexe Amplitude nach Real-
und Imaginärteil getrennt skizzieren: |
|
|
|
 |
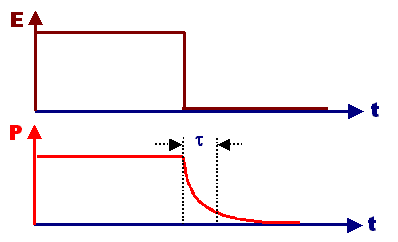
Der Mechanismus der Relaxation gehört
zur Orientierungspolarisation. Nach Abschalten des elektrischen Felds haben die etwas
ins Feld orientierten Dipole zu viel freie Energie (da zu wenig Entropie); wir beobachten das generelle Verhalten des Zerfalls
angeregter Zustände. |
|
 |
Wir wissen, wie das aussieht und wie die generelle Formel dazu lautet: |
| |
|
|
 |
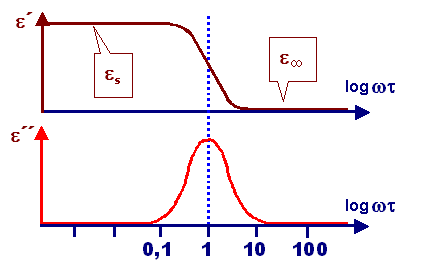
Wir wissen, wie man von einer Zeitfunktion per Fouriertransformation zu einer Frequenzfunktion
kommt; wir müssen aber nicht wissen, wie das exakt geht. Allerdings kennen wir
das Ergebnis in graphischer Form: |
|
|
|
 |
Damit können wir:
- den Real- und Imaginärteil der dielektrischen Funktion für ein fiktives Material, in dem alle
Mechanismen vorliegen, qualitativ zeichen und die wichtigen Frequenzen in ungefähren
Zahlen den diversen Prozessen und Polarisationsmechanismen zuordnen;
- begründen, warum es so ein Material nicht geben kann;
- die Polarisationsmechanismen und ihre Frequenzabhängigkeit etwas detaillierter erläutern.
|

|
Soweit die Optik betroffen ist, wissen wir,
wo sie in der ET&IT eine große Role spielt: optische Kommunikation (Laser, Glasfaser, Photodioden, ...),
LEDs, Displays, Solarzellen, ... |
|
 |
Der Zusammenhang mit Dielektrika ergibt sich aus der schlichten Formel: (komplexer Brechungsindex)2
= dielektrische Funktion. |
|
 |
Wir können die grundsätzliche Fragestellung der Optik skizzieren und mit Real- und
Imaginärteil des komplexen Brechungsindex verbinden. |
 |
Þ In der (komplexen) dielektrischen Funktion eines Materials stecken alle elektrischen
und optischen Eigenschaften des Materials. |
 |
Falls wir wirklich gut sind, können wir noch folgende Begriffe plus wichtige
Anwendungen erläutern: - Piezoelektrische Materialien.
- Ferroelektrische Materialien.
- Elektrete.
- Pyroelektrizität.
|
| |
|
© H. Föll (MaWi für ET&IT - Script)