|
Spannung und Strom
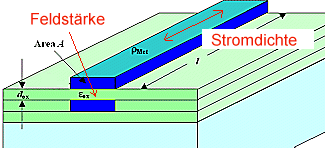
sind aus Materialsicht bedeutungslos, was zählt ist Feldstärke
E und Stromdichte j. |
|
|
|
 |
In Dielektrika=Isolatoren fällt die
Spannung ab. Das Dielektrikum wird durch das elektrische Feld polarisiert. |
|
|
 |
Dielektrika werden gebraucht für.
- Generelle Isolierung - von nm dicken "Gateoxiden" in IC's zu cm
dicken Hochspannungsisolatoren.
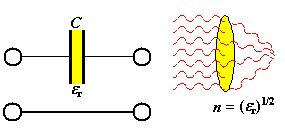
- Kondensatoren
- nicht nur als Bauelemetne sodern auch in unerwünschten parasitären
Kapazitäten.
- Kritischer Teil von MOS Transistoren .
- Wärmen mit Mikrowellen
- Als Piezomaterialien und Elektrete für
viele Anwenungen.
- Als optische Materialien ("Linse" bis Glasfaser und Laser).
| |
 |
Der Brechungsindex
n als bestimmende Kenngröße der Optik ist direkt mit der (relativen) Dielektrizitätskonstanten
er verknüpft. |
|
|
|
 |
Der DC-Wert der Dielektrizitäts"konstanten" für Wasser ist e
r(H2O) » 80; der Brechungsindex von Wasser ist n(H2O)
» 1,3. Der größtmögliche Brechungsindex liegt um nmax » 2,4 (Diamant). |
|
|
 |
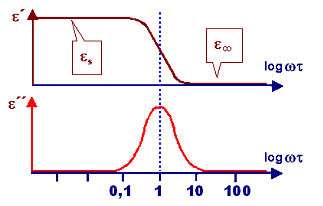
Þ e
r=er(w).
Die Dielektrizitäts"konstante"
ist frequenzabhängig
und wird tendenziell mit wachsender Frequenz kleiner. |
|
|
| |
| |
 |
Es sind drei Fragen zu beantworten |
|
- Was bestmmt die kritische Feldstärke Ekrit eines Dielektrikums?
- Was bestimmt er, die "DK"
- Warum und wie ist die DK frequenzabhängig?
|
|
|
 |
Nicht einfach. | |
|
 |
Aber machbar. | |
| | |
| |
|
 |
Ideale Dielektrika sind perfekte
Isolatoren charakterisiert durch ihre DK er oder durch die Suszeptibilität
c | |
Sinnvolles
Materialgesetz |
| Sinnvolle neue
Materialkonstante |
| Alte
Materialkonstante
(DK oder Permittivität) |
| Beziehung
D
Û P |
|
|
|
 |
Die DK oder die Suszeptibilität eines Dielektrikums folgt aus seiner
Polarisation. | |
|
 |
Die Beziehung zwischen Feld E und Polarisation
P ist aus Materialsicht sinnvoller als die Beziehung zwischen Feld und Verschiebungsdichte D |
|
|
 |
Umrechnungen sind einfach Þ |
|
| |
| |
| |
 |
Reale Dielektrika haben eine endliche Leifähigkeit |
|
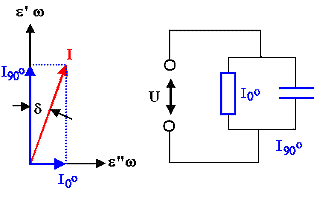 |
| j(w) | = |
w · e'' · E(w)
| + |
i · w · e' ·
E(w ) |
|
|
|
 |
Das läßt sich am einfachsten wie gezeigt beschreiben. Der insgesamt fließende
Wechselstrom wird durch eine komplexe dielektrische Funktion e(w)
erfaßt Þ | |
|
 |
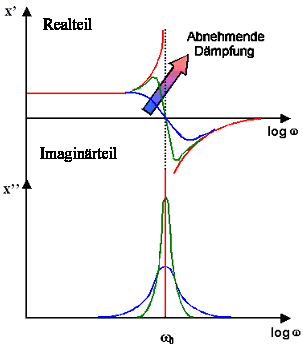
Der Realteil e' beschreibt den um 90o
phasenverschobenen Teil der Stromdichte j(w) und der Imaginärteil – e'' den Teil, der in Phase fließt. |
|
|
 |
Damit sind Wirk- und Blindleistung proportional zu e'' bzw.
e'. | |
|
 |
Dies gilt unabhängig davon von welchem Effekt der Imaginärteil resultiert. |
|
|
| |
| |
 |
Ein externes elektrisches Feld wird in einem Dielektrikum immer
Dipole induzieren und zusätzlich die eventuell vorhandenen Dipole verändern. |
|
|
|
 |
Die Polarisation eines Dielektrikum ist die Vektorsumme der enthaltene Dipolmomente per Volumen |
|
 |
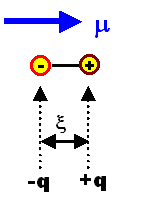
Ein Dipolmoment ist definiert wie gezeigt Þ |
|
| |
| |
|
 |
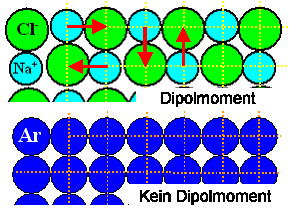
Viele Materialien enthalten Dipomomente (z. B. Ionenkristalle Oxide, Wasser, ...)
andere (Edelgas, dielektrische Elementkristalle) sind neutral |
|
|
|
 |
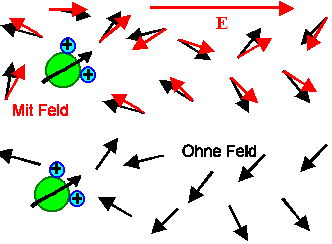
Im ersten Fall addieren sich die vorhandenen Moment ohne Feld i.d.R. zu P=0
C/cm2 ; mit Feld wird die Ausrichtung so geändert, dass P
¹ 0 C/cm2 resultiert. |
|
| |
| |
| |
 |
Es gibt neben der mathematisch schwer greifbaren Grenzflächenpolarisation
drei wesentliche Polarisationsmechanismen. |
|
- Atom- oder Elektronenpolarisation
- Ionenpolarisation
- Orientierungspolarisation
|
|
|
 |
Im 1. Fall wird die durch das Feld die Elektronenhülle relativ zum
Atomkern verschoben und dadurch ein Dipolmoment induziert.
- Sehr schwacher Effekt bei kugelförmigen Atomen (Beispiel Edelgase; auch als Kristall); er=1,00...
)
- Starker Effekt bei gerichteten kovalenten Bindungen (Beispiel typische Halbleiter Si, Ge, GaAs,
...); er=10 - 20.
|
|
|
 |
Die Ionenpolarisation ist in allen Ionenkristallen und
polaren Bindungen (Oxide, Keramiken) vorhanden. Mittel bis sehr stark. |
|
|
 |
Orientierungspolarisation kommt nur bei Flüssigkeiten
vor, da die (Molekül-)Dipole sich drehen können müssen. Recht stark: er(H2O)=80. |
|
| |
| |
| |
 |
In allen Fällen ist die Polarisation proportional
zum Feld. | |
|
|
 |
Damit ist die Grundgleichung "bewiesen"; die Suszeptibität
c kann berechnet werden. | |
| | |
| |
 |
Frequenzabhängigkeit der Polarsation.
Uns interssieren Frequenzen bis in Ultraviolette - d. h. jenseits 1015 Hz |
|
|
|
 |
Die Grundbeziehung ist Þ |
|
|
 |
Wie Eingang und Ausgang aussieht, hängt von der Frequenz ab. |
|
|
 |
Bei optischen Frequenzen wird man z. B. Licht durch eine Linse schicken, bei RF reicht es, einen Kondensator
zu vermessen. | |
|
| |
| |
 |
Es gibt nur zwei grundlegende Mechanismen,
die die Frequenzabhängigkeit der DK bestimmen:
|
|
|
|
 |
Elektronenpolarisation und ionische Polarisation zeigen Resonanz,
die Orientierungspolarisation zeigt Relaxation. |
|
| |
| |
| |
 |
Resonanz erhält man beim getriebenen gedämpften Schwinger. |
|
| m · |
d2x
dt2 |
+ mkR · |
d x
d t |
+ kF · x |
= |
q · E0 · cos(wt) |
|
|
|
 |
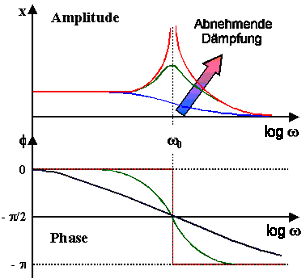
Die Lösungen kann man als Amplitude und Phase oder als Real- und Imaginärteil einer
komplexen Amplitude darstellen. | |
|
 |
Die Amplitude bestimmt das elektrische Dipolmoment, da in beiden Resonanzmechanismen die Ladungen
gegeneinander schwingen. | |
| | |
| |
|
 |
Die Lösungen der Differentialgleichung kann man für Amplitude und Phase
angeben (unten) oder für Real- und Imaginärteil (rechts). Wir nehmen natürlich die komplexe Variante! |
|
|
| |
| |
| |
| |
| |
| |
|
|
 |
Damit ist der Verlauf der komplexen DK im Bereich der Resonanzen grundsätzlich
skizziert. | |
|
| |
| |
 |
In allen Materialien muss die Resonanz stets stark gedämpft sein, da die
die Energie eines heftig schwingenden Dipols sofort auf Nachbarn dissipiert wird. |
| |
| | |
| |
 |
Die Resonanzfrequenz w0 ist gegeben
durch Þ | |
| w0 | = |
æ
ç
è |
kF
m |
ö
÷
ø | 1/2 |
|
|
|
 |
In der Federkonstante der ionischen Polarisation steckt der E-Modul. Es schwingen
"schwere" Atome, und wir wissen schon, dass
w0
» 1013 | |
|
 |
Bei der Atom- oder Elektronenpolarisation schwingen leichte Elektronen, daher
w0
» 1015
d.h. die Resonanz liegt im optischen Bereich. |
|
| |
| |
| |
 |
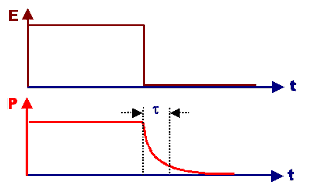
Die Relaxation, d.h. allmähliche Rückkehr
aus dem etwas orientierten Zustand nach Abschalten des Felds in den völlig ungeordneten Zustand, wird beschrieben durch
Þ | |
|
|
 |
Aus der Grundgleichung in der Zeit |
|
|
| |
|
|
|
| P(t) | = |
P0 · exp ( – | t
t | ) |
|
| |
|
| |
| |
|
 |
folgt durch Fourier-Transformation die Grundgleichung in der Frequenz.
Der Graph dazu
sieht so aus Þ | |
|
|
 |
Der Wert der typischen Relaxationszeitkonstanten tliegt
im Bereich 1/t » 10 GHz |
|
|
 |
Insbesondere der Imaginärteil erklärt die Funktionsweise der "Mikrowelle
" | |
| | |
| |
|
 |
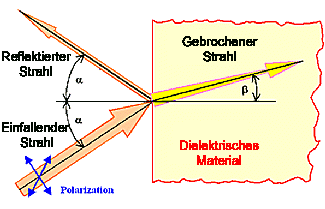
Optik und Dielektrika. Licht fällt auf
ein (dielektrisches) Material | |
|
|
 |
"Input" Größen sind die Frequenz
(Größenordnung 5 · 1014 Hz), die Intensität
I0, der Einfallswinkel und die Polarisationsebene
. | |
|
 |
Alles was passieren kann ist: - Brechung
, d. h. Eindringen in das Material mit Intensität IM unter dem Winkel b
- Reflexion mit Intensität R=I0 – IM.
- Absorption mit IM(z)= IM(z=0)
· exp(–az); 1/a ist die Absorptionslänge
| |
|
| |
| |
 |
Die dielektrische Funktion des Materials enthält die die gesamte notwendige
Information | |
| (n + ik)2 | = |
e ' – i · e'' |
| Blindleistung: | LB | = |
w · e' · E2
|
| Wirkleistung: | LW | = |
w · e'' · E2 |
|
|
|
 |
Dazu führt man einen komplexen Brechungsindex
ein Þ | |
|
 |
Im Realteil
n steckt die Information zu den Punkten 1 und 2. |
|
|
 |
Im Imaginärteil
k steckt die Information über die Absorption. |
|
| |
| |
| |
 |
Optik ist damit zurückgeführt auf
die Polarisation von Dielektrika bei hohen Frequenzen. | |
|
 |
Þ In der (komplexen) dielektrischen Funktion eines Materials stecken alle elektrischen
und optischen Eigenschaften des Materials. | |
|
© H. Föll (MaWi für ET&IT - Script)