5.2.3 Quantitative Berechnung der Fermienergie bei dotierten Halbleitern

Wo liegt die Fermienenergie - Dritter Teil

	Wir lassen beliebige Konzentrationen an Akzeptoren und Donatoren zu; betrachten aber nur zwei zusätzliche Niveaus in der Bandlücke bei ED und EA
		Die zugehörigen Zustandsdichten sind identisch mit den Konzentrationen der Dotieratome, d.h. wir haben ND und NA Plätze für Elektronen bei den zugehörigen Energien.
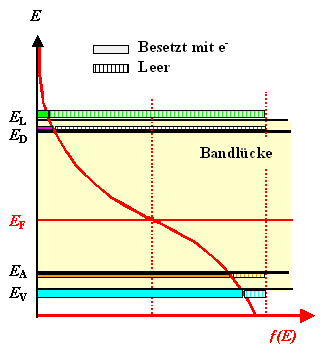
		Wir zeichnen das alles einfach mal in ein Banddiagramm und schauen uns an, wieviele der angebotenen Plätze besetzt sind bei einer Fermiverteilung mit zunächst noch willkürlich gewählter Fermienergie. Das ist jetzt einfach zu machen und schaut so aus:
		Die farbigen Balken symbolisieren (von oben nach unten) die Zustandsdichten
		NeffL   bei EL       ND   bei ED       NA   bei EA       NeffV   bei EV
	Was wir jetzt zu beachten haben, um die Fermienergie bestimmen zu können, ist Elektroneutralität - nur mit der Gleichsetzung zweier Konzentrationen wie bisher kommt man nicht weiter.
		Was für Ladungen haben wir zu beachten? Wo hat sich etwas geändert (immer im Vergleich zu T = 0K)?
		Schauen wir uns also die Bilanz an, getrennt nach negativen und positiven Ladungen. Wir schreiben das Ganze in fast voller Allgemeinheit mit der Fermiverteilung, nur die effektiven Zustandsdichten lassen wir zu um die unhandliche Integrale zu vermeiden.
		Negativ Positiv Art Formel Art Formel Elektronen in L nL = NeffL · f(EL , EF , T) Löcher in V nV = NeffV · {1 – f(EV , EF , T)} negativ ionisierte Akzeptoren N–A = NAL · f(EA , EF , T) positiv ionisierte Donatoren N+D = ND · {1 – f(ED , EF , T)}
		Alles was wir nun zu tun haben, ist Ladungsneutralität in der Form S neg. Ladungen = S pos. Ladungen aufzuschreiben, d.h. folgende Gleichung:
		NeffL · f(EL , EF , T) + NA · f(EA , EF , T)  =  NeffV · {1 – f(EV , EF , TV)} + ND · {1 – f(ED , EF , T)}
	Voilá - eine Gleichung für die eine Unbekannte EF - das hatten wir schon mal. Wir müssen nur nach EF auflösen - fertig!
		Ob man diese Gleichung wohl analytisch lösen kann? Nun - vergiß es!
		Es geht nicht; und wir müssen nun zu Fallunterscheidungen und Näherungen Zuflucht nehmen - oder zum PC, den wir ja zur Betrachtung dieses Hyperskripts schon haben.
	Denn die numerische Lösung der obigen Gleichung für beliebige Parameter ist kein großes Problem; wir können die Fermienergie jetzt also immer ausrechnen.
		Und wenn wir die Fermienergie haben, können wir sie benutzen um (ebenfalls numerisch) alle gewünschten Konzentrationen als Funktion aller vorgegebenen Parameter auszurechnen.
		Das tun wir mal - in einem eigenen Modul mit einem entsprechenden JAVA Applet, das die Numerik für uns übernimmt. Was man erhält sieht beispielsweise so aus:
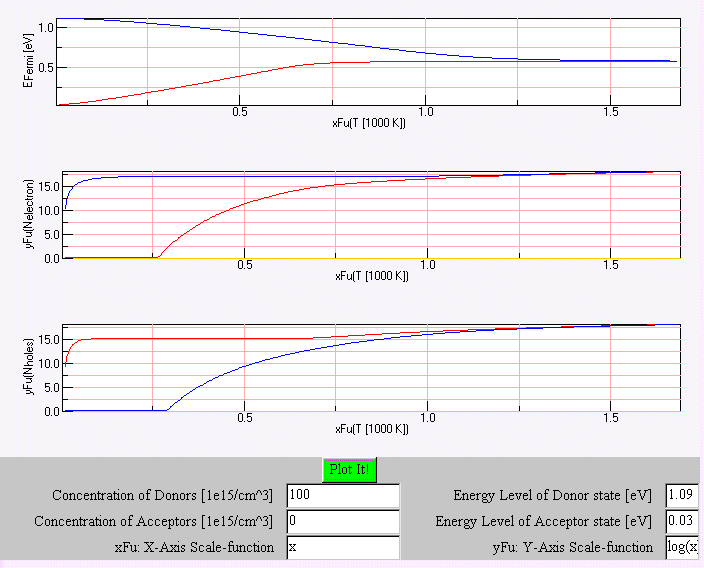
		Gezeigt ist: Die Fermienergie als Funktion der Temperatur (obere Kurve) Der log der Konzentration von Elektronen im Leitungsband als Funktion der Temperatur (mittlere Kurve). Der log der Konzentration von Löchern im Valenzband als Funktion der Temperatur (untere Kurve) für eine Konzentration an Akzeptoren von 1015 cm –3 mit den roten Linien, und für eine Konzentration an Donatoren von 1017 cm –3 mit den blauen Linien.
	Eigentlich ist damit alles gesagt. Da wir uns aber für prinzipielle Betrachtungen mit analytischen Formeln viel leichter tun als mit der Numerik, wird sich das nächste Unterkapitel mit einigen sehr nützlichen analytischen Formeln für die Ladungsträgerkonzentrationen beschäftigen.
		Fragebogen / Questionaire Multiple Choice Fragen zu 5.2.3

© H. Föll (MaWi 2 Skript)