 |
In den Kapiteln 2.1.1 und
2.1.2 wird im Grunde eine einfache Botschaft "kompliziert"
vermittelt. Hier schauen wir uns das Ganze nochmal in den großen Zügen an. |
 |
Zunächst geht es um Geschwindigkeiten und "Fließen". Die
wesentlichen Punkte sind: |
|
 |
- Frei bewegliche Teilchen in einem Material das im thermodynamische Gleichgewicht nur so "rumliegt" - Atome,
Elektronen, was auch immer - rennen mit "thermischer" Geschwindigkeit wild durcheinander, bleiben aber im Mittel
wo sie sind (Fliegenschwarmanalogie).
- Die "thermische" Geschwindigkeit v (aus ½mv2 = 3/2 kT) ist
schon klassisch bei Raumtemperatur "erstaunlich" hoch. Für Elektronen müssen wir hier noch eine quantenmechanische
Korrektur (später) einbauen; die grundsätzlichen Überlegungen sind davon jedoch nicht betroffen.
- Teilchenströme treten auf, wenn sich der ungeordneten Bewegung eine gerichtete
Bewegung überlagert. Dann "fließt" das ganze Ensemble mit einer Driftgeschwindigkeit
vD in Fließrichtung.
- Die Driftgeschwindigkeit ist dem Betrag nach i.d.R. sehr viel kleiner als die thermische Geschwindigkeit. Trotzdem ist
nur die Driftgeschwindigkeit für z. B. elektrischen Stromfluss verantwortlich.
|
 |
Damit kann man jeden beliebigen Teilchenfluß jT
= Flussdichte = Nettozahl der Teilchen die pro Sekunde durch eine Querschnittsfläche
A fließen = Fluß in eine Richtung – Fluß in Gegenrichtung = n · vD
schon hinreichend beschreiben; n ist dabei die Teilchendichte oder -konzentration, also die Teilchenzahl pro cm3. |
|
 |
Eine elektrische Stromdichte j ist nichts anderes als ein Strom elektrisch geladener
Teilchen, d. h. die (Netto)zahl an Ladungen, die pro Sekunde durch eine Querschnittsfläche A fließen:
wir haben j = q ·jT mit q = Ladung der Teilchen (i.d.R. eine (oder einige
wenige) Elementarladungen e). |
 |
Flüsse haben immer eine Ursache, eine "treibende Kraft" |
|
 |
Bei elektrischen "Flüssen" = Strömen ist die übliche Ursache ein
elektrisches Feld
E, das auf die geladenen Teilchen eine Kraft F = q · E ausübt und die Teilchen
damit in Feldrichtung beschleunigt. |
|
 |
Eine andere Ursache für Teilchenströme, die wir schon früher behandelt haben,
ist ein Konzentrationsgradient
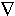 n.
Damit ist nach dem 1. Fickschen Gesetz, das wir atomar begründet haben, ein Teichenstrom jT
= – D · n.
Damit ist nach dem 1. Fickschen Gesetz, das wir atomar begründet haben, ein Teichenstrom jT
= – D · 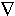 n gegeben. Das 1. Ficksche Gesetz gilt auch für geladene Teilchen - ein Konzentrationsgradient
"treibt" dann einen elektrischen Diffusionstrom. n gegeben. Das 1. Ficksche Gesetz gilt auch für geladene Teilchen - ein Konzentrationsgradient
"treibt" dann einen elektrischen Diffusionstrom. |
|
 |
Das gilt auch noch wenn wir für Elektronen das Ganze "richtig", d.h. quantenmechanisch
betrachten. |
 |
Schauen wir zunächst auf ein elektrisches Feld als treibende Kraft, die dann
"Feldströme" verursacht: |
|
 |
Damit sich eine feldverursachte konstante Driftgeschwindigkeit
vD ergibt, die bei Gültigkeit des Ohmschen Gesetzes proportional zu E sein muss, brauchen
wir zwingend eine Art "Reibung". |
 |
Klassische Reibung kann es aber im Atomaren nicht geben, stattdessen haben wir
den elementaren Prozeß der Energiedissipation
durch Stoßprozesse. Das sind die Prozesse, die immer für die "Thermalisierung"
verantwortlich sind, d.h. für die Tatsache, dass alle Teilchen sich im thermischen Gleichgewicht gleich verhalten -
eben mit der thermischen Geschwindigkeit "wild" durch die Gegend fliegen. |
|
 |
Unabhängig davon, mit was genau sich die Teilchen stoßen, kann man immer eine mittlere
Stoßzeit t = ½ mittlere Zeit zwischen zwei Stößen definieren, und
damit verbunden die mittlere freie Weglänge l = mittlerer zurückgelegter Weg zwischen zwei Stößen
= 2t(vT + vD). (Der Faktor ½ bzw. 2
ist hier historisch bedingt und bedeutungslos). |
|
 |
Alternativ kann man die "Stoßerei" in den Materialparameter Beweglichkeit
µ packen (der historisch gesehen früher "kam"); man erhält die Beziehungen |
| |
| µ | = | e · t
m | = | vD
E | = |
e · D
kT |
|
|
 |
Der letzte Term berücksichtigt, dass die früher behandelten Diffusionsprozesse,
die vom Material aus "gesehen" durch eine Diffusionskonstante D beschrieben wurden, auch nicht anderes
behandeln als Teilchen die mit "thermischer" Geschwindigkeit wild durcheinander rennen, "getrieben"
durch die thermische Energie kT. |
|
 |
Aus dieser mehr abstraken Sicht unterscheiden sich alle thermisch herumrennende Teilchen in
ihrem grundsätzlichen Verhalten nicht - man kann immer Stoßzeiten, mittlere freie Weglängen, und damit eine
Beweglichkeit definieren. |
|
 |
Damit kann es keine zwei unabhängige Materialparameter - µ und D
- geben; die beiden müssen verknüpft sein. Die Verknüpfung (per obige Gleichung ) ist elementar wichtig;
sie heißt nach den "Entdeckern" (oder
"Erfindern"?) Einstein-Smoluchowski Beziehung. Mehr dazu im Link. |
 |
Wenn man das alles verdaut hat, hat man erst mal einen sehr tief gehenden Einblick
in das Wesen der Materie gemacht. Außerdem hat man eine fundamentale Beziehungen für die elementare Eigenschaft
"spezifische Leitfähigkeit" s erhalten: |
| |
|
|
 |
In Worten: Will ich s optimieren, kann ich an zwei "Knöpfen"
drehen: - Konzentration der beweglichen Ladungsträger.
- Beweglichkeit der Ladungsträger
. |
|
 |
Wie "dreht" man an diesen Knöpfen? Richtig! - Arbeite mit Defekten im Kristall.
Wenn man das in Vollendung tut, nennt man es dann z. B. Halbleitertechnologie. |
| |
|
© H. Föll (MaWi 2 Skript)