Beziehung zwischen E-Modul und Schermodul

	Wie kann man die durch reine Scherspannung erzeugte Verformung durch reine Normalspannungen erhalten? Falls wir einen Weg finden, bekommen wir automatisch eine Beziehung zwischen Schermodul G und Elastizitätsmodul E.
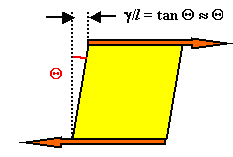
				Die Ausgangslage ist links gezeigt. Die reine Scherspannung verformt ein Quadrat in ein Raute.
				Wir können exakt die gleiche Verformung auch anders erhalten. Dazu betten wir gedanklich unser Quadrat (oder dreidimensional unseren Würfel) in ein identisches Material ein wie unten gezeigt.
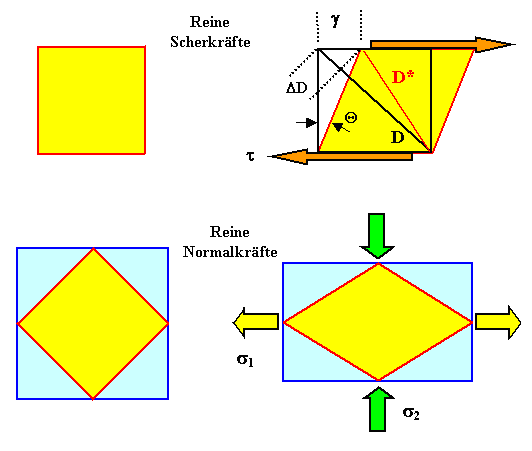
	Oben die Verformung mit reinen Scherkräften, unten exakt die gleiche Verformung mit reinen Normalkräften - nach Drehung um 45o und "Einbettung".
		Das klappt offenbar - wir erhalten dieselbe Verformung. Nun wollen wir damit den Schermodul berechnen.
	Der Schermodul war definiert als G = t/Q.
		Wir können das auch über die Änderung der Diagonalen DD = D – D* ausdrücken, da g2 = 2DD2, gilt g = 2½ · DD.
		Damit kann man Q wie folgt ausdrücken:
		Q  =   g l  =   2½ · 2½ · DD D  =  2 · DD D
		l ist die Länge des inneren Würfels; für kleine Winkel (die wir hier immer voraussetzen) gilt l » 2½D .
	Was bekommen wir mit den Normalspannungen s?
		Die erste Verformung mit nur s1 gibt eine Längenänderung der Diagonalen (Querkontraktion bei der zweiten Diagonalen beachten)
		D(1)D1 D1  =  e (1)1  =   s1 E D(1)D2 D2  =  e (1)2  =   – n · e (1)1   =  – n · s1 E
	Wird jetzt die zweite Verformung mit s2 überlagert, erhalten wir den zweiten Satz and Dehnungen.
		D(2)D2 D2  =  e (2)2  =   s2 E D(2)D1 D1  =  – n · e (2)2  =  + n · s2 E
	Solange die Dehnungen klein sind, dürfen wir sie linear überlagern, und erhalten
		DD1 D1 = D(1)D1 + D(2)D1 D1 = s1 + n · s2 E DD2 D2 = D(1)D2 + D(2)D2 D2 = – s2 + n · s1 E
	Da die beiden Diagonalen entgegengesetzt gleichgroße Längenänderungen erfahren müssen, erhalten wir als erstes Resultat |s1| = |s2| .
		Die Scherkräfte auf die Flächen des gelben Quadrats bzw Würfels sind damit
		Ft  =  ½ ·2 · 2–½s · Ablau  =  2–½s · Ablau
		da jede der jeweils 2 wirkenden Kräfte eine Komponente 2–½ in der gelben Ebene hat und dort zur Hälfte wirkt; Ablau ist die Fläche des blauen Würfels.
		Die Fläche des gelben Würfels ist Agelb = 2–½ · Ablau, damit erhalten wir für die Scherspannungen
		t  =   Ft Agelb  =  s
	Einsetzen von s = t in die DD/D Formel und umschreiben auf Q ergibt
		DD D  =   s(1 + n) E  =   t(1 + n) E = Q 2
	Als Endergebnis erhalten wir
		t  =   E 2 · (1 + n) · Q
		Das ist die im Skript gegebene Formel, falls wir den Schermodul G definieren als
		G  =  E 2 · (1 + n)
	Diese Umrechnung ist natürlich nur eine Art indirekte Hauptachsentransformation. Eine Rotation des Koordinatensystems um 45o hätte genau die richtige Spannungsverteilung gezeitigt; siehe den entsprechenden Modul.

Mit Frame

7.1.3 Elastische Moduln

Transformation einer reinen Scherung auf Normalspannungen

© H. Föll (MaWi 1 Skript)