| |
Free Enthalpy of Reduction Processes |
 |
Free enthalpy
is just a fancy word for a particular kind of energy. The "free enthalpy of reduction" is a number that tells
you how much energy it takes to rip some metal oxide apart into the pure metal and some oxygen.
It takes
reduction energy to rip an oxide apart and we assign a plus sign to that: MO + energy
--> M + O. This necessitates that when you form that oxide from its constituents, you gain
exactly this energy, now called formation energy and written with a minus sign: M + O – energy --> MO
|
|
 |
Let's look at a system of isolated oxygen and metal atoms at some temperature.
It contains the usual thermal energy that is contained in the motion of the atoms and
chemical energy, a kind of potential energy that can be gained by the possible chemical reactions that have no yet occured.
Now let the atoms react to form an oxide. The system will have to have the same total
energy (energy is conserved, after all) but the chemical energy as been released and turned into thermal energy - the system
is hotter now. Let some hydrogen and oxygen react in a closed container to hydrogen oxide, commonly called water, and it
will be considerably hotter in there!
In other words: the total energy hasn't changed but the temperature has, and so
has the entropy, the degree of disorder
in the system. A bunch of atoms running about like crazy in a hot gas is just more disorderly than a solid crystalline oxide
with every atom in its place. You can't get much more orderly than that. |
|
 |
Now a rather important universal
law, somewhat simplified for the case here (let's call it the "law of compromises"), states two things:
- Reducing your potential energy is good, but reducing your entropy,
i.e. getting more orderly, is bad.
- You must balance both parameters, finding the best compromise between low energy
and high entropy, and you must pay more attention to the entropy at high temperatures.
Compromising means that you do not go for gaining all the formation energy but for a "compromise energy"
that is somewhat smaller, leaving "room" for still having a good amount of entropy. This "compromise energy"
is called free enthalpy. |
 |
Now we can look a the graph below. It plots the "free enthalpy" (= compromise
energy) for the formation / dissolution of various oxides as a function of temperature. |
| | |
| |
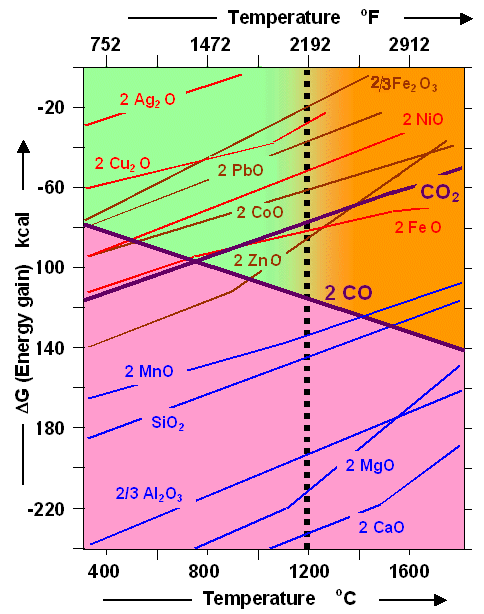 |
| Energy gains / losses in forming / dissolving oxides as a function of temperature |
| Large-scale detailed diagram here |
|
| | |
|
 |
To get an idea of what is shown let's look at the top-most red line labeled "2
Ag2O". It starts at an energy value of –28 kcal ("kilo calories", an old-fashioned unit
for energy (1 kcal = 4187 J). What it means is that forminmg 2 molecules of silver oxide at 400 oC from silver
and oxygen atoms / molecules, you gain 28 kcal relative to the energy the constituents
had before the reaction. Alternatively, you need -28 kcal to break the oxide apart.
Don't
worry about the minus sign, the "2" or whatever number you find for the other substances - it is only there to
enable a direct comparison; I'll get to that in a moment. |
|
 |
First, however, we notice that the 2 Ag2O and all other lines except
one always go "up" with increasing temperature. That means that the energy gain gets less if the reaction
happens at higher temperatures. For 2 Ag2O at 800 oC we have only half of the 400 oC
value.
The reason is clear. The reaction lowers the entropy! After the reaction you have fewer molecules in your system,
they all are the same, and heavier - and you just can't make as much disorder with them than with the larger and mixed crowd
you had before. Consider a crowd of 200 little boys and girls, lustily running around, and compare that with 100 sullen
unisex teenagers (with the same total weight) hanging around more or less immobilized. Where would you expect more disorder?
This unwanted lowering of the entropy by the reaction counts more at high temperatures and the "compromise energy"
or free enthalpy must become smaller as a consequence. You "pay" more in terms of energy for loosing all that
entropy. |
 |
Now you need to look a the situation from the viewpoint of an oxygen atom. It
likes to react with almost everything because there is almost always a gain in its "chemical" energy. Give it
some silver and it forms silver oxide. Give it iron, copper, carbon, ... and it forms iron, copper, carbon, ...oxides. |
|
 |
Now give it all of these elements simultaneously.
Now you need to answer two questions: - What kind of oxide will I get in this case?
- What if there is more than one oxide for one kind of "customer"; e.g. carbon monoxide (CO) and carbon dioxide
(CO2)? What will be formed?
|
 |
Easy. The "second
law" will tell. And its answer can be condensed into the graph above. All other things being equal (and
that necessitates to come up with numbers like "1", "2", "2/3" in front of the chemical symbols),
you will get the oxide with the "lowest" free enthalpy at the temperature selected, i.e. the largest
number without the minus sign 1). Offer all the elements showing up in the graph
and you would end up with CaO at any temperature. |
 |
Now let's look at the "joker" in this graph, the carbon
monoxide line! It is the only one that goes "down", meaning that it takes more
energy to rip the CO molecule apart at high temperatures compared to lower ones. The reason for this aberrant behavior is
that the entropy actually increases when carbon monoxide (CO) is formed! It stays gaseous
and thus unordered in contrast to most other oxides. That is also true for the formation of carbon dioxide (CO2).
But here you get only one gas molecule when reacting one O2 (gas) molecule
with (solid) carbon, keeping the number of gas molecules constant, while you get two
(gas) CO molecules by using up one O2 (gas) molecule. The reaction increases the number of gas molecules, and
thus produces a far more disorderly situation! |
|
 |
The rest is easy. As the temperature goes up, the formation of carbon monoxide becomes more
and more favorable compared to the formation of, for example, silver, (Ag), copper (Cu), lead (Pb), cobalt (Co), or zinc
(Zn) oxides and even carbon dioxide (CO2).
The temperature where an oxide line crosses the CO line is the
temperature where the reduction begins, i.e. the oxygen would now prefer to "defect" from the metal atom to a
carbon atom, producing carbon monoxide. It doesn't do that directly or literally - after all reduction occurs because CO
is oxidized to CO2 and then gets reduced again to CO - but here we only look at the net energy balance after
all is done, and it doesn't matter how it was done, and how many intermediate steps were needed.. |
 |
The graph tells you that you can reduce those oxides with carbon that have parts
of their oxide curve above the CO curve. The crossing of the two curves defines the
temperature where the reductions reaction can start. This includes all the oxides in the green and orange region of the
graph.
There are more metal oxides that can be reduced by carbon (monoxide), for example nickel (Ni) or tin (Sn) oxide.
Their curve would also be in the "right" green and orange area, but they and many others have been omitted for
clarity. |
|
 |
However, there are also plenty of oxides, like Calcium (Ca) or magnesium (Mg) oxides (and
more not shown) that are always below the CO curve. These are the "difficult to smelt metals mentioned long ago, occupying
the region colored violet, the color of despair. There is simply no way to reduce those oxides
with carbon. |
 |
Finally we have oxides like silicon (Si) dioxide or manganese (Mn) oxide that
do cross the carbon monoxide line - but at rather high temperatures! |
|
 |
Assuming that 1 200 oC is about the limit of what could be reached in the reduction
zone of an old-fashioned smelter in ancient times, a region always a bit colder then the actual "burning" zone,
the green and orange regions divide chemically and technically possible smelting with
carbon (green region) from smelting that is chemically possible but technically out of reach
(orange region). |
| |
| |
© H. Föll (Iron, Steel and Swords script)
