| | |
 |
I'm sure you know the difference between hot and cold water. If not, stir your iced drink and your boiling soup a while with your finger and you shall
know. You probably also know the difference between a cold piece of iron an a hot one. If not, just touch the exhaust pipe
of your car after you went for a long ride. |
|
 |
It's easy to know if an inanimate object is hot or cold. You find out by touching
it. With animated objects it might be more difficult. How hot is that lady over there? Finding out by touching might not
be such a good idea. |
|
 |
How about measuring "hotness" or
"coldness"? That means to put a number on coldness and hotness and call it temperature.
Typically you must now touch the object with some device that gives you a response on some scale.
You now have two problems: - What kind of device could do that?
- What kind of scale should I choose?
Despite appearances, the two problems are completely unconnected. That becomes clear immediately if you look at the
simplest device for measuring temperature: the good old mercury (Hg) thermometer. Mercury (or other liquids like alcohol)
expand when becoming hot, and the top of a column of the stuff contained in a thin glass capillary will climb up if the temperature goes up.
|
|
 |
OK, we solved the first problem. We now have
some device that responds to temperature by moving a "pointer" (the top of the column) up and down a scale.
But what kind of number do I put on the scale next to the capillary? Is there some universal
principle that I can use for guidance?
Yes there is. For questions like this, the universal principle is: |
| |
|
|
|
Ask your friendly Materials Scientist
|
|
| |
|
|
 |
In this case she will weasel a bit. She might mumble that the best way would
be to express temperature in terms of energy, but that you won't get this, and that
the next best thing would be to use the so-called absolute temperature scale, which
gives temperatures in "Kelvin (K)". It's just Kelvin, not "degree Kelvin"; no oK.
However, if you press her a bit, she will admit that in everyday life she actually uses centigrades (oC),
degree Fahrenheits (oF) or whatever else she grew up with (if she is of French origin it might be Réaumur
(oR) but we won't hold that against her). |
| |
| |
| |
|
| | |
|
|
 |
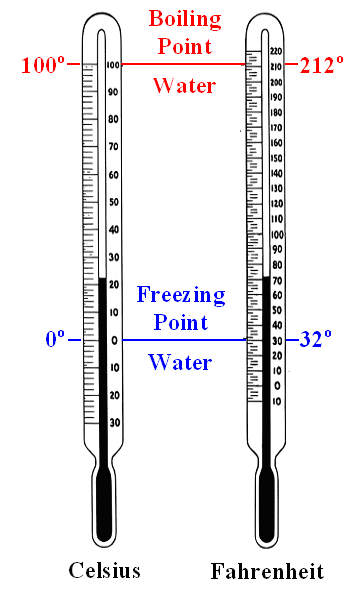
Both thermometers measure the same thing
("temperature") but with different scales: degree Celsius or degree Fahrenheit. |
 |
The guys who invented the first thermometers (there were only guys, female scientists
hadn't been invented or discovered yet) had different ideas
about how to fix a scale. |
|
 |
The Swedish astronomer Anders Celsius
in 1742 assigned 0 °C to the freezing point of water and 100
°C to the boiling point. In between the scale was subdivided in 100 parts
(defining a temperature difference of 1 °C), which allows to extrapolate to temperatures above 100 °C and
below 0 °C. 1)
The Celsius scale is the scale almost everybody uses today (even
the French). |
|
 |
Daniel Gabriel Fahrenheit,
a German from Danzig, begged to differ in 1714. He picked as the zero point (0 °F) of his scale the low
temperature of the stiff winter 1708/1709 in Danzig (-17,8 °C on the Celsius scale), because he wanted to avoid negative
numbers. For rather obscure reasons 2) he took 32 °F for the freezing point of water,
which automatically leads to 96 °F as another fixed point for the body temperature of humans.
From a scientific
point of view the Fahrenheit scale is problematic because its fixed points are not well defined. From a practical point
of view it is a great scale because 0 °F - 100 °F defines about the extremes of temperature humans may experience.
You know that 0 °F is lousily cold and 100 °F is scaldingly hot.
Fahrenheit is still the official scale of
the United States, Thailand and Belize; in Canada it is retained as a secondary scale. The rest of humankind uses °C
or "centigrades". |
|
 |
René Antoine Ferchault de
Réaumur proposed a scale with 0 °R as the freezing point of water and 80 °R for the boiling
point. Why 80 and not 100 or 72,6 or whatever was a kind of mystery until I found the explanation. 3)
My own explanation was that the French have trouble counting beyond 20, and going up to 100 was just too challenging. 80,
in French is "quatre vingt", i.e. 4 times 20; 90 is "quatre-vingt-dix", i.e. 4 times 20 and 10. Counting
just gets too complicated above eighty. |
|
 |
There are several other scales, all but forgotten, and I won't go into this anymore. |
 |
Instead we give a look at the scientifically important Kelvin scale or absolute temperature scale. It rests on
the tremendous insight that there is a lowest temperature, a coldness that cannot be surpassed, a natural absolute zero point of temperature. You can't do better than that to define 0 K or
zero Kelvin. |
|
 |
Going up is done with intervals borrowed from the Celsius scale. A difference
of 10 K is the same difference between some two temperatures as 10 oC difference.
There is no particular reason for using Celsius, except that it was convenient for the majority of scientists who were
used to the Celsius scale by their upbringing. |
|
 |
The Kelvin scale is so important in science because absolute
temperature measured in Kelvin (and then always abbreviated T) can go right into equations and formulae.
|
|
 |
Here is a conversion diagram for the four scales discussed: |
| |
|
|
|
|
| | |
|
 |
I must now discuss all those questions that accumulated in the back of your mind.
Let's bring them out:
- How do we measure temperatures outside the range of common thermometers? If it's
too cold, the liquids in the capillary will freeze; if it's too hot, they evaporate or the capillary melts. When we forge
iron and steel it needs to be pretty hot and you have never seen a smith sticking a thermometer into his hearth.
- Why does mercury (Hg) or just about everything expand more or less
when it gets hotter?
- What is temperature, anyway? After all, if you look closely—very closely—
at a piece of hot or cold water, you "see" those little things, whatchamacallit?", those water
molecules (H2O). There is a certain (large) number in a liter of water, and heating
or cooling does not change that number nor the molecules. Same thing for hot or cold
steel, except that instead of molecules you now see mostly iron atoms. Same thing for simply
anything.
The questions thus is: what's the difference between the hot
or cold molecules or atoms that form the material you are contemplating?
I bet you weren't quite aware that those questions were at the back of your mind. Now you are—and I must answer
them. |
 |
1. How do we measure (extreme)
temperatures? There are many ways; we will only give some of them a quick glance. |
|
 |
Most simple and wide spread is the use of a resistor
that changes its electrical resistivity in a well defined way with temperature. Platinum (in a thin layer, so you only need
tiny amounts) does just that. And no, I won't go into why Pt (and just about everything else) changes its resistivity with
temperature.
That's great because this allows you to generate an electrical signal,
that can be processed directly by the "electronics inside" that run about everything today. Platinum is also a
great material for this because it will not corrode and can take high temperatures because its melting point is 1.772 oC
(3.222 oF) |
|
 |
Quite simple and widespread are also "thermocouples",
a junction between two different materials. If that junction is at a temperature different from that of the rest of the
material, a voltage develops that is indicative of the temperature (difference) and that you can easily measure with a voltmeter.
An no, once more, I will not even try to attempt to explain why that happens.
Thermocouples are widely used at high
temperatures and when precision counts. |
|
 |
What are we going to do at really high temperatures,
when pretty much everything would be molten? Easy. We look at the light emanating from
all hot bodies.
What you and just about everybody else knows is that hot things
start to glow. Increasing the temperature of a piece of steel changes its color from dark red, via cherry red, orange, yellow
to white (and eventually blue if it wouldn't melt before that happens).
So by measuring precisely
what kind of color (more precisely: spectrum) a hot piece of iron assumes, we can compute it's temperature.
What you
probably don't know is that the composition of the light (the spectrum) that hot bodies emit is the same
for all hot bodies. This includes your hot body, the sun, everything. If I would heat
you up to 1.000 oC (1.832 oF), you would glow exactly like a piece
of iron or whatever. I admit that heating you up that much in air would induce some changes in your body (described as "burning"
or "oxidation") that are not enjoyable as we know from many experiments performed by the church a few hundred
years ago. So we heat you up in an oxygen-free environment (not enjoyable either) and glow you will. |
 |
It was Max Planck in
1900 who discovered the universal law of "black body" radiation (no, he wasn't thinking of your body after the
experiment described above). His famous equations not only fits the observations very well and and allows us to measure
temperature by just "looking" at an object with a spectrometer, it opened the door to quantum
theory. |
|
 |
In fact, the glowing of hot objects in "colors" that betray their temperature
can only be understood by quantum theory. We have a first little indication here that
quantum theory is not just something physicists amuse themselves with when dealing with exotic things that have nothing
to do with everyday life. Just the opposite.
Whenever a smith looks at his hot piece of steel to judge by its color
if its temperature is right, he is doing quantum theory, probably without knowing that. |
 |
We have two questions left. But I stop here. After
all, this is a "BASIC" module. |
|
 |
I will, however, take up those questions at some other parts of the hyperscript.
If you make it that far, you will learn that knowing the answer to question three is absolutely essential for understanding
how to make good swords. |
| |
| |
© H. Föll (Iron, Steel and Swords script)